Session 12 The Multiplication of Fractions Big Ideas

Session 12: The Multiplication of Fractions Big Ideas Instructional opportunities for students should foster both conceptual understanding of multiplication and division across a range of contextual situations and procedural fluency built upon understanding. Understanding of and fluency with multiplication and division of fractions should be built upon an understanding of fractions as numbers, visual models, unit fraction understanding, the meaning of the operations, and the properties of operations. Petit et al, 2016) © 2018 OGAPMath LLC. For non-commercial use only. 1

Build Fluency with Understanding • Multiplication and division of fractions are among the most complicated fractions concepts that elementary students encounter (Fendel, as cited in Tirosh, 2000). • Instructional opportunities that students encounter should consider the meaning of multiplication and division in a range of situations and build procedural fluency with understanding (Kieren, as cited in Huinker, 2002; Aksu, 1997). © 2018 OGAPMath LLC. For non-commercial use only. 2
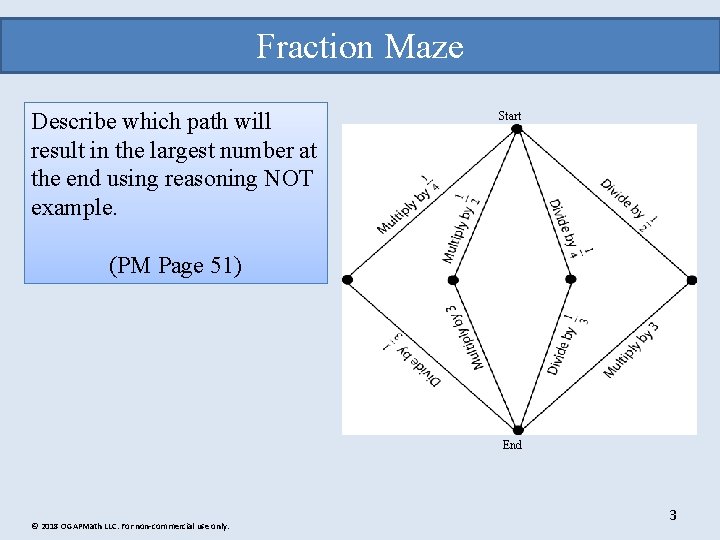
Fraction Maze Describe which path will result in the largest number at the end using reasoning NOT example. Start (PM Page 51) End © 2018 OGAPMath LLC. For non-commercial use only. 3

Review the questions and student work in Figures 10. 1, 10. 7, and 10. 9 (Pages 166 -171) (Petit et al, 2016) • What did you notice about the design of the questions? • At what level of the OGAP Fraction Progression is the evidence in each student response? © 2018 OGAPMath LLC. For non-commercial use only. 4

Read Page 166 -167 Begin at bottom of 167 (“One must not overgeneralize …) and end at middle of Page 168 (Impact of Division by a Fraction). © 2018 OGAPMath LLC. For non-commercial use only. 5

Solve each of the following problems. Represent the solution with a model. 1) A 4 th grade class is making a design. Each design needs ⅗ yard of ribbon. If the class is making 10 designs how many yards of ribbon do they need? (Grade 4) 2) A rubber band is ¾ inch long. When fully stretched it is 5 times as long. How long is the rubber band after it is fully stretch? (Grade 4) 3) A recipe calls for 1 ⅔ cup of flour. How many cups of flour is ½ of the amount needed for the recipe? (Grade 5) 4) Three-fifth of the students in fifth grade at Oz Elementary School have brown eyes. There are 125 students in the fifth grade at Oz Elementary School. How many student have brown eyes in the fifth grade at Oz Elementary School? (Grade 5) © 2018 OGAPMath LLC. For non-commercial use only. 6

Questions ① How are the problems alike and/or different? ② How did the context of the problem influence (or not) the model you used to represent the solution? © 2018 OGAPMath LLC. For non-commercial use only. 7

Developing a Multiplication Algorithm with Meaning Students may struggle with the use and understanding of formal algorithms when their knowledge is dependent primarily on memory, rather than anchored with a deeper understanding of the foundational concepts. (Kieren, as cited in Huinker, 2002) © 2018 OGAPMath LLC. For non-commercial use only. 8
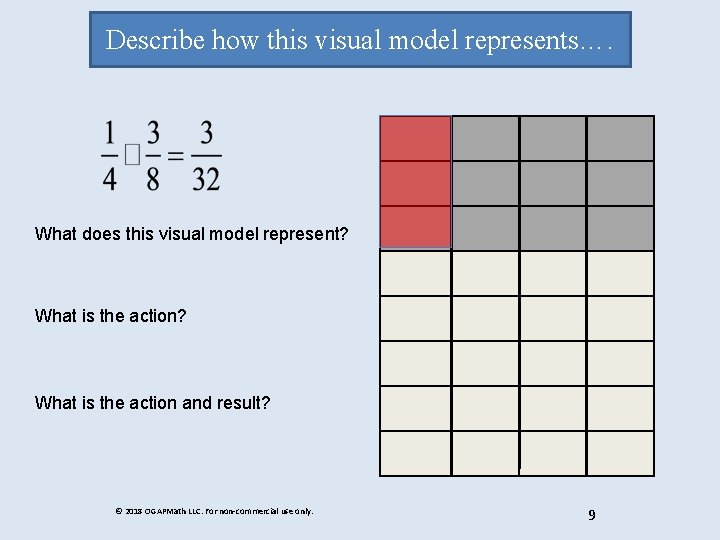
Describe how this visual model represents…. What does this visual model represent? What is the action and result? © 2018 OGAPMath LLC. For non-commercial use only. 9

Describe how this visual model represents…. What are the dimensions of the figure? How are the dimensions partitioned? What is the action? What is the result? . © 2018 OGAPMath LLC. For non-commercial use only
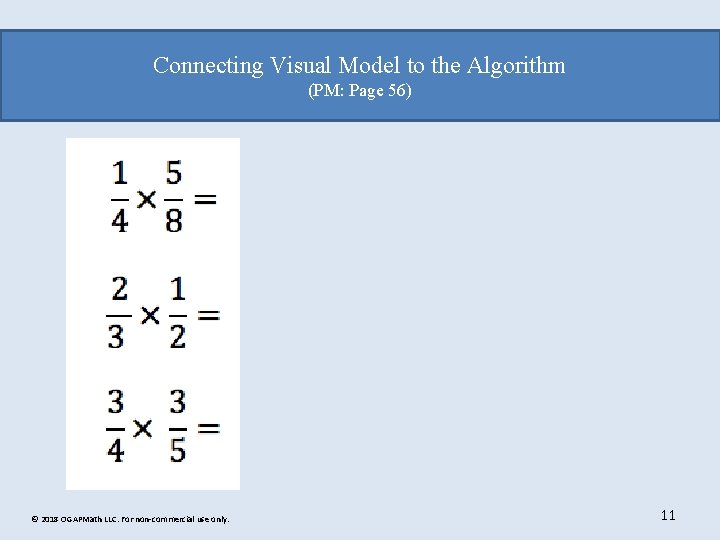
Connecting Visual Model to the Algorithm (PM: Page 56) © 2018 OGAPMath LLC. For non-commercial use only. 11
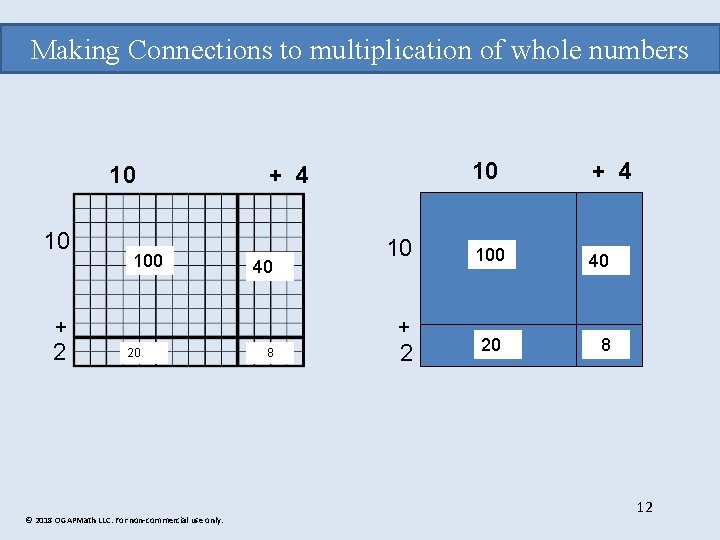
Making Connections to multiplication of whole numbers 10 10 100 40 + 2 10 + 4 10 + 20 © 2018 OGAPMath LLC. For non-commercial use only. 8 2 + 4 1010 44 100 40 20 8 12
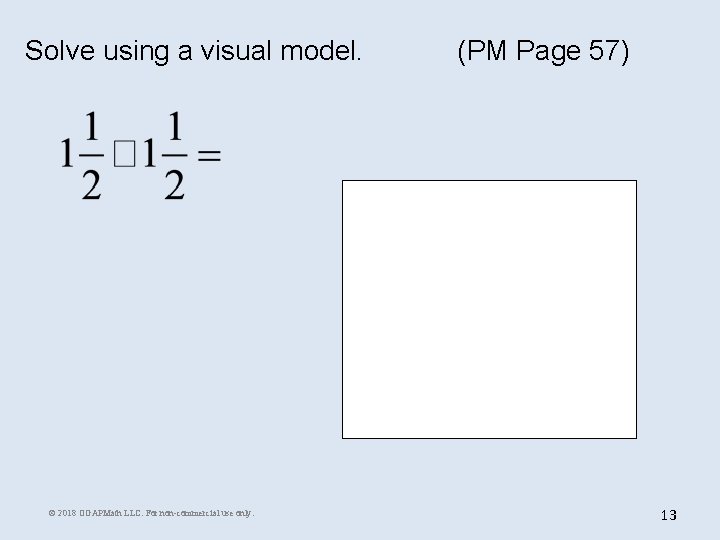
Solve using a visual model. © 2018 OGAPMath LLC. For non-commercial use only. (PM Page 57) 13
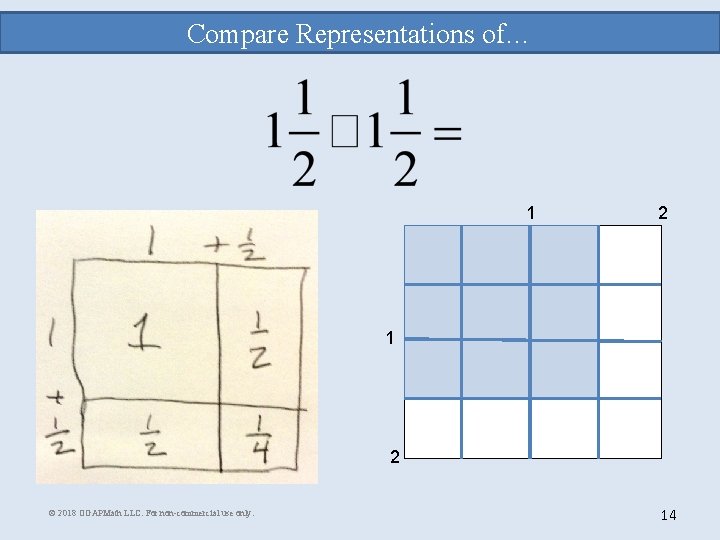
Compare Representations of… 1 2 © 2018 OGAPMath LLC. For non-commercial use only. 14
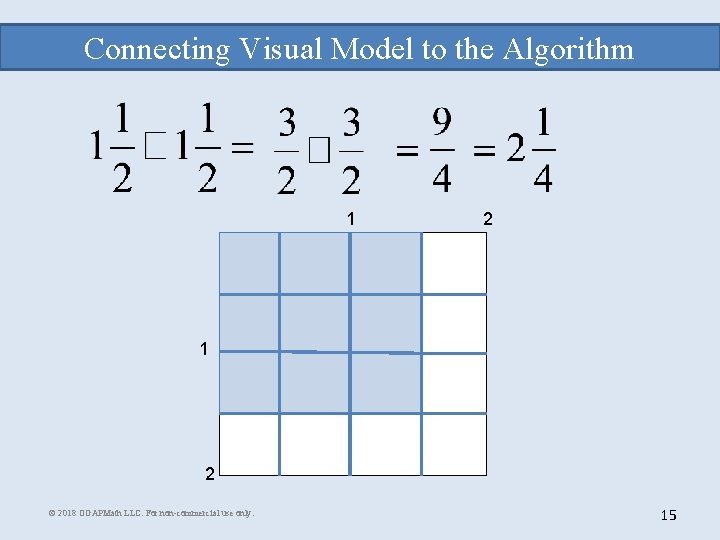
Connecting Visual Model to the Algorithm 1 2 © 2018 OGAPMath LLC. For non-commercial use only. 15

Using Visual Models to Solve Mixed Numbers (PM Page 59) Solve each problem using a visual model. Show the connections between the visual models and the algorithm for solving multiplication of mixed numbers. © 2018 OGAPMath LLC. For non-commercial use only. 16

Evidence in Student Work Select an Instructional Strategy based on the evidence across the class. (Inside Back Cover PM) © 2018 OGAPMath LLC. For non-commercial use only. 17

Math Program/Instructional Materials You will review your instructional materials paying careful attention to the 5 important areas regarding multiplication of fractions: • Use of visual models • Use of problem contexts • Use of estimation and magnitude reasoning • Use of unit fractions understanding • Use of properties of operations 1) What are the strengths of the multiplication unit in your curriculum? 2) Based on your new learning and your findings in your math program, what might be done to strengthen instruction? © 2018 OGAPMath LLC. For non-commercial use only. 18

OGAP Fraction Item Bank • Go to www. ogapmathllc. com • Go to “For OGAP Participating Teachers, Math Coaches, and Leaders” • Click on “Fractions” • Enter Password – 2018 FTevidence • Download File © 2018 OGAPMath LLC. For non-commercial use only. 19

Item Bank Scan ① With a partner briefly scan through the items. a) Describe a couple of ways that the problems vary in this section. ② Choose 1 item that you think will provide important information about your students understanding of multiplication of fractions. a) Be prepared to discuss the reasons why you selected the item. © 2018 OGAPMath LLC. For non-commercial use only. 20
- Slides: 20