Seriously Why is Negative time Negative Positive Reflections

Seriously… Why is Negative time Negative Positive? Reflections on a META Math Annotated Lesson Plan James Tanton MAA, Mathematician-at-Large

ABOUT THE MAA META MATH PROJECT Undergraduate mathematics courses often include example problems attending to applications in science, engineering, economics, business, …. • Display the utility of mathematics • Motivate the need for deep mathematical thinking • Point out career options for mathematicians META MATH works to add secondary mathematics teaching to the list of legitimate application areas of undergraduate mathematics. Easily-integrated curriculum materials that • Do the above, and • Illustrate the deep value of “looking back. ”

Your students have just completed a course on groups, rings and fields … Consider the ring of integers with the usual operations + and x. Could your students explain why …

THE FACT IS THAT …

An inadequate overview of humankind’s struggles with negative numbers … Based on: Bruce Meyers, Math Past for Eureka Math Leo Rogers, History of Negative Numbers, https: //nrich. maths. org Martha Smith, History of Negative Numbers, https: //web. stanford. edu/class/me 161/documents/History. Of. Negative. Numbers. pdf Florian Cajori, History of Mathematics, 1991 ~ 150 BCE: Chinese Counting Rods Positive and Negative quantities for accounting. The ancient Greeks were locked into a geometry mindset.

~ 250 CE Greece Acknowledged that some equations with give “absurd solutions. ” Leo Rogers, NRich

~ 850 CE Middle East Scholars aware of Brahmagupta’s work. Rejected negative numbers and went back to studying six different classes of quadratic equations. But some return to thinking of negative numbers in matters of profit and debt. Stated rules similar to Brahmagupta’s for addition and subtraction of quantities. ~ 1150 CE India Bhaskara acknowledges roots of negative quantities in solving quadratics, but comments not socially acceptable. ~ 1200 CE Europe Seems unclear to scholars if Fibonacci’s Liber Abaci attends to negative quantities. No explicit mention, but there are problems in it that lead to negative solutions, which are described as “debt. ”

~ 1400 – 1600 Europe Chuquet first to use negative numbers in a printed European work. Called them “absurd numbers. ” In the search for the quartic and cubic formulas, Cardano, Bombelli, et al, used negative quantities, but exhibited discomfort. (eg Cardano did not allow negative coefficients in his quadratic equations. ) Viete did not acknowledge negative numbers.

~ 1600 -1700 Europe Descartes showed that sometime “absurd solutions” to equations could be manipulated to yield positive solutions. Pascal rejected negative numbers. Wallis accepted them as “quantities larger than infinity, but not less than zero. ” Wallis drew the number line.

~ 1700 – 1800 Europe Leibniz argued that the arithmetic with negative numbers, despite philosophical objections, could still be valid. Maclaurin, in his Treatise of Algebra in Three Parts, regarded negative numbers just as valid as positive ones. Euler, in his Complete Introduction to Algebra, used debt and profit models to justify why negative times negative should be positive. But many philosophers objected to this mathematical thinking.

~ 1800 -1900 Europe Wessel, Argand, de Morgan, Peacock, Hamilton developed different representations of “imaginary numbers” and developed a systematic “logic” behind their arithmetic. A theoretical framework for negative numbers established. TODAY: Be clear on negative numbers by grade 7

I don’t mean to be flippant … Yes, we can teach negative numbers to students at an early age. Yes, students can become familiar with their mechanics and workings. Yet the story of human history shows that it takes a VERY LONG TIME to truly make sense of their meaning and nuance, to develop a deep internal understanding beyond familiarity.

UK National Lottery scratch ticket, 2007

I ASKED ON SOCIAL MEDIA … Is there a model for negative numbers which naturally illustrates within it the idea that negative times negative should be positive? But one model worked for me. Issues: 1. Awfully specialized circumstance. 2. The definition of multiplication is asymmetrical.

The META MATH Annotated Lesson Plan It’s got to go back to a establishing a “systematic logic, ” a la the work of the 1800 s, a la the work of an abstract algebra course. From the Pre-Activity Assignment:

In the world of counting numbers, multiplication manifests itself as “repeated addition. ” Is it philosophically obvious that 4 x 5, “four groups of five, ” should give the same answer as 5 x 4, “five groups of four”?

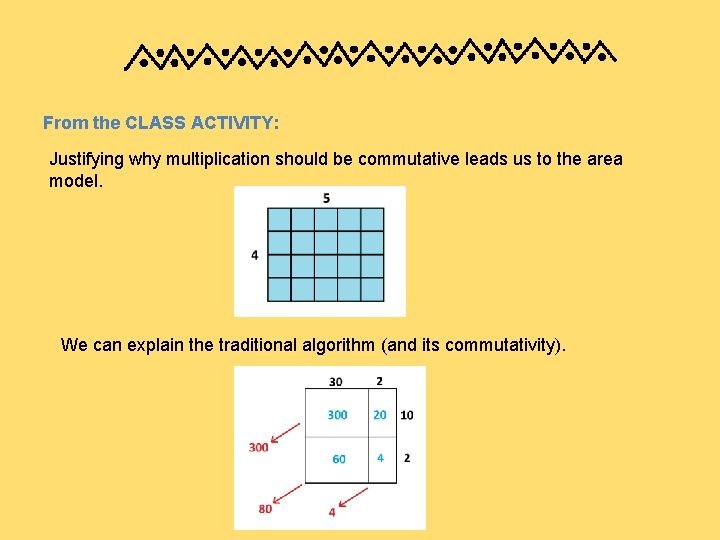
From the CLASS ACTIVITY: Justifying why multiplication should be commutative leads us to the area model. We can explain the traditional algorithm (and its commutativity).

Something curious …

DECLARING WHAT WE CHOOSE TO BELIEVE We’re at the point that we choose to believe the following “facts” of arithmetic, at least, in the world of counting numbers. QUESTION: Do these three rules feel so “natural” and so “right” that you think they should hold for ALL numbers, not just the counting numbers?

If you choose to answer YES, then there are consequences.

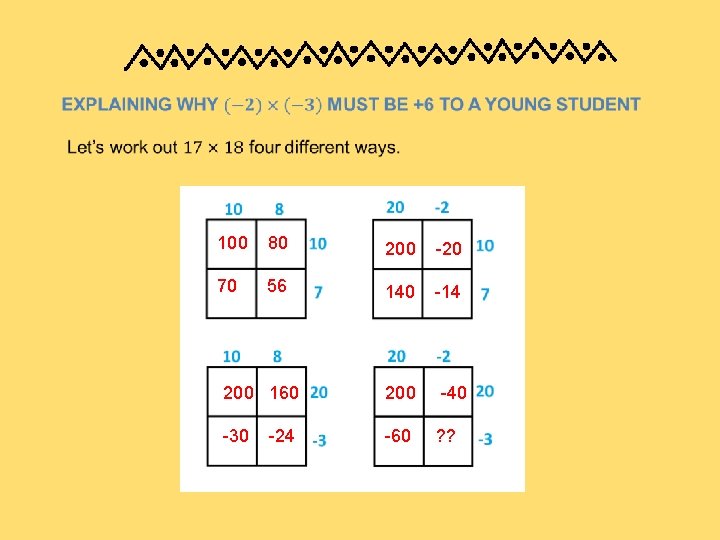
100 80 200 -20 70 56 140 -14 200 160 200 -40 -30 -60 ? ? -24

THE FORMAL APPROACH

FOR COMPLETENESS … The discussion in the classroom work point out that we are assuming additive inverses are unique. This is addressed in the homework exercises.

The annotated lesson plan works to hit hard on … • the challenging nuance and subtlety of negative numbers • the interplay between natural student/human thinking and axiomatic work • the philosophical work that leads to that axiomatic work And, moreover … • Providing the mental space for metacognition and deep internal understanding.

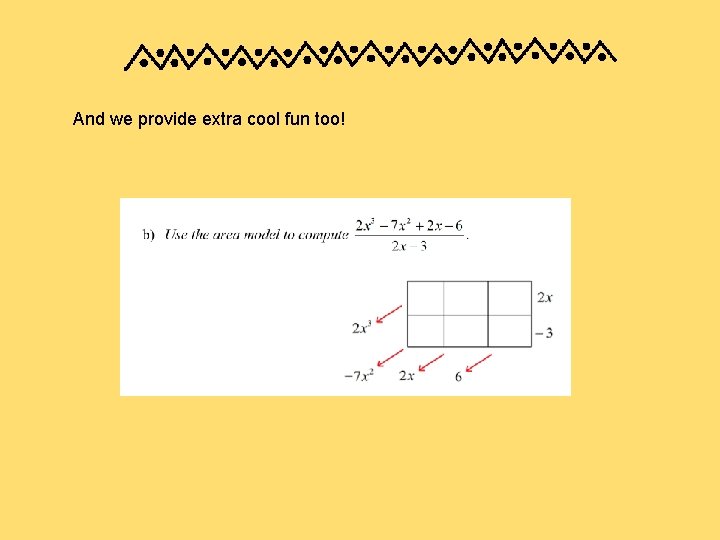
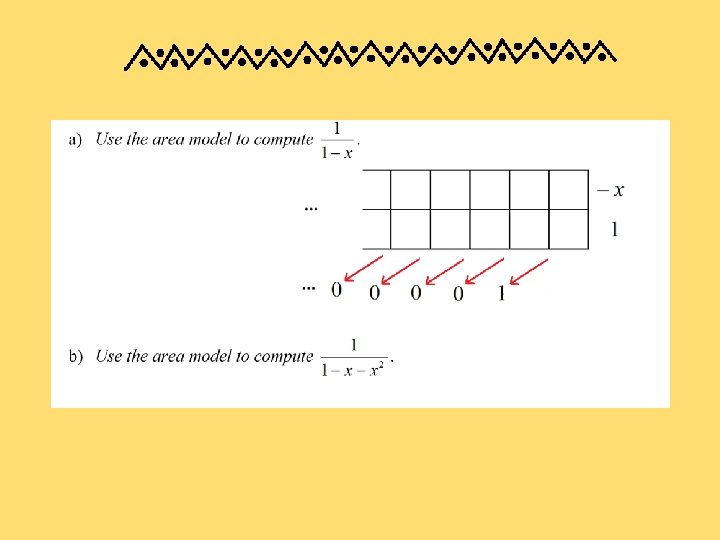
And we provide extra cool fun too!

If you would like to see the (unofficial) annotated lesson plan, it’s (secretly) here: jamestanton. com/? p=2315

THANK YOU! JAMES TANTON tanton. math@gmail. com jamestanton. com/? p=2315