Sequential Systems with Random Inputs Introduction Examples Lift

Sequential Systems with Random Inputs Introduction • Examples: Lift control systems, alarm systems. • In these systems, inputs, i. e. from sensors, limit switches, pushbuttons, etc, may be completely random and can come at any time and in any order. • Huffman Method can be readily employed for the design of such systems. • In designing such systems, all possible/feasible input combinations will need to be taken into account. IA – System with Random Inputs 1

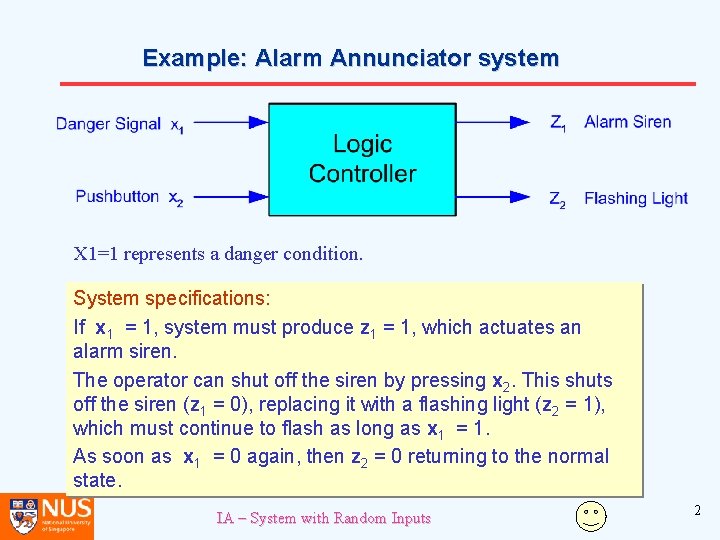
Example: Alarm Annunciator system X 1=1 represents a danger condition. System specifications: If x 1 = 1, system must produce z 1 = 1, which actuates an alarm siren. The operator can shut off the siren by pressing x 2. This shuts off the siren (z 1 = 0), replacing it with a flashing light (z 2 = 1), which must continue to flash as long as x 1 = 1. As soon as x 1 = 0 again, then z 2 = 0 returning to the normal state. IA – System with Random Inputs 2

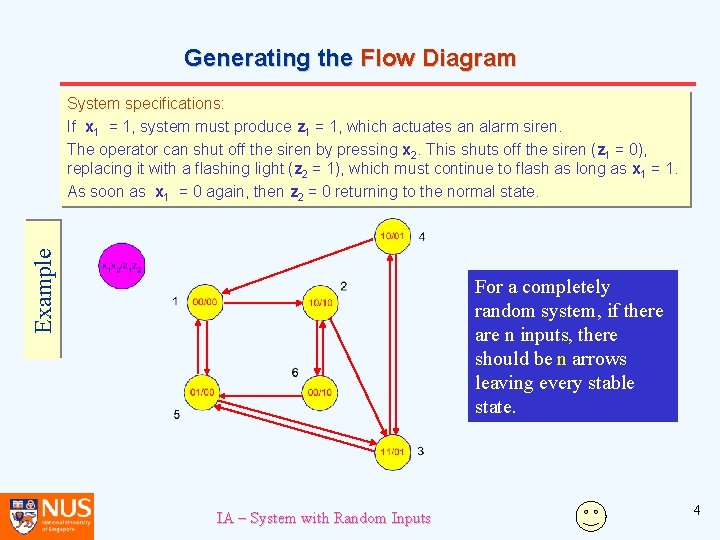
Generating the Flow Diagram • The first step in the design is to draw the flow diagram. • In the Flow Diagram, the convention is to use a circle to represent a stable state, with inputs on the left separated from outputs on the right by a slash. • Example: X 1 X 2/Z 1 Z 2 IA – System with Random Inputs 3

Generating the Flow Diagram Example System specifications: If x 1 = 1, system must produce z 1 = 1, which actuates an alarm siren. The operator can shut off the siren by pressing x 2. This shuts off the siren (z 1 = 0), replacing it with a flashing light (z 2 = 1), which must continue to flash as long as x 1 = 1. As soon as x 1 = 0 again, then z 2 = 0 returning to the normal state. For a completely random system, if there are n inputs, there should be n arrows leaving every stable state. IA – System with Random Inputs 4

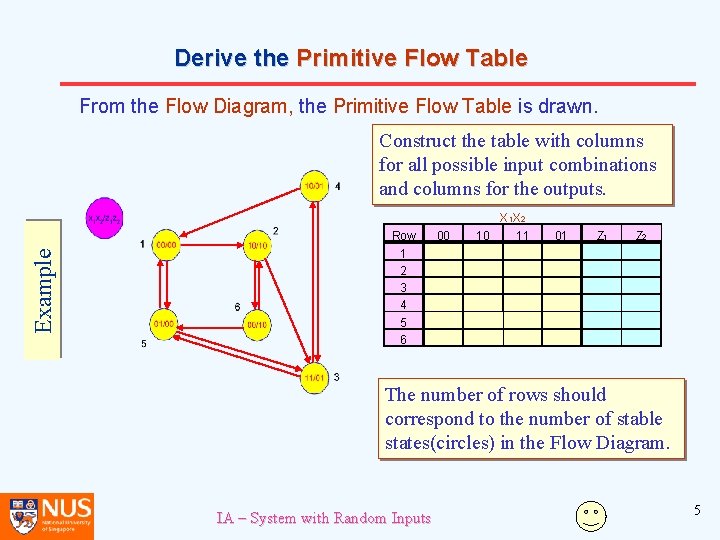
Derive the Primitive Flow Table From the Flow Diagram, the Primitive Flow Table is drawn. Construct the table with columns for all possible input combinations and columns for the outputs. Example Row 00 X 1 X 2 10 11 01 Z 2 1 2 3 4 5 6 The number of rows should correspond to the number of stable states(circles) in the Flow Diagram. IA – System with Random Inputs 5

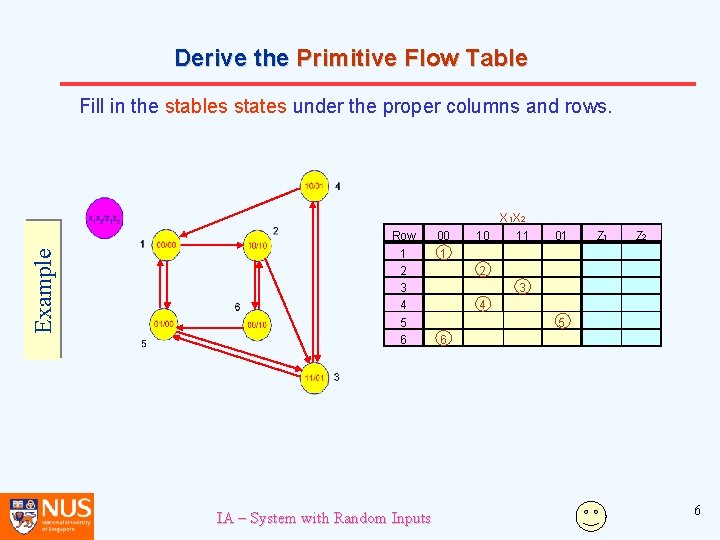
Derive the Primitive Flow Table Example Fill in the stables states under the proper columns and rows. Row 00 1 2 3 4 5 6 1 IA – System with Random Inputs X 1 X 2 10 11 01 Z 2 2 3 4 5 6 6

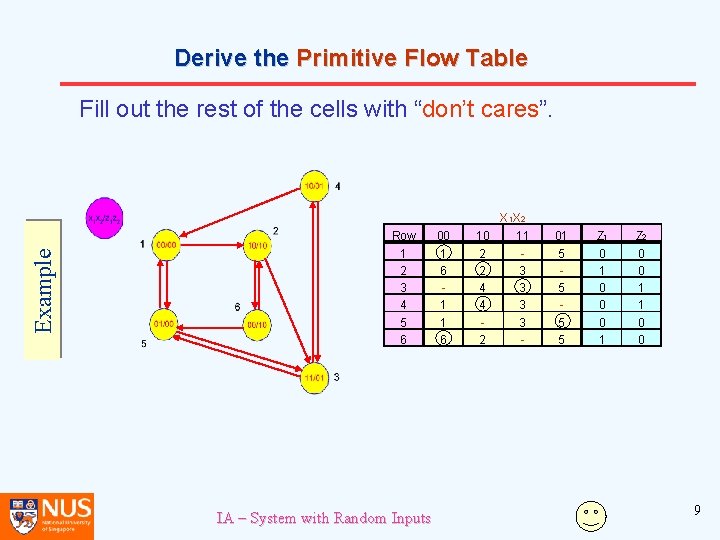
Derive the Primitive Flow Table Example Fill in the output states for every stable state. Row 00 1 2 3 4 5 6 1 IA – System with Random Inputs X 1 X 2 10 11 01 2 3 4 5 6 Z 1 Z 2 0 1 0 0 1 1 0 0 7

Derive the Primitive Flow Table Example Fill in the unstable states. Row 00 1 2 3 4 5 6 1 1 6 X 1 X 2 10 11 2 2 4 4 2 3 3 01 Z 2 5 0 1 0 0 1 1 0 0 5 5 5 You will need to refer to the Flow Diagram to determine the transitions between states. IA – System with Random Inputs 8

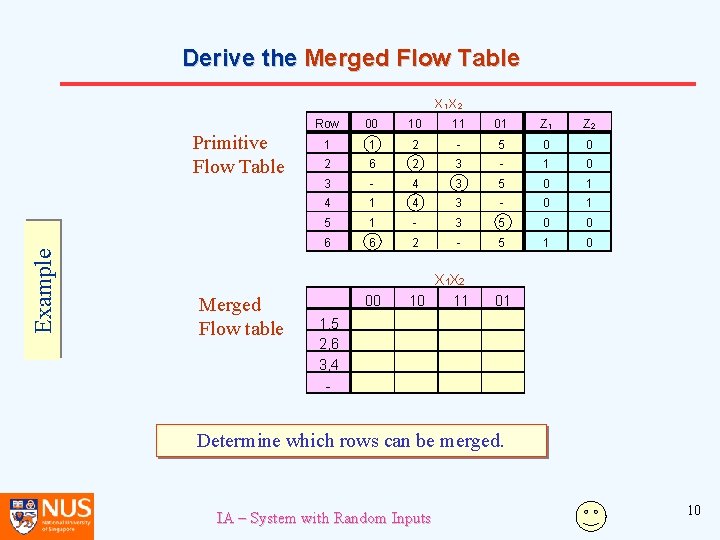
Derive the Primitive Flow Table Example Fill out the rest of the cells with “don’t cares”. Row 00 1 2 3 4 5 6 1 1 6 IA – System with Random Inputs X 1 X 2 10 11 2 2 4 4 2 3 3 - 01 Z 2 5 5 0 1 0 0 1 1 0 0 9

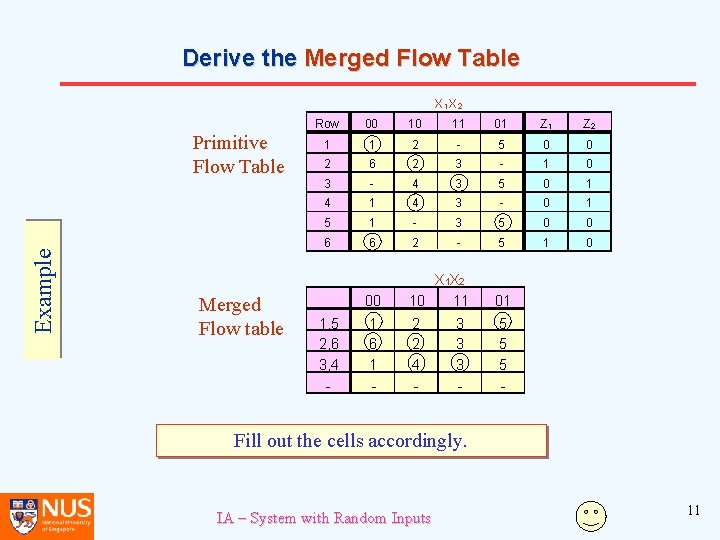
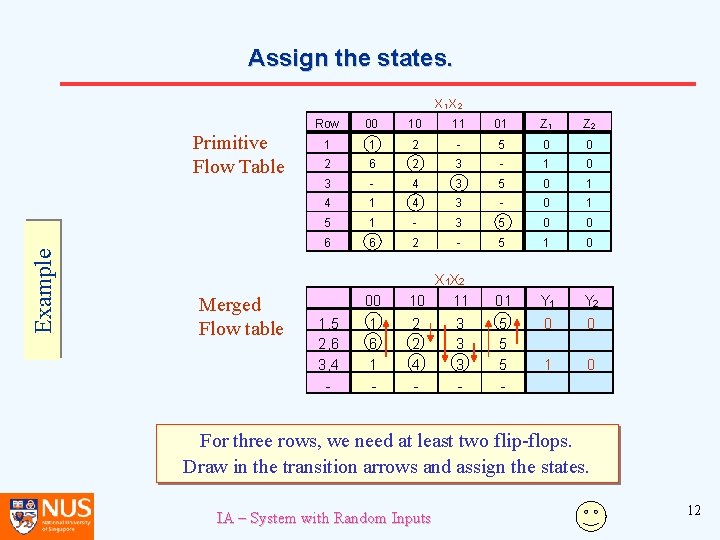
Derive the Merged Flow Table X 1 X 2 Example Primitive Flow Table Merged Flow table Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 00 X 1 X 2 10 11 01 1, 5 2, 6 3, 4 - Determine which rows can be merged. IA – System with Random Inputs 10

Derive the Merged Flow Table X 1 X 2 Example Primitive Flow Table Merged Flow table Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 - 00 X 1 X 2 10 11 01 1 6 1 - 2 2 4 - 5 5 5 - 3 3 3 - Fill out the cells accordingly. IA – System with Random Inputs 11

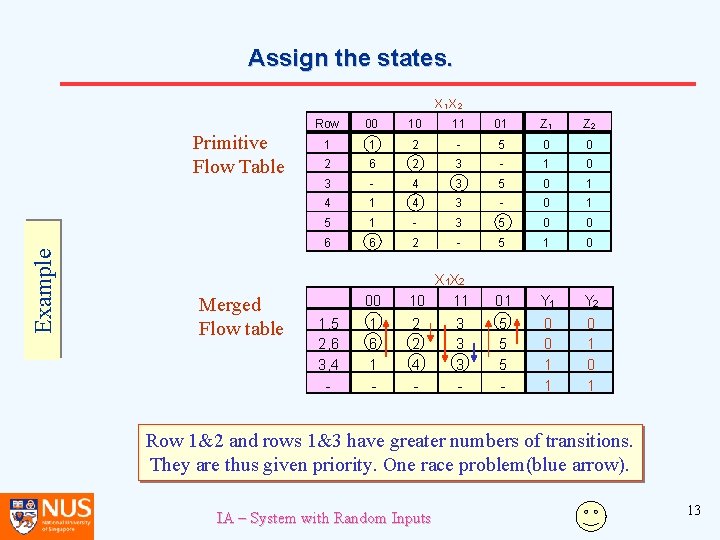
Assign the states. X 1 X 2 Example Primitive Flow Table Merged Flow table Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 00 X 1 X 2 10 11 01 Y 2 1 6 1 - 2 2 4 - 5 5 5 - 0 0 1, 5 2, 6 3, 4 - 3 3 3 - For three rows, we need at least two flip-flops. Draw in the transition arrows and assign the states. IA – System with Random Inputs 12

Assign the states. X 1 X 2 Example Primitive Flow Table Merged Flow table Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 00 X 1 X 2 10 11 01 Y 2 1 6 1 - 2 2 4 - 5 5 5 - 0 0 1 1, 5 2, 6 3, 4 - 3 3 3 - Row 1&2 and rows 1&3 have greater numbers of transitions. They are thus given priority. One race problem(blue arrow). IA – System with Random Inputs 13

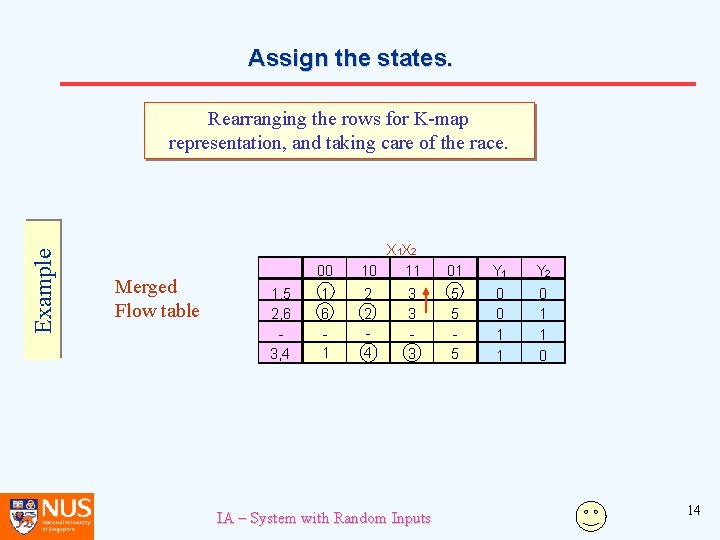
Assign the states. Example Rearranging the rows for K-map representation, and taking care of the race. Merged Flow table 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 IA – System with Random Inputs 14

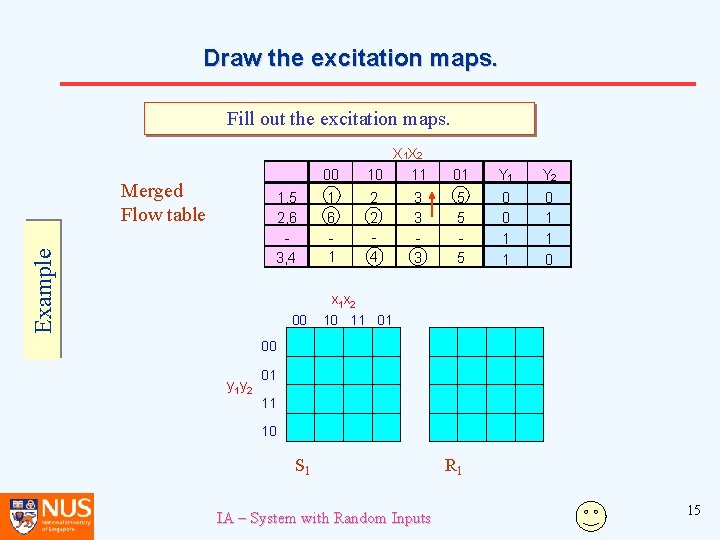
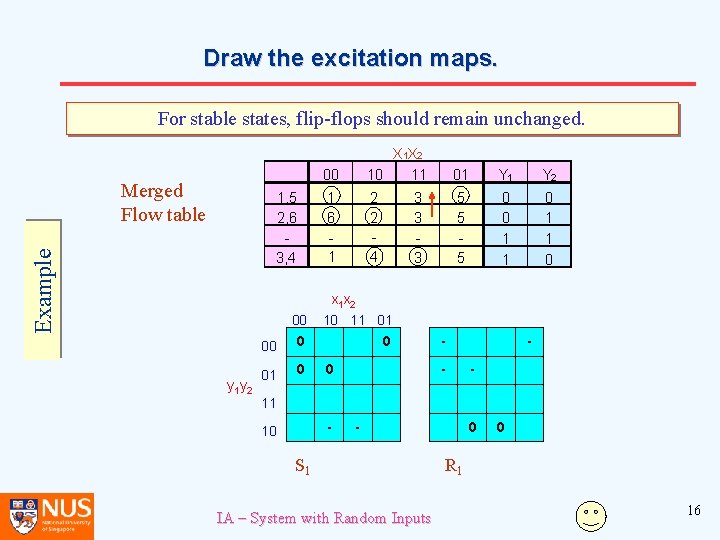
Draw the excitation maps. Fill out the excitation maps. Merged Flow table Example 1, 5 2, 6 3, 4 00 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 x 1 x 2 10 11 01 00 y 1 y 2 0 01 11 10 S 1 IA – System with Random Inputs R 1 15

Draw the excitation maps. For stable states, flip-flops should remain unchanged. Merged Flow table Example 1, 5 2, 6 3, 4 y 1 y 2 00 00 0 01 0 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 x 1 x 2 10 11 01 0 - - 11 - 10 - S 1 IA – System with Random Inputs 0 0 R 1 16

Draw the excitation maps. For unstable states, move to the respective stable states. Merged Flow table Example 1, 5 2, 6 3, 4 y 1 y 2 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 x 1 x 2 10 11 01 0 - - 00 00 0 01 0 0 - - 0 1 0 0 1 11 10 S 1 IA – System with Random Inputs R 1 17

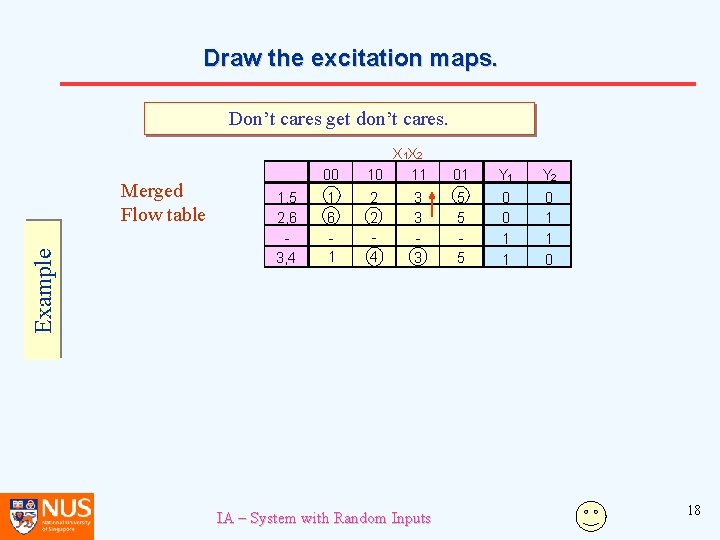
Draw the excitation maps. Don’t cares get don’t cares. Example Merged Flow table 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 IA – System with Random Inputs 18

Example Get the Boolean expressions for Set/Reset inputs. IA – System with Random Inputs 19

Example Set/Reset inputs for Y 2. IA – System with Random Inputs 20

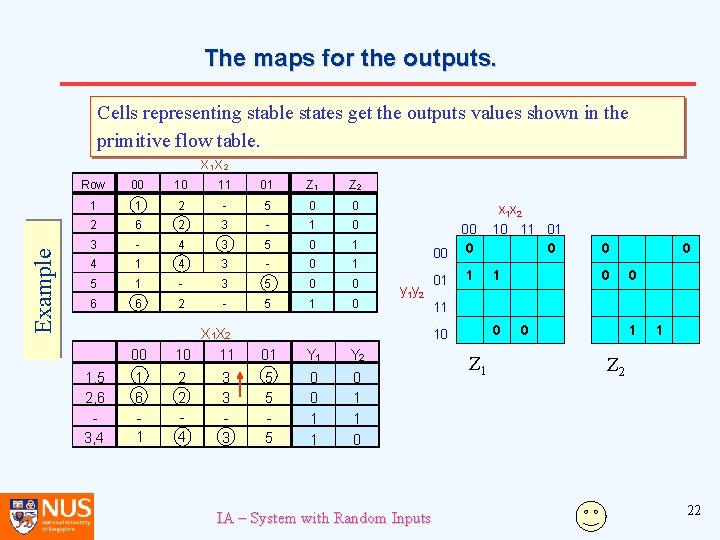
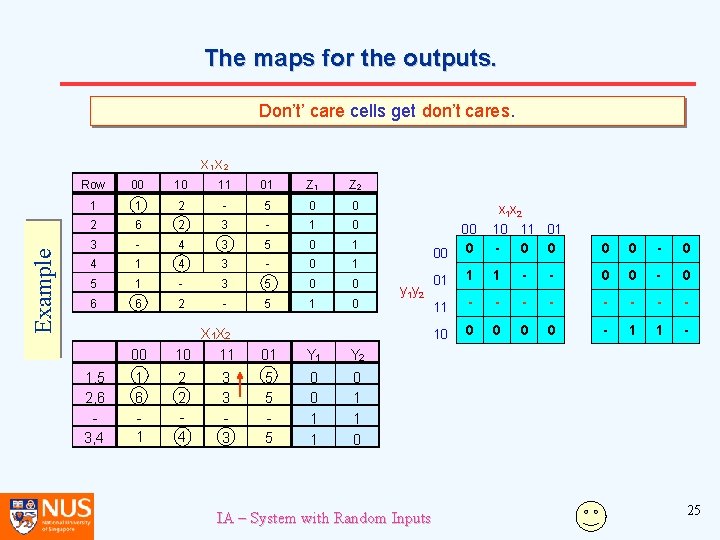
The maps for the outputs. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 00 x 1 x 2 10 11 01 00 y 1 y 2 01 11 10 IA – System with Random Inputs Z 1 Z 2 21

The maps for the outputs. Cells representing stable states get the outputs values shown in the primitive flow table. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 00 00 0 y 1 y 2 01 1 0 0 0 11 0 10 IA – System with Random Inputs x 1 x 2 10 11 01 0 Z 1 0 1 1 Z 2 22

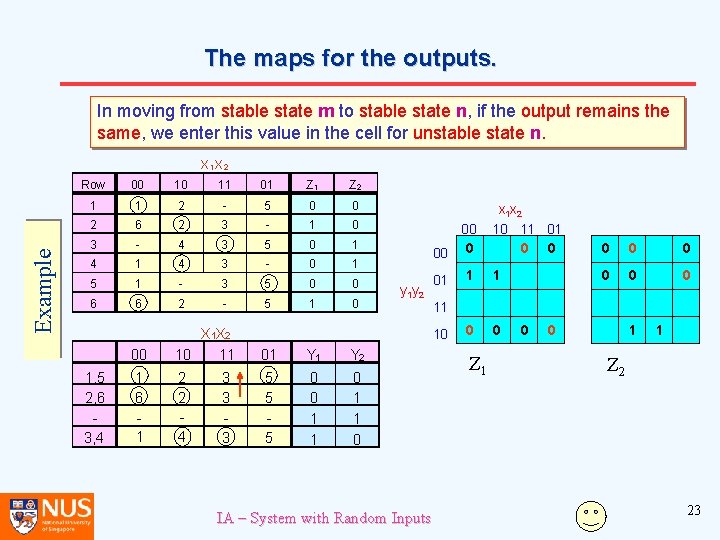
The maps for the outputs. In moving from stable state m to stable state n, if the output remains the same, we enter this value in the cell for unstable state n. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 x 1 x 2 10 11 01 0 0 0 1 1 0 0 00 00 0 y 1 y 2 01 11 10 IA – System with Random Inputs Z 1 0 0 1 1 Z 2 23

The maps for the outputs. In moving from stable state m to stable state n, if the output changes, we enter a “don’t care” in the cell for unstable state n. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 x 1 x 2 10 11 01 0 0 - 0 1 1 - - 0 0 0 0 0 - 1 1 - 00 00 0 y 1 y 2 01 11 10 IA – System with Random Inputs Z 1 Z 2 24

The maps for the outputs. Don’t’ care cells get don’t cares. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 00 00 0 y 1 y 2 IA – System with Random Inputs x 1 x 2 10 11 01 0 0 - 0 01 1 1 - - 0 0 - 0 11 - - - - 10 0 0 - 1 1 - 25

Derive the Boolean expressions for the outputs. Example X 1 X 2 Row 00 10 11 01 Z 2 1 1 2 - 5 0 0 2 6 2 3 - 1 0 3 - 4 3 5 0 1 4 3 - 0 1 5 1 - 3 5 0 0 6 6 2 - 5 1 0 1, 5 2, 6 3, 4 00 X 1 X 2 10 11 01 Y 2 1 6 1 2 2 4 5 5 5 0 0 1 1 0 3 3 3 00 00 0 y 1 y 2 IA – System with Random Inputs x 1 x 2 10 11 01 0 0 - 0 01 1 1 - - 0 0 - 0 11 - - - - 10 0 0 - 1 1 - 26

Review of the START Pushbutton The START pushbutton is required only for singlecycle fixed sequences which needs to be initiated. Example: START A+, B-, C+, C-, A- IA – System with Random Inputs 27

Review of the START Pushbutton For other cases, for example systems with random inputs, there is no need for a START pushbutton. Example: Alarm Annunciator System IA – System with Random Inputs 28

Incorporating the START Pushbutton Consider the example discussed earlier. . . Example START, A+, A- IA – System with Random Inputs 29

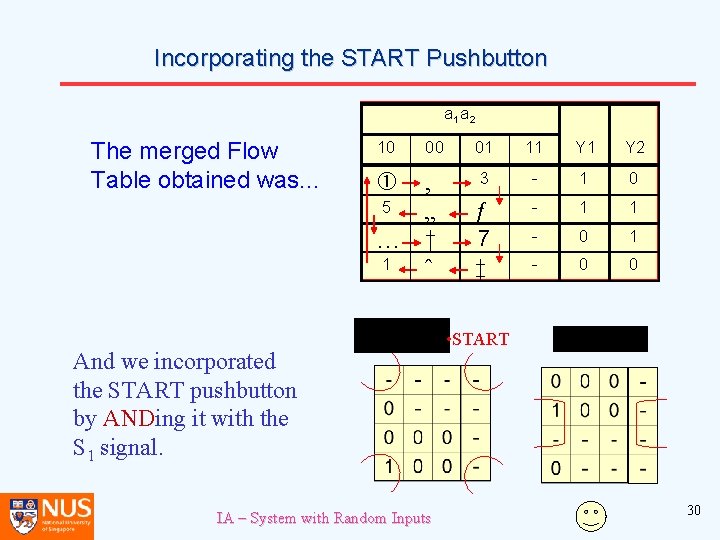
Incorporating the START Pushbutton a 1 a 2 The merged Flow Table obtained was. . . 10 00 ‚ 5 „ … † 1 ˆ And we incorporated the START pushbutton by ANDing it with the S 1 signal. IA – System with Random Inputs 01 11 Y 2 3 - 1 0 ƒ - 1 1 7 - 0 1 ‡ - 0 0 • START 30

Incorporating the START Pushbutton • But it is not always the case that the START pushbutton is ANDed with the S 1 signal. • The function of incorporating the START pushbutton is to force the sequence to stop at the end of the cycle. • In the example given, it is stopped in the Unstable 1 state. Pushing the START button will allow the system to jump to Stable State 1, thereby starting another sequence. IA – System with Random Inputs 31

Incorporating the START Pushbutton a 1 a 2 Example • If the states of the flip-flops were assigned as. . . Then START will need to be ANDed with the R 2 signal to stop the sequence in Unstable 1. Actuation of START will cause the system to jump to Stable 1. 10 00 ‚ 5 „ … † 1 ˆ 01 11 Y 2 3 - 0 0 ƒ - 1 0 7 - 1 1 ‡ - 0 1 • START 0 0 0 - - - 1 0 0 - - - - 0 0 0 - - - 1 IA – System with Random Inputs 0 0 32

Examples of Systems with Random Inputs IA – System with Random Inputs 33

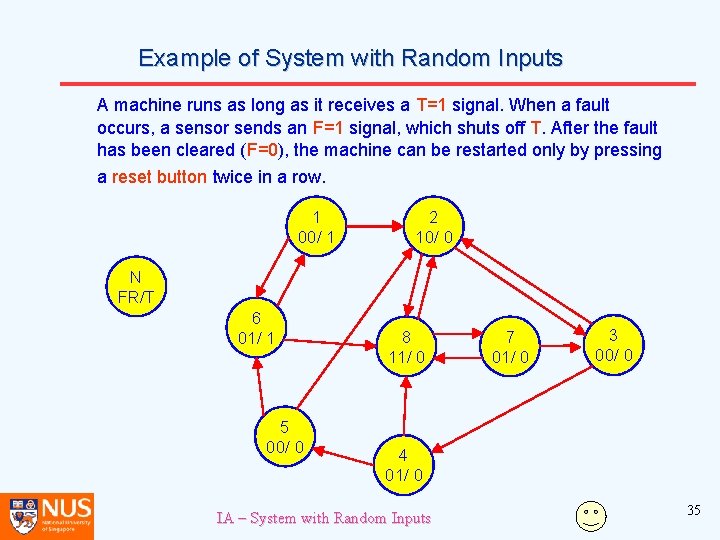
Example 1 Example of System with Random Inputs A machine runs as long as it receives a T=1 signal. When a fault occurs, a sensor sends an F=1 signal, which shuts off T. After the fault has been cleared (F=0), the machine can be restarted only by pressing a reset button twice in a row. This provision is intended to prevent a false restarting of the machine due to accidental touching of the reset button. Design a logic system to fulfill the above requirements. IA – System with Random Inputs 34

Example of System with Random Inputs A machine runs as long as it receives a T=1 signal. When a fault occurs, a sensor sends an F=1 signal, which shuts off T. After the fault has been cleared (F=0), the machine can be restarted only by pressing a reset button twice in a row. 1 00/ 1 2 10/ 0 N FR/T 6 01/ 1 5 00/ 0 8 11/ 0 7 01/ 0 3 00/ 0 4 01/ 0 IA – System with Random Inputs 35

Constructing the Primitive Flow Table FR Row 1 00 01 11 Construct the table and enter first the stable states and the outputs. ‚ 0 ƒ 0 „ 4 5 6 T 1 2 3 10 0 … † ‡ 7 8 IA – System with Random Inputs 0 1 - 0 ˆ 0 Primitive Flow Table 36

Constructing the Primitive Flow Table FR Row 1 For each stable state, determine which other stable states it moves to and fill in the unstable states. 00 2 3 3 ƒ 4 5 5 6 … 7 3 8 IA – System with Random Inputs 1 01 6 11 10 2 T 1 8 ‚ 0 4 „ 2 8 6 † ‡ 7 0 0 2 8 0 1 8 0 ˆ 2 0 Primitive Flow Table 37

Constructing the Primitive Flow Table FR Row 1 Fill in the don’t cares. 00 01 6 11 - 10 2 T 1 2 3 - 8 ‚ 0 3 ƒ 4 - 2 0 4 5 8 - 0 5 6 … 8 2 - 0 1 7 3 8 - 0 8 - 2 0 1 „ 6 † ‡ 7 ˆ Primitive Flow Table IA – System with Random Inputs 38

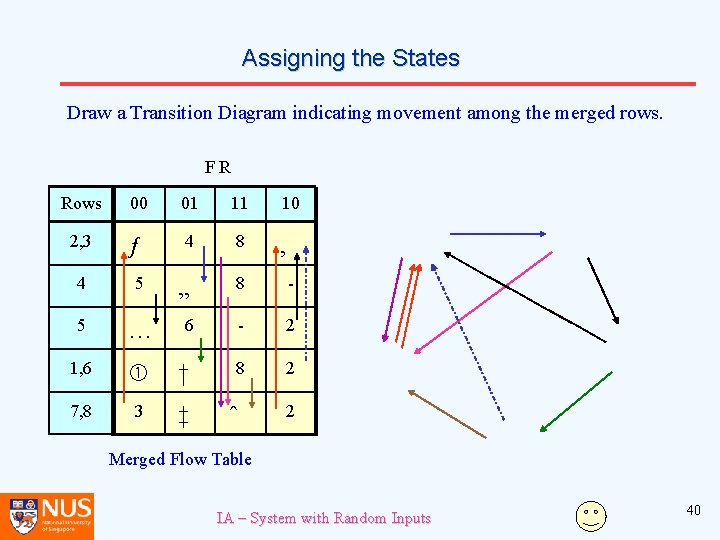
Constructing the Merged Flow Table FR F R Row 00 01 11 10 T 1 6 - 2 1 2 3 - 8 3 ƒ 4 - 2 0 4 5 8 - 0 5 … 6 - 2 0 6 1 8 - 1 7 3 † ‡ 8 - 0 8 - 7 2 0 „ ˆ ‚ Rows 0 Primitive Flow Table IA – System with Random Inputs 00 01 11 10 2, 3 ƒ 4 8 ‚ 4 5 „ 8 - 5 … 6 - 2 1, 6 † 8 2 7, 8 3 ‡ ˆ 2 Merged Flow Table 39

Assigning the States Draw a Transition Diagram indicating movement among the merged rows. FR Rows 00 01 11 10 2, 3 ƒ 4 8 ‚ 4 5 „ 8 - 5 … 6 - 2 1, 6 † 8 2 7, 8 3 ‡ ˆ 2 Merged Flow Table IA – System with Random Inputs 40

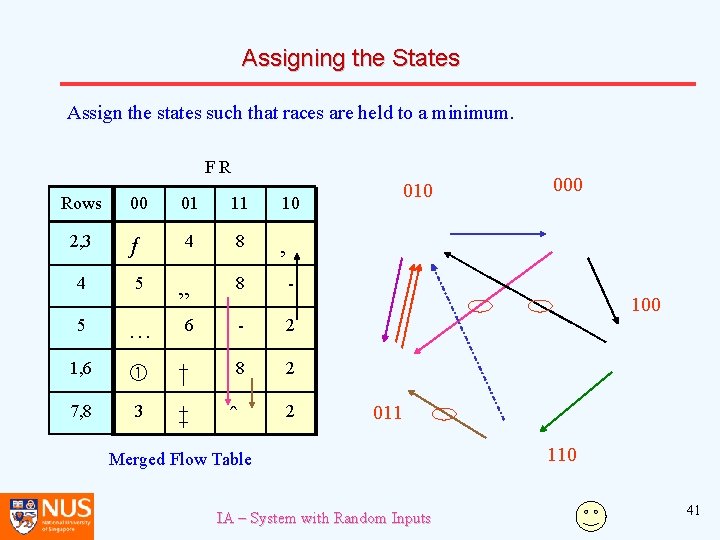
Assigning the States Assign the states such that races are held to a minimum. FR Rows 00 01 11 10 2, 3 ƒ 4 8 ‚ 4 5 „ 8 010 000 - 100 5 … 6 - 2 1, 6 † 8 2 7, 8 3 ‡ ˆ 2 011 Merged Flow Table IA – System with Random Inputs 110 41

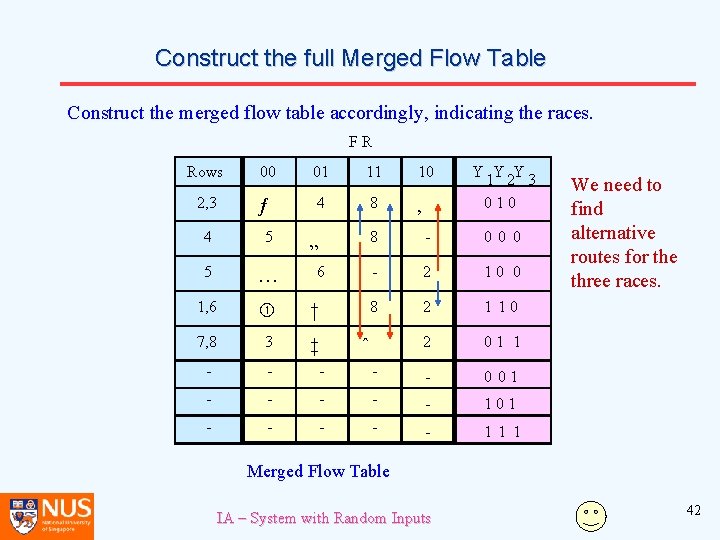
Construct the full Merged Flow Table Construct the merged flow table accordingly, indicating the races. FR Rows 2, 3 00 01 11 10 ƒ 4 8 ‚ 4 5 5 … 1, 6 † 7, 8 3 ‡ - - - - Y Y Y 1 2 3 010 8 - 0 0 0 - 2 10 0 8 2 1 10 2 01 1 - - 0 01 - - - 1 1 1 „ 6 ˆ We need to find alternative routes for the three races. Merged Flow Table IA – System with Random Inputs 42

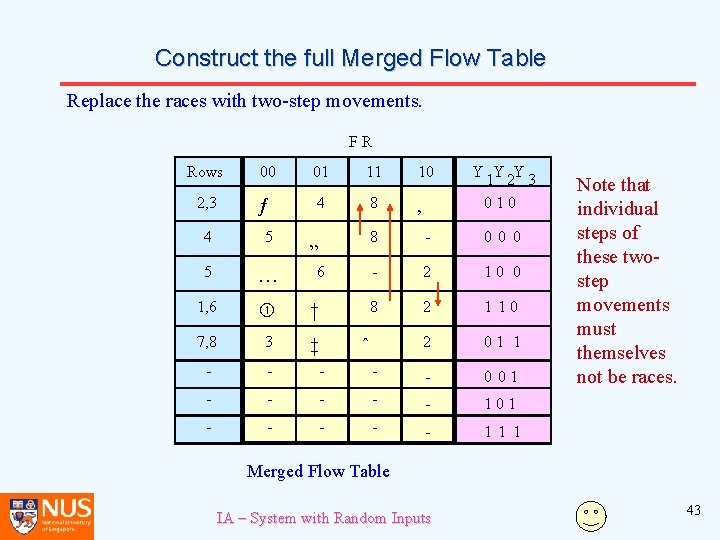
Construct the full Merged Flow Table Replace the races with two-step movements. FR Rows 2, 3 00 01 11 10 ƒ 4 8 ‚ 4 5 5 … 1, 6 † 7, 8 3 ‡ - - - - Y Y Y 1 2 3 010 8 - 0 0 0 - 2 10 0 8 2 1 10 2 01 1 - - 0 01 - - - 1 1 1 „ 6 ˆ Note that individual steps of these twostep movements must themselves not be races. Merged Flow Table IA – System with Random Inputs 43

Construct the K-map for the S and R inputs For cells with stable states… and the don’t cares. . . FR Rows 2, 3 00 01 11 10 ƒ 4 8 ‚ 4 5 5 … 1, 6 † 7, 8 3 ‡ - - - - Y Y Y 1 2 3 010 0 - 0 0 0 - 2 10 0 - 8 2 1 10 - 2 01 1 - - 0 01 - - - 6 ˆ 0 - 0 0 - - - - - 101 - - - 1 1 1 - - - S 1 - - 0 IA – System with Random Inputs - 0 Merged Flow Table - 0 8 „ 0 R 1 44

Construct the K-map for the S and R inputs For cells with unstable states… FR Rows 2, 3 00 01 11 10 ƒ 4 8 ‚ Y Y Y 1 2 3 010 0 0 - - 8 - 0 0 0 1 0 0 - - - - 2 10 0 - - 0 0 - 0 8 2 1 10 - - 0 0 1 1 2 01 1 0 0 - - - 0 01 - - - - - - 1 1 1 - - - - 4 5 5 … 1, 6 † 7, 8 3 ‡ - - - - „ 6 ˆ Merged Flow Table IA – System with Random Inputs S 1 R 1 45

And the others. . . Similarly the K-maps for the S and R inputs for the flip-flops Y 2 and Y 3 are derived. The K-map for the output T is then derived using both the merged flow table and the primitive flow table. IA – System with Random Inputs 46

Systems with Inputs which are not completely random X 1 Example 2 X 2 Parts with a rectangular cross-section move on a conveyor belt. As shown above, two photoelectric sensor, x 1 and x 2, detect whether a part passing through is “standing up” or “lying down”. The sensor output is a logic 1 if a part is detected. The parts are required to be in the sequence (DOWN, UP) with this sequence repeated continuously. Any incoming part which breaks this required sequence will cause an output signal T=1 is to be produced. This is used to actuate a cylinder which pushes these parts off the conveyor belt. IA – System with Random Inputs 47

Systems with Inputs which are not completely random Example 2 Note that the inputs X 1 and X 2 are not completely randomly actuated. As a “lying down” part and a “standing up” part passes through, they change as shown. When a “down” part passes through, X 1 X 2 go through 00, 01, 00. When an “up” part passes through, X 1 X 2 go through 00, 01, 10, 00. IA – System with Random Inputs 48

When a “down” part passes through, X 1 X 2 go through 00, 01, 00. When an “up” part passes through, X 1 X 2 go through 00, 01, 10, 00. 10 10/1 9 11/0 12 10/1 11 11/0 1 00/0 2 01/0 3 00/0 4 01/0 8 10/0 7 11/0 6 01/0 5 00/0 13 00/1 IA – System with Random Inputs 49

End of Random Inputs IA – System with Random Inputs 50