Sequential Projection Learning for Hashing with Compact Codes

Sequential Projection Learning for Hashing with Compact Codes 1 Jun Wang, 2 Sanjiv Kumar, and 1 Shih-Fu Chang 1 Columbia University, New York, USA 2 Google Research, New York, USA

Nearest Neighbor Search Nearest neighbor search in large databases with high dimensional points is important (e. g. image/video/document retrieval) � Exact search not practical � Ø Computational cost Ø Storage cost (need to store original data points) � Approximate nearest neighbor (ANN) Ø Tree approaches (KD tree, metric tree, ball tree, … ) Ø Hashing methods (locality sensitive hashing, spectral hashing, …)

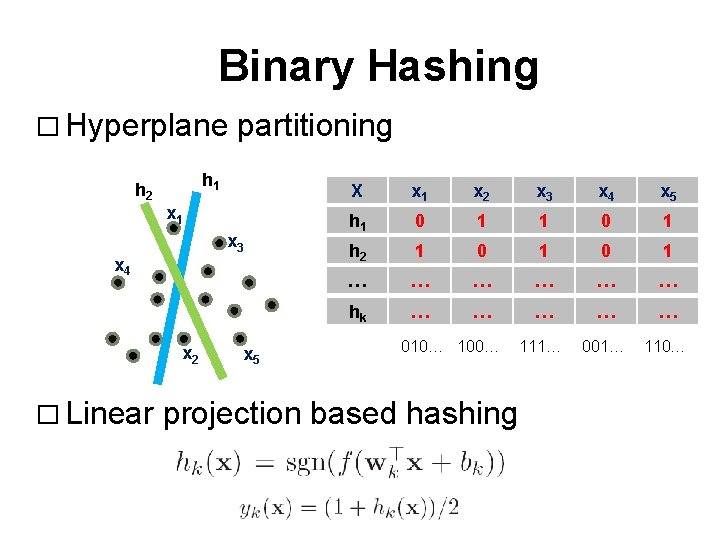
Binary Hashing � Hyperplane h 2 h 1 x 3 x 4 x 2 � Linear partitioning x 5 X x 1 x 2 x 3 x 4 x 5 h 1 0 1 h 2 1 0 1 … … … hk … … … 111… 001… 110… 010… 100… projection based hashing

Related Work � Different choices of projections Ø random projections ü locality sensitive hashing (LSH, Indyk et al. 98) ü shift invariant kernel hashing (SIKH, Raginsky et al. 09) Ø principal projections ü spectral hashing (SH, Weiss, et al. 08) � Different choices of Ø identity function: LSH & Boosted SSC (Shakhnarovich, 05) Ø sinusoidal function: SH & SIKH � Other recent work: Ø Restricted boltzman machines (RBMs, Hinton et al. 06) Ø Jian et al. 08 (metric learning) Ø Kulis et al. 09 & Mu et al. 10 (kernerlized) Ø Kulis NIPS 09 (binary reconstructive embedding)

Main Issues � Existing hashing methods mostly rely on random or principal projections Ø not compact Ø low accuracy � Simple metrics are usually not enough to express semantic similarity Ø Similarity given by a few pairwise labels � Goal: to learn binary hash functions that give high accuracy with compact codes --- semi-supervised and unsupervised cases

Formulation x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8

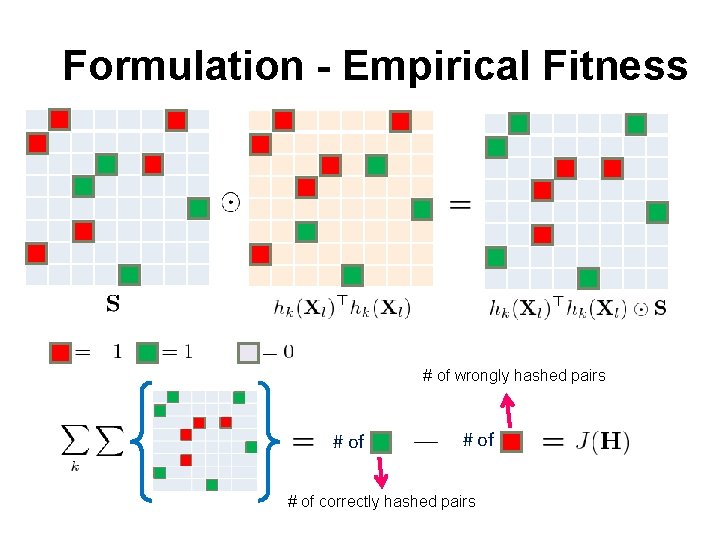
Formulation - Empirical Fitness # of wrongly hashed pairs # of correctly hashed pairs

Empirical Fitness � How well the hash codes fit on the training data � Recall the definition of pair-wise label metric � Objective:

Relaxing Empirical Fitness � Replace the sign of projections with the signed magnitude � A more simplified matrix form as:

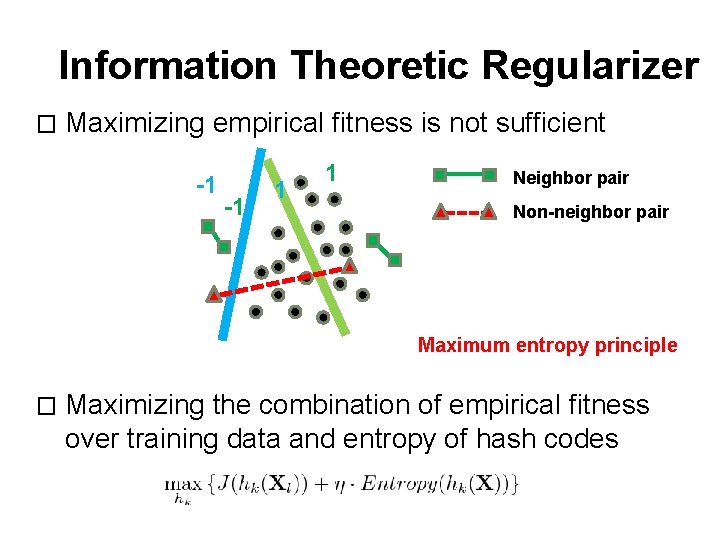
Information Theoretic Regularizer � Maximizing empirical fitness is not sufficient -1 -1 1 1 Neighbor pair Non-neighbor pair Maximum entropy principle � Maximizing the combination of empirical fitness over training data and entropy of hash codes

Relaxing Regularization Term � Step 1: Maximum entropy equals balanced partition � Step 2: Balanced partition equals partition with maximum variance � Step 3: Substitute the maximum bit-variance term by its lower bound

Final Objective “adjusted” covariance matrix � Orthogonal solution by Eigen-decomposition on adjusted covariance matrix M Not very accurate!

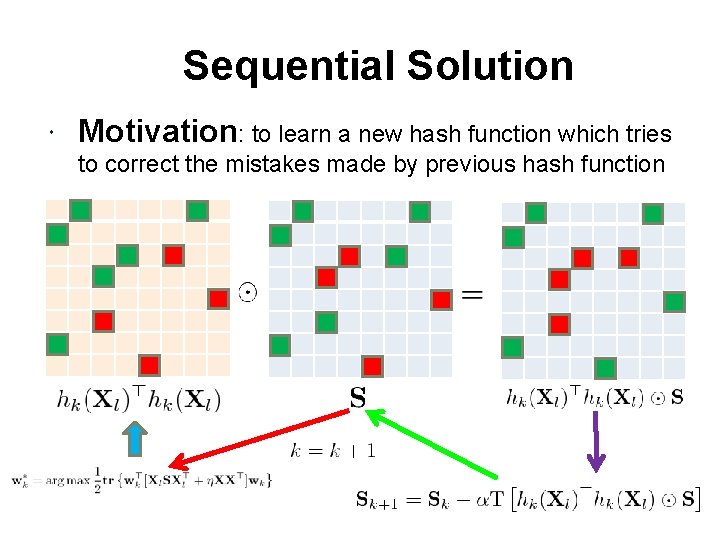
Sequential Solution Motivation: to learn a new hash function which tries to correct the mistakes made by previous hash function

S 3 PLH Algorithm Summary

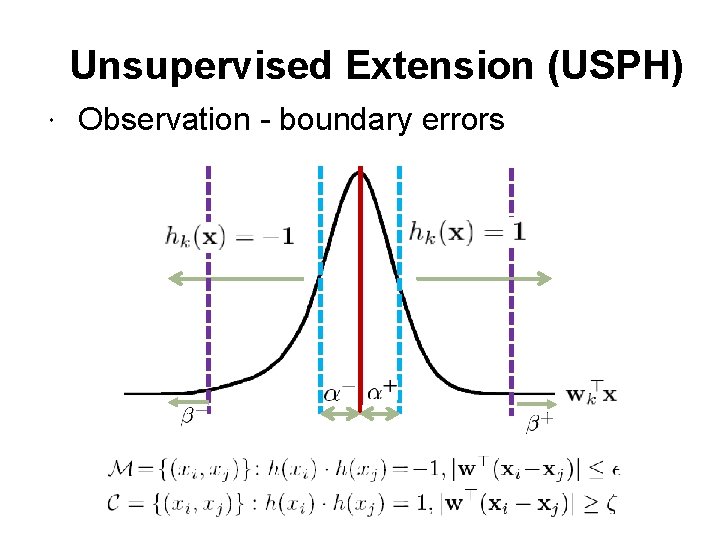
Unsupervised Extension (USPH) Observation - boundary errors

Pseudo Pair-Wise Labels Pseudo set of labeled data from contains all the point pairs: Accordingly, generate a pseudo label matrix Different with SPLH, USPLH generates new pseudo labels and the corresponding label matrix, instead of updating weights of a fixed set of given labels.

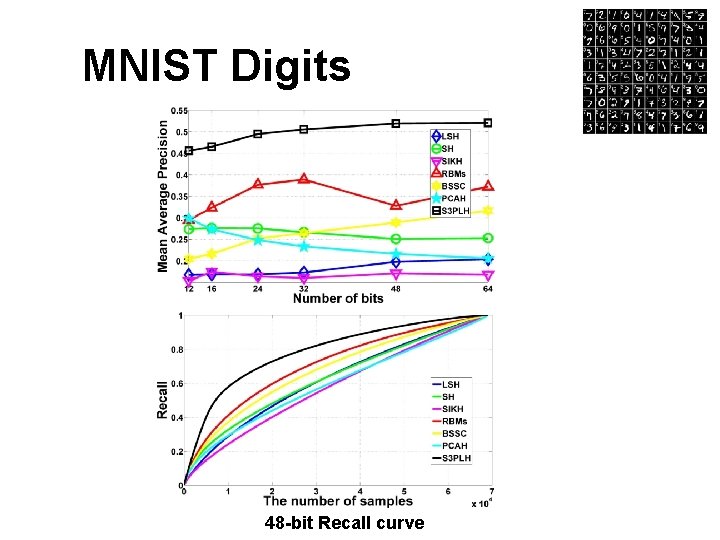
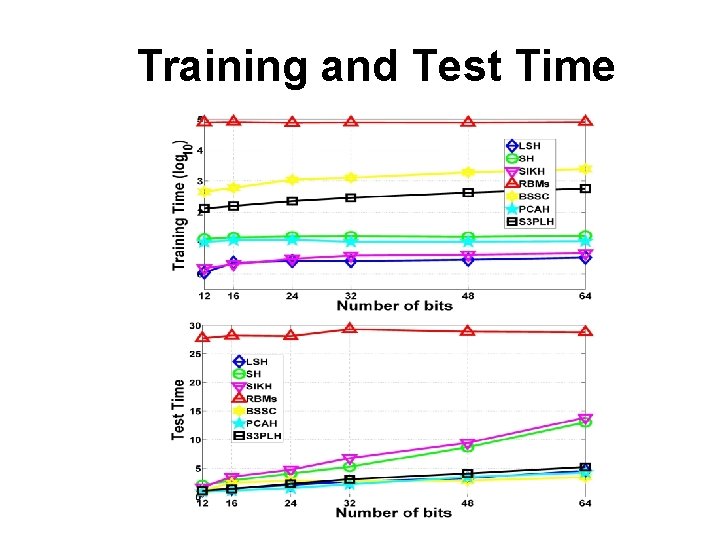
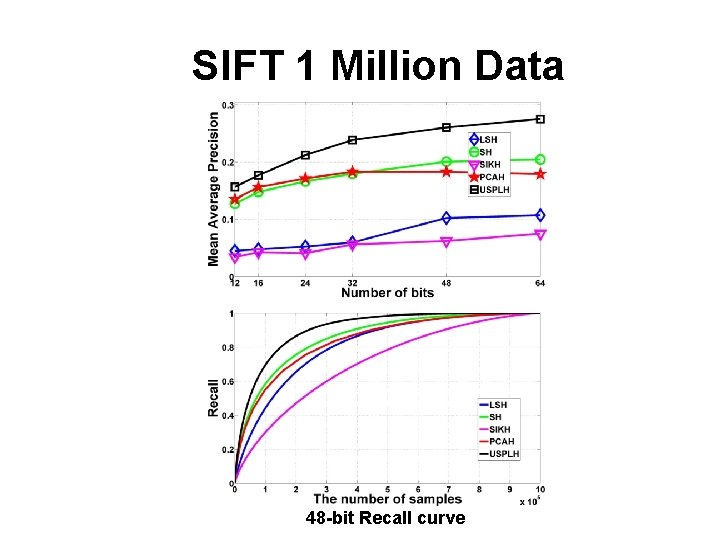
Experiments Datasets Ø MNIST (70 K) – supervised case Ø SIFT Data (1 Million SIFT features) – unsupervised case � Evaluation protocol Ø Mean Average Precision and Recall � Setting of training: MNIST data semi-supervised: 1 K labeled samples for training, 1 K for query test SIFT Data unsupervised: 2 K pseudo labels for training, 10 K for query test

MNIST Digits 48 -bit Recall curve

Training and Test Time

SIFT 1 Million Data 48 -bit Recall curve

Summary and Conclusion � Summary and contributions Ø A semi-supervised paradigm for hashing learning (Empirical risk with information theoretic regularization); Ø Sequential learning idea for error correction; Ø Extension of unsupervised case; Ø Easy implementation and highly scalable; � Future work Ø Theoretical analysis of performance guarantee Ø Weighted hamming embedding