Sequential Point Tree Carsten Dachsbacher Christian Vogelgsang Marc

Sequential Point Tree Carsten Dachsbacher Christian Vogelgsang Marc Stamminger Présentation : Thomas BARTHES Matthieu CORVAISIER

Plan • Rendu par points, objectifs et mise en œuvre • Point Trees – Sequential Point Trees – Point Tree Hierarchy • Approximations et erreurs • Du récursif au séquentiel – Rendu récursif – Séquentialisation – réarrangement • Extensions – Rendu hybride point/polygone – Couleurs et textures • Performances • Conclusion

Rendu par points • Avantages: – Très efficace pour le rendu d’objets complexes – Gestion facile et pratique du niveau de détails • Inconvénients: – Sélection des points effectuée par le CPU – La puissance du GPU n’est donc pas exploitée • Objectif: décharger un maximum de calculs depuis le CPU vers le GPU

Mise en œuvre • Obtenir une version séquentielle d’un arbre de points hiérarchique • Traitement de cette liste par le GPU: – Sélection du niveau de détails – Affichage de splats figurant les points

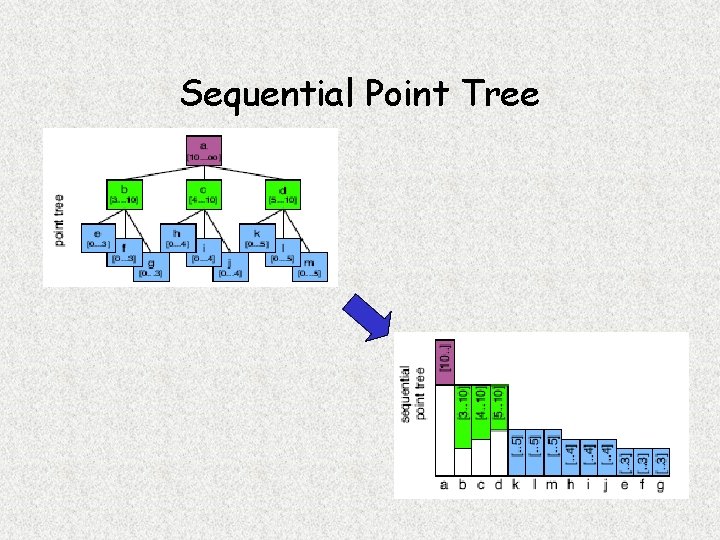
Sequential Point Tree

Point Tree Hierarchy • Construction d’un octree représentant la hiérarchie des points uniformément répartis sur l’objet • Calcul des moyennes des positions et des normales des points intermédiaires • Chaque nœud représente un morceau de l’objet • Un nœud équivaut à l’union de tous ses fils • Structure de données d’un nœud: – Point central p – Normale moyenne n – Diamètre de la sphère englobante d

Approximation d’un nœud par un disque • Chaque nœud de l’arbre peut être approximé par un disque – Même point central – Même normale – Même diamètre • L’erreur d’approximation est décrite par deux valeurs – Erreur perpendiculaire e. P – Erreur tangentielle e. T

Erreur perpendiculaire (1) • e. P = distance minimum entre 2 plans parallèles au disque qui englobent tous les disques fils

Erreur perpendiculaire (2) • Espace image: projection d’une erreur image ëP • ëP = e. P * sin(v, n) / |v| • ëP: varie en fonction de sinus(v, n) – v: vecteur du point de vue – n: vecteur normal du disque • ëP rend compte du fait que les erreurs le long des silhouettes sont moins acceptables (discontinuités) • Plus le point de vue est éloigné, plus ëP est faible

Erreur tangentielle (1) • e. T = diamètre du disque père – largeur minimale de l’ensemble des disques fils • Mesure si un disque parent couvre une trop grande surface • Conséquences: erreurs sur les bords des surfaces

Erreur tangentielle (2) • Espace image: projection d’une erreur image ëT • ëT = e. T * cos(v, n) / |v| • ëT: varie en fonction de cosinus(v, n) – v: vecteur du point de vue – n: vecteur normal du disque • ëT rend compte du fait que les erreurs dans les plans faisant face au point de vue sont moins acceptables (trous) • Plus le point de vue est éloigné, plus ëT est faible

Erreur géométrique • Simplification: combinaison des erreurs perpendiculaire et tangentielle en une seule erreur géométrique • e. G = √(e. P² + e. T²) • Espace image: projection d’une erreur image ëG • ëG = e. G / |v| • ëG ne dépend plus de l’angle du point de vue

Rendu Récursif (1) • Un objet est affiché par un parcours en profondeur de la hiérarchie de points • Pour chaque nœud, l’erreur image ë est calculée • Si ë dépasse un seuil acceptable ε, et si le nœud n’est pas une feuille fils parcourus récursivement • Cas contraire affichage d’un splat de taille d/r (diamètre du nœud projeté dans l’espace image) • ε défini par l’utilisateur

Rendu Récursif (2) • Densité des points adaptée : – À la distance du point de vue: r – Aux propriétés locales de la surface

Séquentialisation (1) • Problème : procédure récursive non adaptée pour un traitement séquentiel rapide par le GPU • Solution : – réarranger l’arbre de données en une liste – remplacer la procédure de rendu récursif par une boucle séquentielle parcourant cette liste • Arrangement optimisé : toutes les entrées sélectionnées dans la liste sont regroupées dans un même segment

Séquentialisation (2) • CPU: – Mémorise dans chaque nœud les valeurs rmin et rmax – Stocke les nœuds dans une liste non hiérarchique – Trie la liste en fonction des rmax • GPU: – Test non récursif: r Є [rmin, rmax] – Affichage

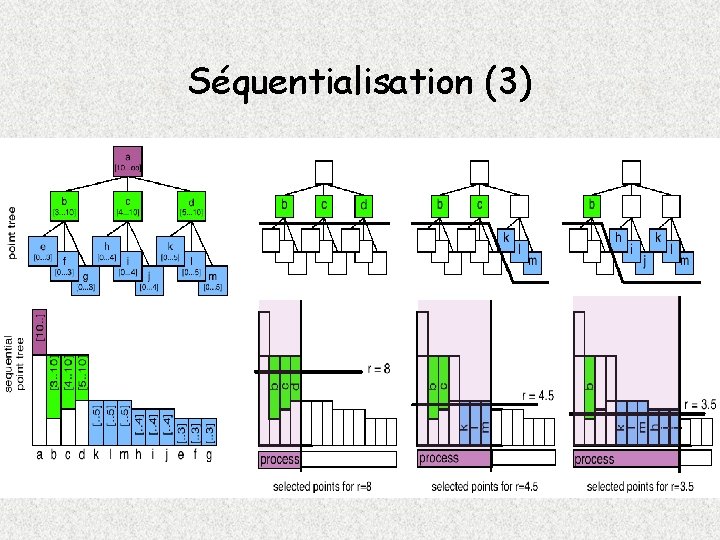
Séquentialisation (3)

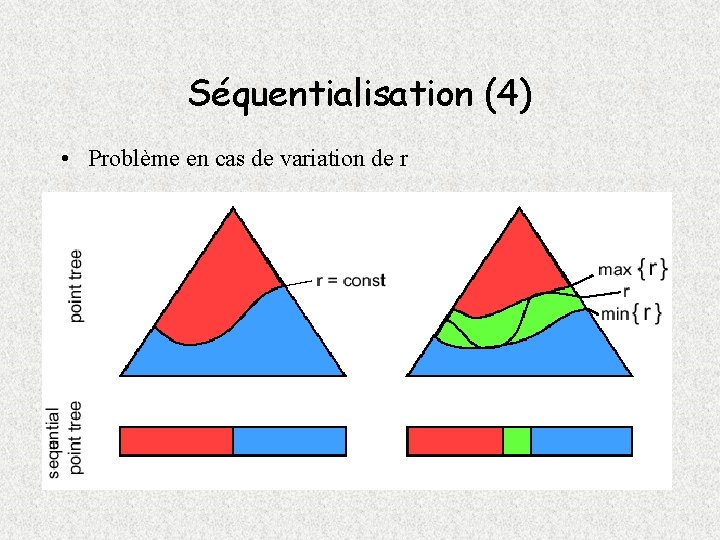
Séquentialisation (4) • Problème en cas de variation de r

Réarrangement • Le segment de liste exhaustif est envoyé au GPU • Le GPU effectue le test d’appartenance à [rmin, rmax] • Test vérifié : point rendu par un splat de diamètre d/r • Test non vérifié : point occulté (placé à l’infini) • Pourcentage de points occultés : 10 à 40 % (dépend de la variation de r)

Rendu Hybride • Extension possible des sequential point trees : – Parties de l’objet rendues par des points – Parties de l’objet rendues par des polygones • But : sélection des polygones par le GPU

Couleur et Texture (1) • Possibilité de mémoriser la couleur dans un nœud • Couleur d’un nœud interne = moyenne de celle de ses fils • Problème avec les grands splats : contours flous • Obligation de reconsidérer l’erreur géométrique • Solution : augmenter l’erreur de chaque point pour forcer l’affichage de petits splats

Couleur et Texture (2)

Performances (1) • Matériel et logiciel : ATI Radeon 9700 avec Direct. X • Affichage : – Statues et arbres : sequential point trees – Sol, ciel et autres modèles : polygones (triangles) • 77 millions de points envoyés par seconde au GPU, qui en affiche 50 millions après culling • Textures et données géométriques sont stockées dans la mémoire de la carte graphique

Performances (2) • Frame rates de l’ordre de 36 à 90 fps, avec une charge CPU de 5 à 15% sur un Pentium 2. 4 GHz • Essais avec nouvelle NVIDIA NV 30 résultats préliminaires, affichage possible de 80 millions de points par seconde après sélection par le GPU • Modèles avec lumière dynamique – Illumination locale calculée dans le vertex shader – 60 millions de splats affichés par seconde après culling du GPU – vertex shader exécuté 85 millions de fois par seconde

Conclusion • Sequential point trees version séquentielle des point trees hiérarchiques • Sélection du niveau de détails gérée quasi entièrement par le GPU, avec un simple vertex program • Affichage effectif de 50 millions de points par secondes sur un GPU actuel, faible charge CPU (idéal pour jeux vidéos…) • Extension proposée pour rendu hybride point/polygone, sans apparition d’artefacts

(Et pour finir) MAGNETO, SERGE… (La page web pour télécharger l’article et la vidéo) http: //www 9. informatik. uni-erlangen. de/Persons/Stamminger/Research/spt

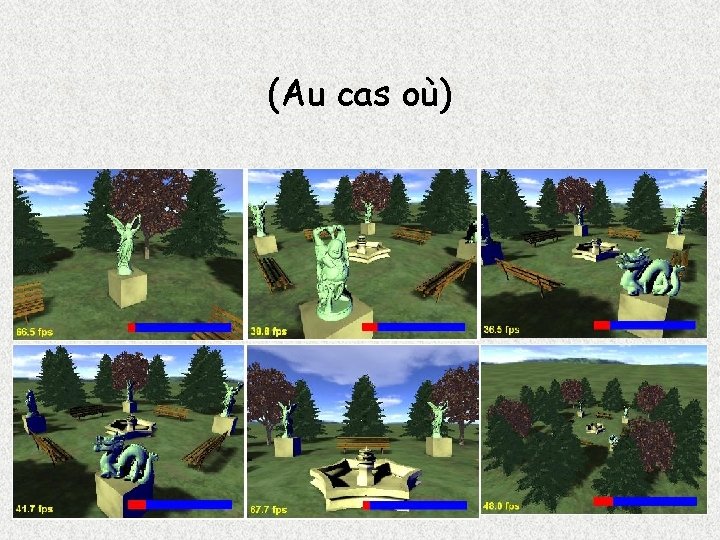
(Au cas où)