Sequential Logic Implementation z Models for representing sequential

Sequential Logic Implementation z Models for representing sequential circuits y Finite-state machines (Moore and Mealy) y Representation of memory (states) y Changes in state (transitions) z Design procedure y State diagrams y State transition table y Next state functions CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 1

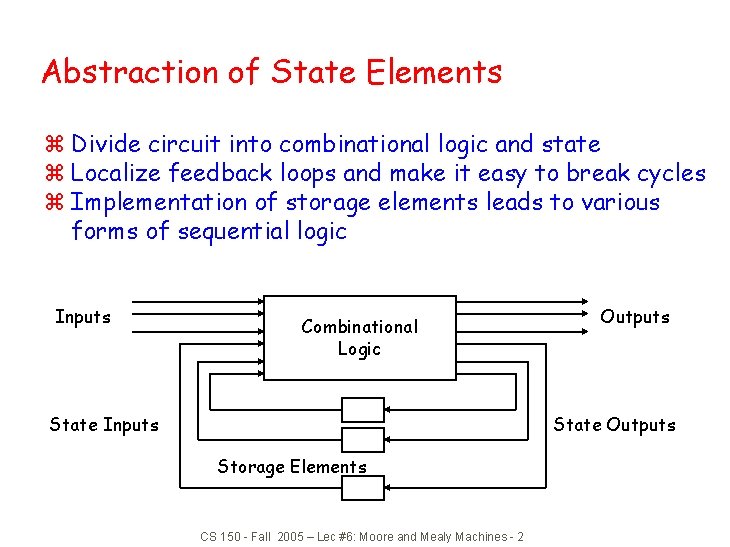
Abstraction of State Elements z Divide circuit into combinational logic and state z Localize feedback loops and make it easy to break cycles z Implementation of storage elements leads to various forms of sequential logic Inputs Combinational Logic State Inputs Outputs State Outputs Storage Elements CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 2

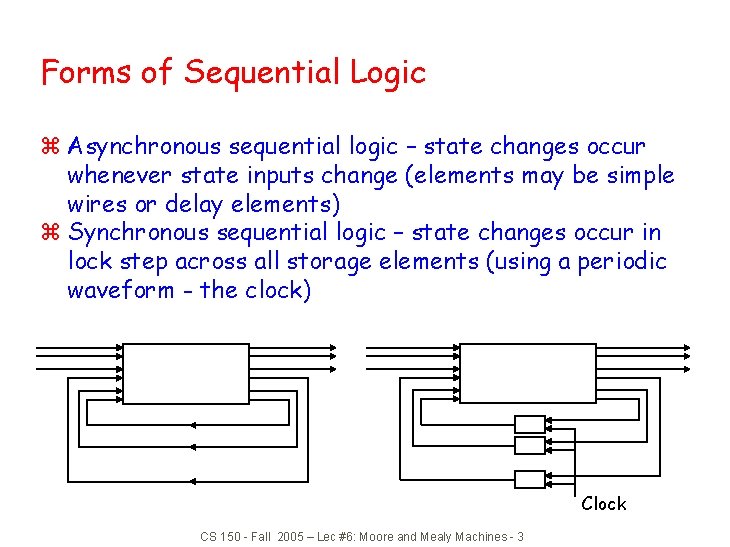
Forms of Sequential Logic z Asynchronous sequential logic – state changes occur whenever state inputs change (elements may be simple wires or delay elements) z Synchronous sequential logic – state changes occur in lock step across all storage elements (using a periodic waveform - the clock) Clock CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 3

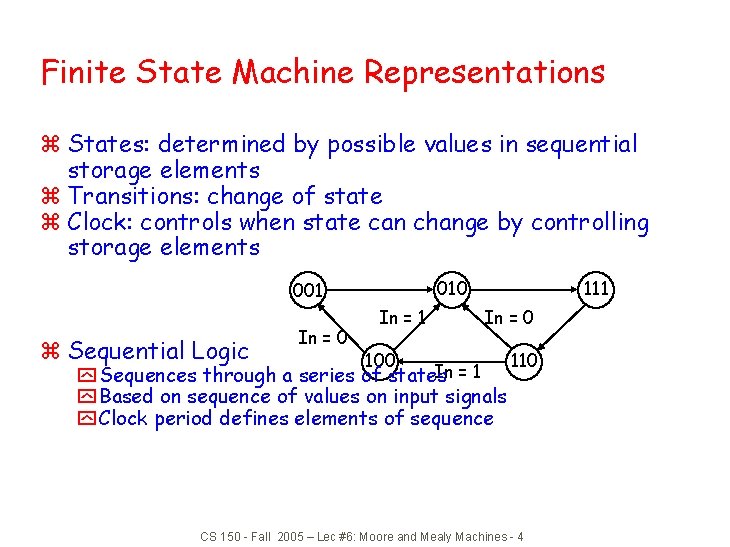
Finite State Machine Representations z States: determined by possible values in sequential storage elements z Transitions: change of state z Clock: controls when state can change by controlling storage elements 010 001 z Sequential Logic In = 0 In = 1 111 In = 0 100 In = 1 y Sequences through a series of states 110 y Based on sequence of values on input signals y Clock period defines elements of sequence CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 4

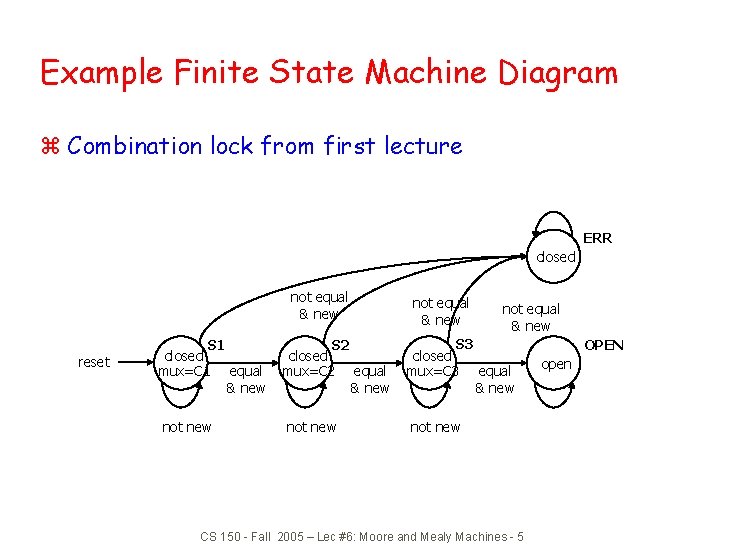
Example Finite State Machine Diagram z Combination lock from first lecture ERR closed not equal & new reset S 1 closed mux=C 1 equal & new not new S 2 closed mux=C 2 equal & new not equal & new S 3 closed mux=C 3 equal & new not new CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 5 OPEN open

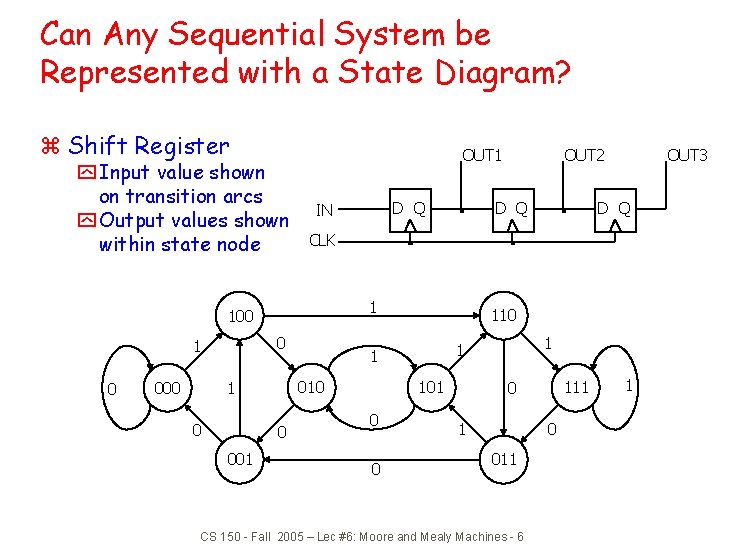
Can Any Sequential System be Represented with a State Diagram? z Shift Register y Input value shown on transition arcs y Output values shown within state node OUT 1 0 0 0 001 D Q 110 101 0 0 1 1 1 010 1 000 D Q OUT 3 CLK 100 1 D Q IN OUT 2 111 0 011 CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 6 1

Counters are Simple Finite State Machines z Counters y Proceed thru well-defined state sequence in response to enable z Many types of counters: binary, BCD, Gray-code y 3 -bit up-counter: 000, 001, 010, 011, 100, 101, 110, 111, 000, . . . y 3 -bit down-counter: 111, 110, 101, 100, 011, 010, 001, 000, 111, . . . 001 000 011 100 3 -bit up-counter 111 110 101 CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 7

Verilog Upcounter module binary_cntr inputs clk; outputs [2: 0] reg [2: 0] (q, clk) q; q; p; always @(q) //Calculate next state case (q) 3’b 000: p = 3’b 001; 3’b 001: p = 3’b 010; … 3’b 111: p = 3’b 000; endcase always @(posedge clk) q <= p; //next becomes current state endmodule CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 8

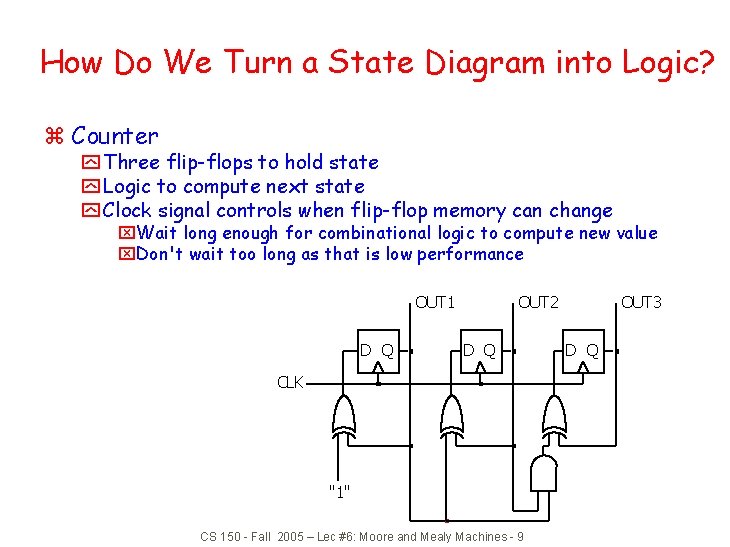
How Do We Turn a State Diagram into Logic? z Counter y Three flip-flops to hold state y Logic to compute next state y Clock signal controls when flip-flop memory can change x. Wait long enough for combinational logic to compute new value x. Don't wait too long as that is low performance OUT 1 D Q OUT 2 D Q CLK "1" CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 9 OUT 3 D Q

FSM Design Procedure z Start with counters y Simple because output is just state y Simple because no choice of next state based on input z State diagram to state transition table y Tabular form of state diagram y Like a truth-table z State encoding y Decide on representation of states y For counters it is simple: just its value z Implementation y Flip-flop for each state bit y Combinational logic based on encoding CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 10

FSM Design Procedure: State Diagram to Encoded State Transition Table z Tabular form of state diagram z Like a truth-table (specify output for all input combinations) z Encoding of states: easy for counters – just use value 001 000 011 100 3 -bit up-counter 111 110 101 current state 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 11 next state 001 1 010 2 011 3 100 4 101 5 110 6 111 7 000 0

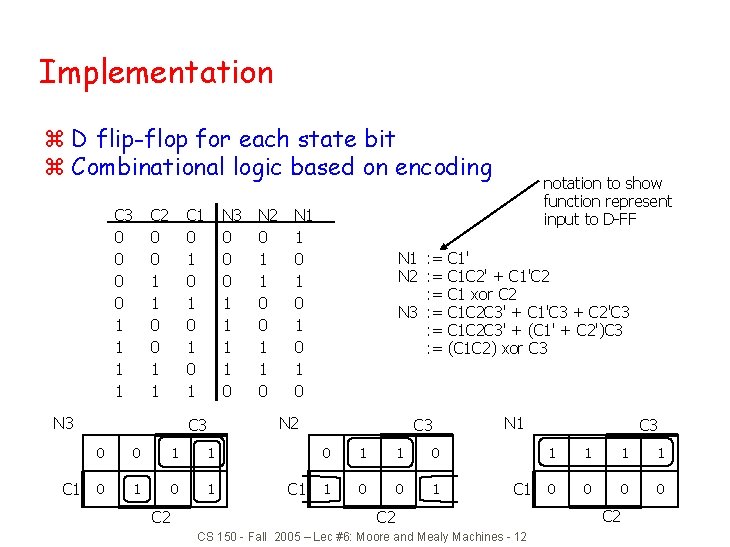
Implementation z D flip-flop for each state bit z Combinational logic based on encoding C 3 0 0 1 1 C 2 0 0 1 1 C 1 0 1 0 1 N 3 C 1 N 3 0 0 0 1 1 0 C 3 0 0 1 1 0 1 C 2 N 2 0 1 1 0 N 1 1 0 1 0 N 1 : = C 1' N 2 : = C 1 C 2' + C 1'C 2 : = C 1 xor C 2 N 3 : = C 1 C 2 C 3' + C 1'C 3 + C 2'C 3 : = C 1 C 2 C 3' + (C 1' + C 2')C 3 : = (C 1 C 2) xor C 3 N 2 C 1 notation to show function represent input to D-FF C 3 0 1 1 0 0 1 N 1 C 2 CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 12 C 3 1 1 0 0 C 2

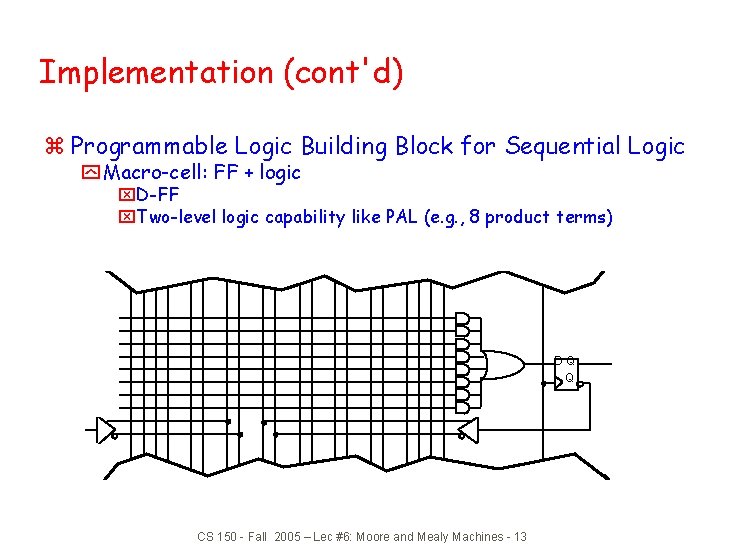
Implementation (cont'd) z Programmable Logic Building Block for Sequential Logic y Macro-cell: FF + logic x. D-FF x. Two-level logic capability like PAL (e. g. , 8 product terms) DQ Q CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 13

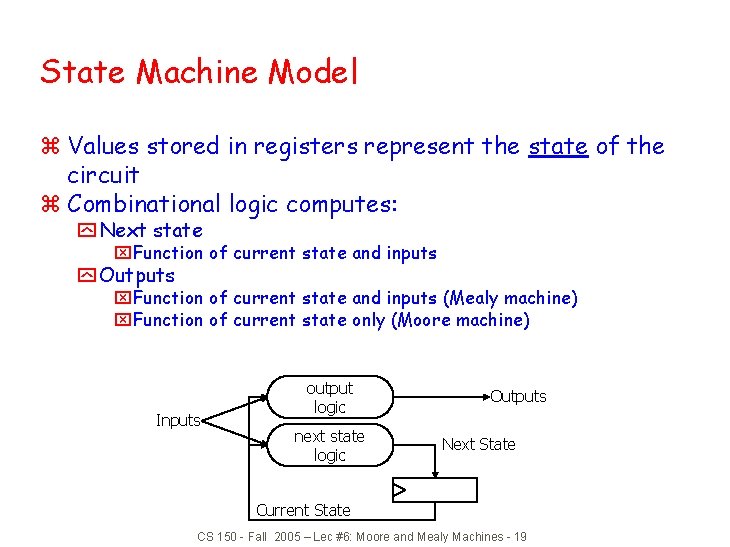
State Machine Model z Values stored in registers represent the state of the circuit z Combinational logic computes: y Next state x. Function of current state and inputs y Outputs x. Function of current state and inputs (Mealy machine) x. Function of current state only (Moore machine) Inputs output logic next state logic Outputs Next State Current State CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 19

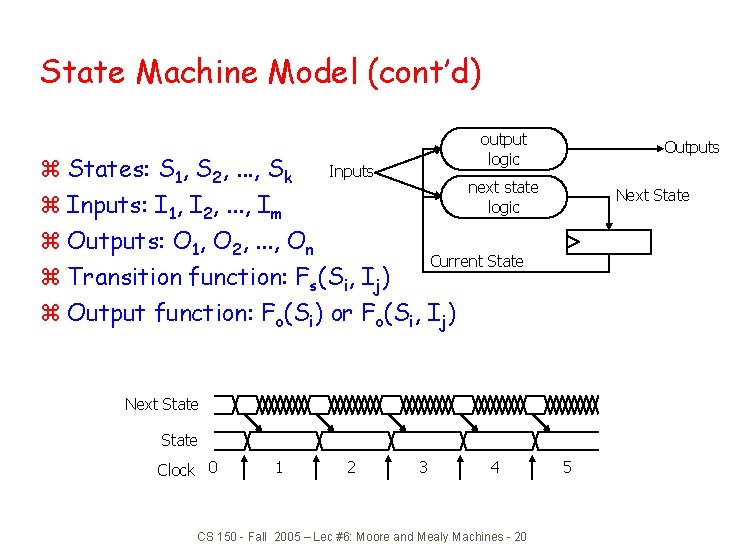
State Machine Model (cont’d) output logic Outputs z States: S 1, S 2, . . . , Sk Inputs next state logic z Inputs: I 1, I 2, . . . , Im z Outputs: O 1, O 2, . . . , On Current State z Transition function: Fs(Si, Ij) z Output function: Fo(Si) or Fo(Si, Ij) Next State Clock 0 1 2 3 4 CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 20 5

First Midterm Exam— 28 September 2005 z Topics to be covered: y Combinational logic design x From spec to truth table to K-map to Boolean Expression • Canonical forms of Boolean Expressions • Conversions of AND-OR logic to NAND or NOR logic x Two level logic implementations using gates, PLA, MUX, DEC, ROM, Xilinx CLB FPGA structures • Comparing implementation complexities/figures of merit • Combinational Verilog (lab expertise!) y Basic Sequential logic design x Flip flop behavior, analysis, and timing diagrams x Using flip flops to design registers, shifters, counters x From spec to state diagram to Sequential Verilog x Amount of FSM implementation through end of today CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 21

First Midterm Exam— 28 September 2005 z Exam mechanics y y Worth ONLY 10% of course grade In class, designed for 1 hour, full 80 minutes available WILL TAKE PLACE IN 125 CORY LABORATORY!!! No Blue Book—all work to be done on the exam paper! x Bring pencil and eraser—DUMB to use pen! x Cheating = 0 on exam—DO NOT DO IT! F in class plus letter to file for second offense y Closed Book, Closed Notes BUT x 8. 5” x 11” two-sided crib sheet OK • Developing your crib sheet is a great way to study • Don’t forget old exams and solutions are all on-line x No calculators, PDAs, laptops, camera phones, icq to experts … y Write assumptions if problem spec is ambiguous x Difficult to ask questions during the exam itself y Written regrade appeals policy CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 22

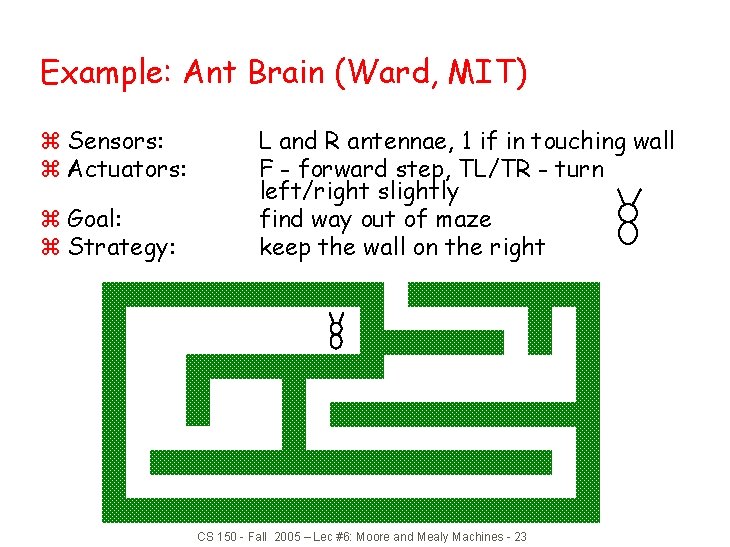
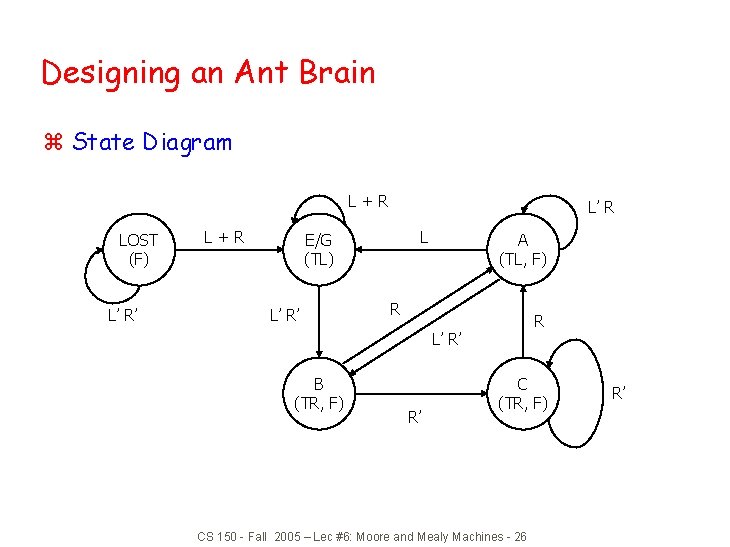
Example: Ant Brain (Ward, MIT) z Sensors: z Actuators: z Goal: z Strategy: L and R antennae, 1 if in touching wall F - forward step, TL/TR - turn left/right slightly find way out of maze keep the wall on the right CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 23

Ant Brain CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 24

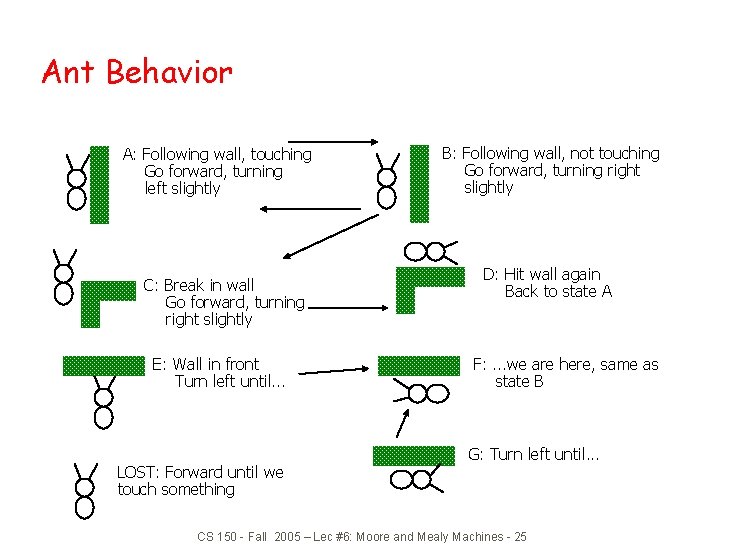
Ant Behavior A: Following wall, touching Go forward, turning left slightly C: Break in wall Go forward, turning right slightly E: Wall in front Turn left until. . . LOST: Forward until we touch something B: Following wall, not touching Go forward, turning right slightly D: Hit wall again Back to state A F: . . . we are here, same as state B G: Turn left until. . . CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 25

Designing an Ant Brain z State Diagram L+R LOST (F) L’ R’ L+R L’ R L E/G (TL) L’ R’ A (TL, F) R R L’ R’ B (TR, F) R’ C (TR, F) CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 26 R’

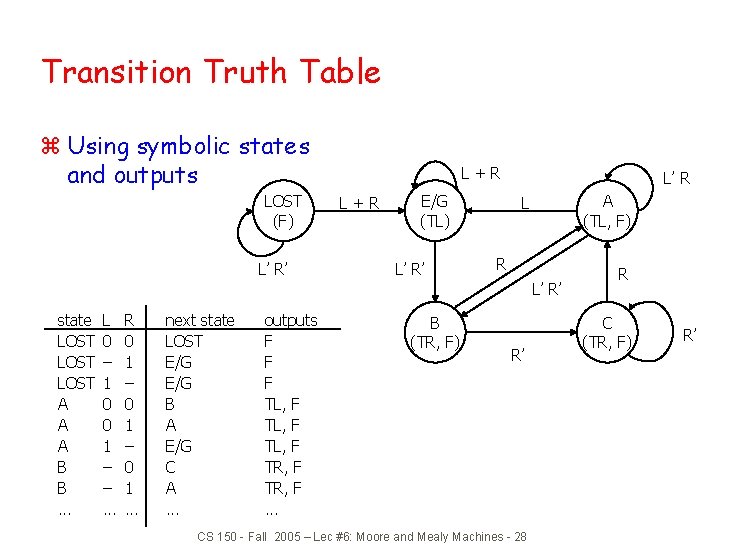
Synthesizing the Ant Brain Circuit z Encode States Using a Set of State Variables y Arbitrary choice - may affect cost, speed z Use Transition Truth Table y Define next state function for each state variable y Define output function for each output z Implement next state and output functions using combinational logic y 2 -level logic (ROM/PLA/PAL) y Multi-level logic y Next state and output functions can be optimized together CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 27

Transition Truth Table z Using symbolic states and outputs LOST (F) L’ R’ L+R E/G (TL) L’ R’ L’ R A (TL, F) L R L’ R’ state LOST A A A B B. . . L 0 – 1 0 0 1 – –. . . R 0 1 – 0 1. . . next state LOST E/G B A E/G C A. . . outputs F F F TL, F TR, F. . . B (TR, F) R’ CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 28 R C (TR, F) R’

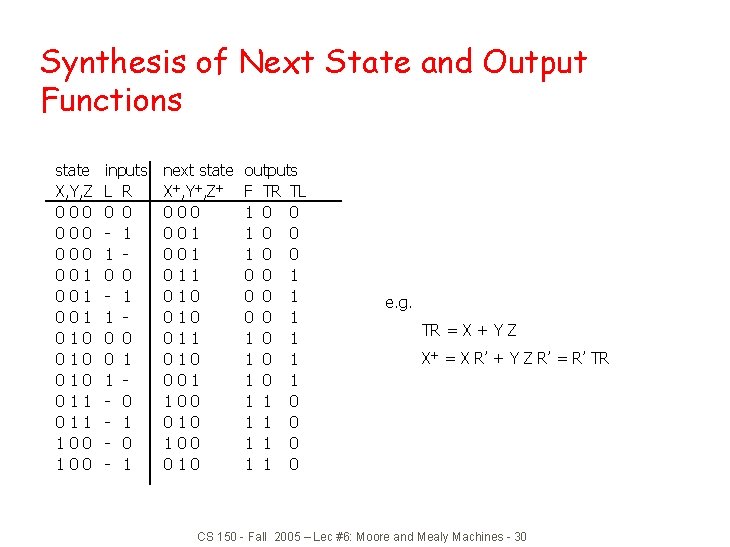
Synthesis z 5 states : at least 3 state variables required (X, Y, Z) y State assignment (in this case, arbitrarily chosen) state X, Y, Z 000. . . 010 010 011. . . L R 0 0 0 1. . . 0 0 0 1 1 0 0 0 1. . . next state X', Y', Z' 000 001. . . 011 010 001 100 010. . . outputs F TR TL 1 0 0. . . 1 0 1 1 1 0. . . it now remains to synthesize these 6 functions CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 29 LOST E/G A B C - 000 001 010 011 100

Synthesis of Next State and Output Functions state X, Y, Z 000 000 001 001 010 010 011 100 inputs L R 0 0 - 1 1 0 0 0 1 1 - 0 - 1 next state X+, Y+, Z+ 000 001 011 010 001 100 010 outputs F TR TL 1 0 0 1 0 0 1 1 0 1 1 0 e. g. TR = X + Y Z X+ = X R’ + Y Z R’ = R’ TR CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 30

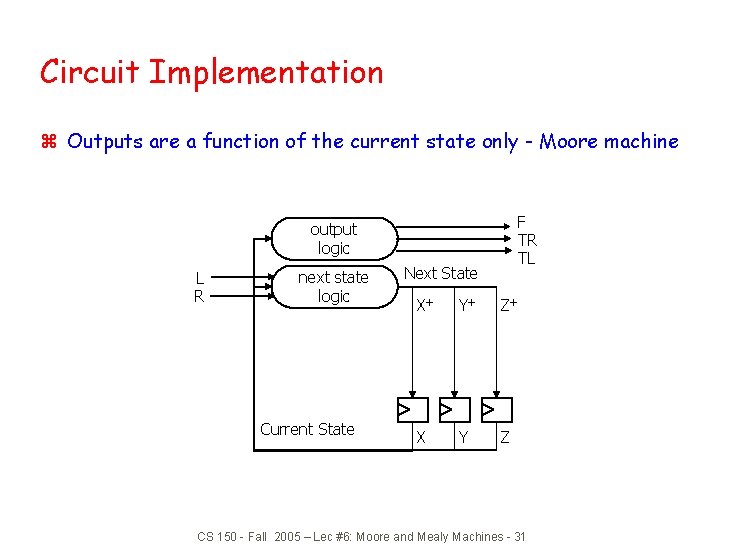
Circuit Implementation z Outputs are a function of the current state only - Moore machine F TR TL output logic L R next state logic Current State Next State X+ Y+ Z+ X Y Z CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 31

Verilog Sketch module ant_brain (F, TR, TL, L, R) inputs L, R; outputs F, TR, TL; reg X, Y, Z; assign F = function(X, Y, Z, L, R); assign TR = function(X, Y, Z, L, R); assign TL = function(X, Y, Z, L, R); always @(posedge clk) begin X <= function (X, Y, Z, L, R); Y <= function (X, Y, Z, L, R); Z <= function (X, Y, Z, L, R); endmodule CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 32

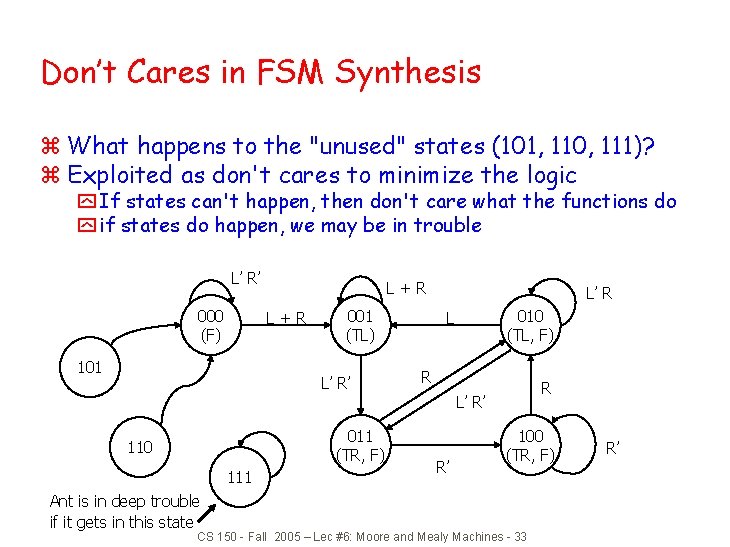
Don’t Cares in FSM Synthesis z What happens to the "unused" states (101, 110, 111)? z Exploited as don't cares to minimize the logic y If states can't happen, then don't care what the functions do y if states do happen, we may be in trouble L’ R’ 000 (F) L+R 101 001 (TL) L’ R’ L’ R 010 (TL, F) L R R L’ R’ 011 (TR, F) 110 111 Ant is in deep trouble if it gets in this state R’ 100 (TR, F) CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 33 R’

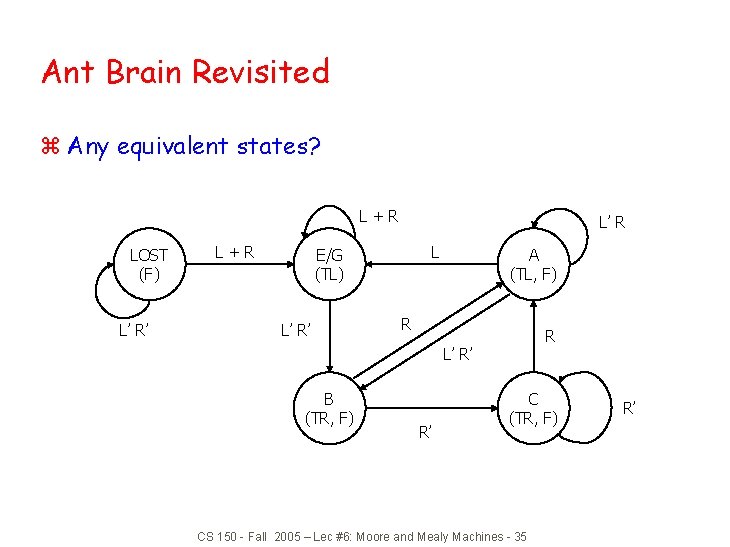
State Minimization z Fewer states may mean fewer state variables z High-level synthesis may generate many redundant states z Two state are equivalent if they are impossible to distinguish from the outputs of the FSM, i. e. , for any input sequence the outputs are the same z Two conditions for two states to be equivalent: y 1) Output must be the same in both states y 2) Must transition to equivalent states for all input combinations CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 34

Ant Brain Revisited z Any equivalent states? L+R LOST (F) L’ R’ L+R L’ R L E/G (TL) L’ R’ A (TL, F) R R L’ R’ B (TR, F) R’ C (TR, F) CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 35 R’

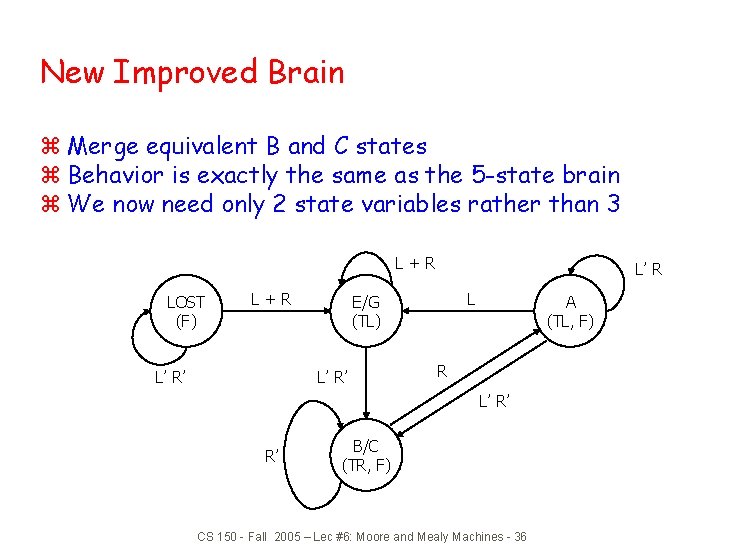
New Improved Brain z Merge equivalent B and C states z Behavior is exactly the same as the 5 -state brain z We now need only 2 state variables rather than 3 L+R LOST (F) L+R L’ R’ L’ R L E/G (TL) L’ R’ A (TL, F) R L’ R’ R’ B/C (TR, F) CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 36

New Brain Implementation state X, Y 00 00 00 01 01 01 10 10 10 11 11 inputs L R 0 0 - 1 1 0 0 0 1 1 - 0 - 1 next state outputs X', Y' F TR TL 00 1 0 0 01 1 0 0 1 01 0 0 1 11 1 0 1 10 1 01 1 0 1 11 1 1 0 10 1 1 0 X+ L X 0 0 1 0 0 0 1 1 Y+ 1 1 0 0 R L X 0 1 1 0 0 0 Y F L X 1 1 0 0 1 1 Y 1 1 1 0 0 1 1 R Y TR R L X 0 0 0 0 1 1 Y CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 37 0 0 TL R L X 0 0 1 1 0 0 Y 1 1 R

Sequential Logic Implementation Summary z Models for representing sequential circuits y Abstraction of sequential elements y Finite state machines and their state diagrams y Inputs/outputs y Mealy, Moore, and synchronous Mealy machines z Finite state machine design procedure y Deriving state diagram y Deriving state transition table y Determining next state and output functions y Implementing combinational logic CS 150 - Fall 2005 – Lec #6: Moore and Mealy Machines - 38