Sequencing algorithms for multiple machines Operations scheduling Nahmias

Sequencing algorithms for multiple machines Operations scheduling, Nahmias

Sequencing Algorithms for multiple machines • Assume that n jobs are to be processed through m machines. • The number of possible schedule is staggering, even for moderate values of both n and m. • For each machine there are n! different ordering of the jobs. – If the jobs may be processed on the machines in any order, it follows that there are (n!)m possible schedules. – For example, for n=5 and m=5, there are 24, 833 x 1010 , possible schedules.

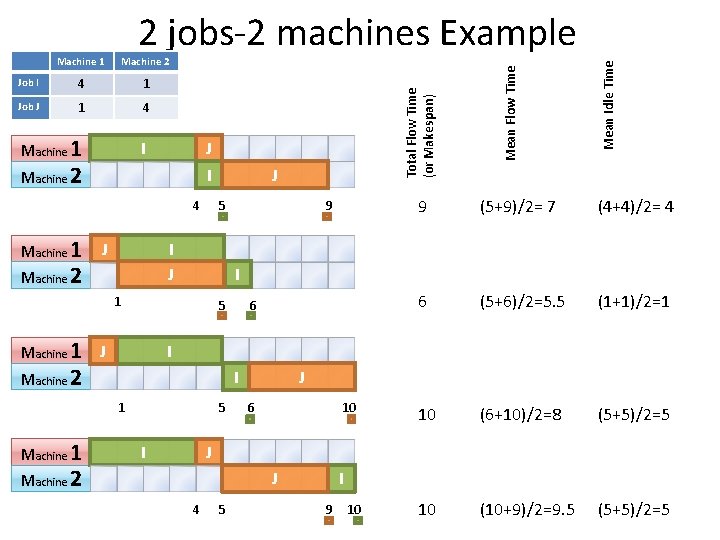
Job I 4 1 Job J 1 4 Machine 1 Machine 2 I J I 4 Machine 1 Machine 2 J 5 I J 5 9 (5+9)/2= 7 (4+4)/2= 4 6 6 (5+6)/2=5. 5 (1+1)/2=1 10 (6+10)/2=8 (5+5)/2=5 10 (10+9)/2=9. 5 (5+5)/2=5 I J I 1 Machine 2 9 I 1 Machine 2 J Mean Idle Time Machine 2 Mean Flow Time Machine 1 Total Flow Time (or Makespan) 2 jobs-2 machines Example 5 I J 6 10 J J 4 5 I 9 10

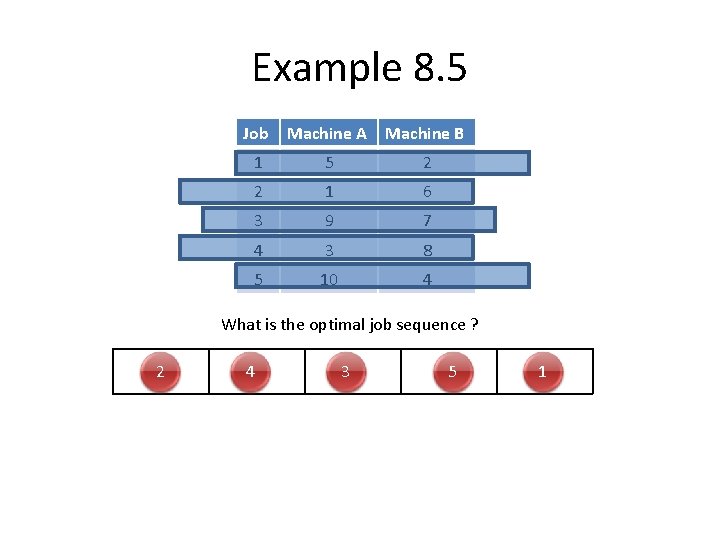
Example 8. 5 Job Machine A Machine B 1 5 2 2 1 6 3 9 7 4 3 8 5 10 4 What is the optimal job sequence ? 2 4 3 5 1

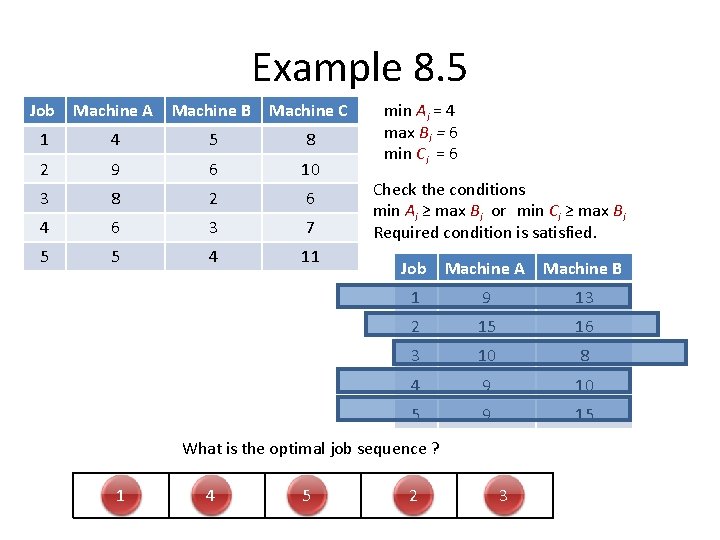
Extension to three machines • The problem of scheduling jobs on three machines is considerably more complex. • The three machine problem can be reduced to a two machine problem if the following condition is satisfied: – Label the machines A, B and C – Ai = Processing time of job i on machine A. (Bi , Ci are defined as similar) – min Ai ≥ max Bi or min Ci ≥ max Bi – Define Ai‘ = Ai + Bi and define Bi‘ = Bi + Ci

Example 8. 5 Job Machine A Machine B Machine C 1 4 5 8 2 9 6 10 3 8 2 6 4 6 3 7 5 5 4 11 min Ai = 4 max Bi = 6 min Ci = 6 Check the conditions min Ai ≥ max Bi or min Ci ≥ max Bi Required condition is satisfied. Job Machine A Machine B 1 9 13 2 15 16 3 10 8 4 9 10 5 9 15 What is the optimal job sequence ? 1 4 5 2 3

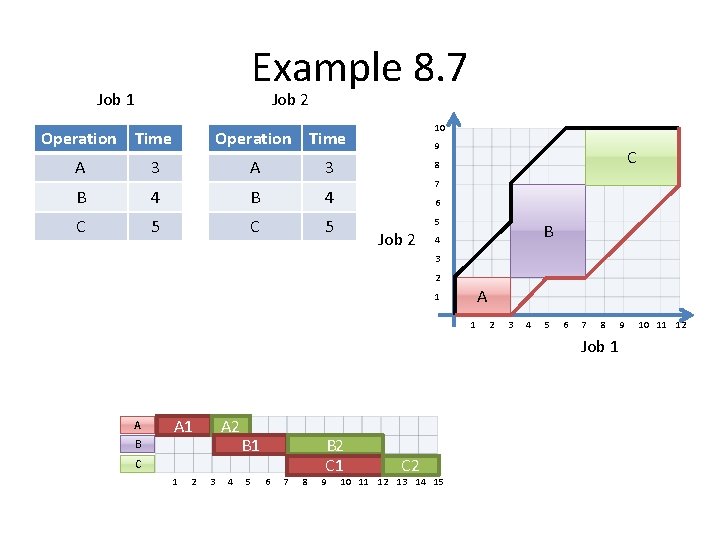
The two-shop Flow shop problem • Assume that two jobs are to be processed through m machines. • Each job must be processed by the machines in a particular order, but sequences for the two jobs need not to be the same. • A graphical procedure for solving this problem is developed by Aker (1954)

Aker’s Algorithm • Draw a Cartesian coordinate system. – Processing times for first job on the horizontal axis – Processing times for second job on the vertical axis – On each axis, mark off the operation times in the order in which the operations must be performed for that job. • Block out areas corresponding to each machine at the intersection of the intervals marked for that machine on the two axis. • Determine a path from origin to the end of final block that does not intersect any of the blocks and that minimizes the vertical movement.

Example 8. 7 Job 1 Job 2 Operation Time 10 Operation Time A 3 B 4 C 5 9 C 8 7 6 5 Job 2 B 4 3 2 A 1 1 2 3 4 5 6 7 8 Job 1 A A 1 A 2 B B 1 B 2 C 1 2 3 4 5 6 7 8 9 C 2 10 11 12 13 14 15 9 10 11 12