Sequences Linear Shift Registers and Stream Ciphers Tor

Sequences Linear Shift Registers and Stream Ciphers Tor Helleseth University of Bergen Norway

Outline - Motivation - Linear Feedback Shift Registers (LFSR) - Periodicity - Complexity - Nonlinear Feeedback Shift Registers - Applications to stream ciphers - Nonlinear generators - Filter generators - Clock controlled generators

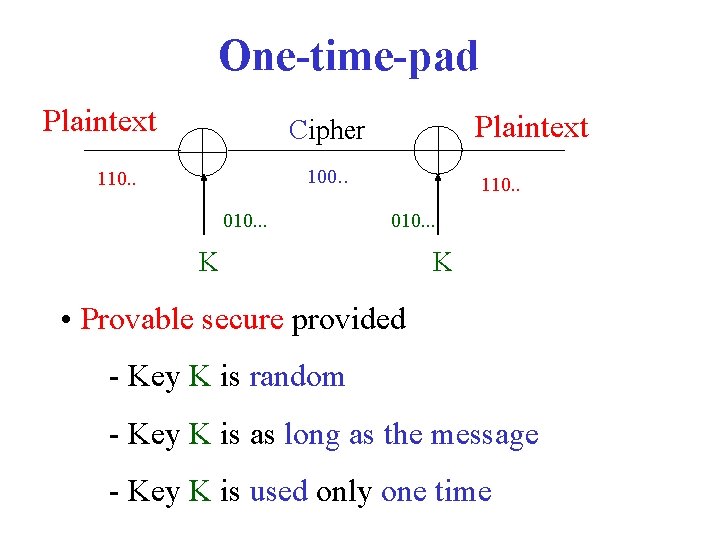
One-time-pad Plaintext Cipher 100. . 110. . 010. . . K K • Provable secure provided - Key K is random - Key K is as long as the message - Key K is used only one time

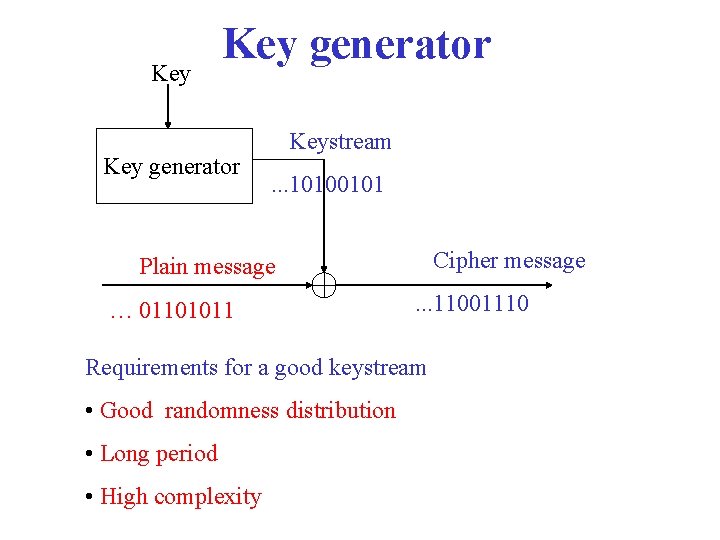
Key generator Keystream. . . 10100101 Cipher message Plain message … 01101011 . . . 11001110 Requirements for a good keystream • Good randomness distribution • Long period • High complexity

Generation of Keystream For a good system one needs: • Linearity - To control the period of keystream - To control randomness of keystream • Nonlinearity - To control complexity of keystream • Combination of linearity and nonlinearity - To also get good randomness and preserve the period and complexity

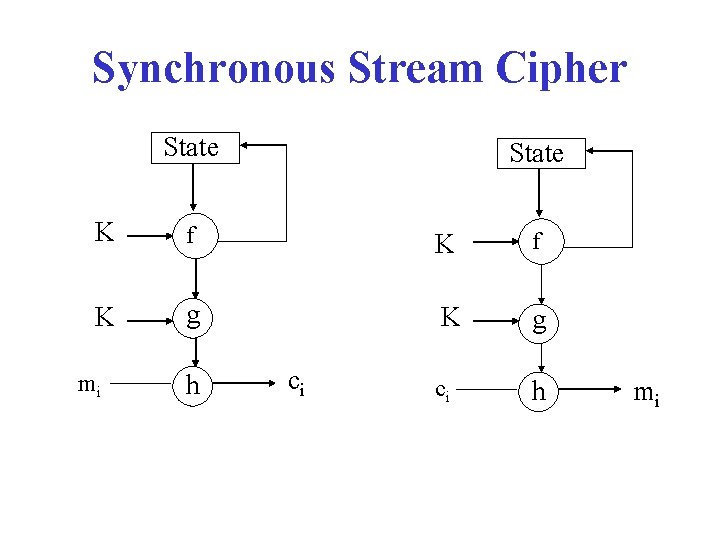
Synchronous stream cipher • Keystream is generated independent of the plaintext (and the ciphertext) - Initial state: σ0 (depends on key K) - Next state function: σi = f(σi-1, K) - Keystream function: … zi = g(σi, K) - Output function: ci = h(zi, mi) (In additive stream cipher: ci = zi + mi (mod 2)) • Needs synchronization between sender and receiver • No error propagation

Synchronous Stream Cipher State K f K g ci h mi h ci mi

Self-Synchronous Stream Cipher • Keystream is generated from the key and a fixed number of previous ciphertext symbols - Initial state: σ0 (depends on key K) - Next state function: σi=f(ci-1, ci-2, …, ci-T, K) - Keystream function: … zi=g(σi, K) - Output function: ci=h(zi, mi) (In additive stream cipher: ci = zi + mi (mod 2)) • Self synchronization • Limited error propagation

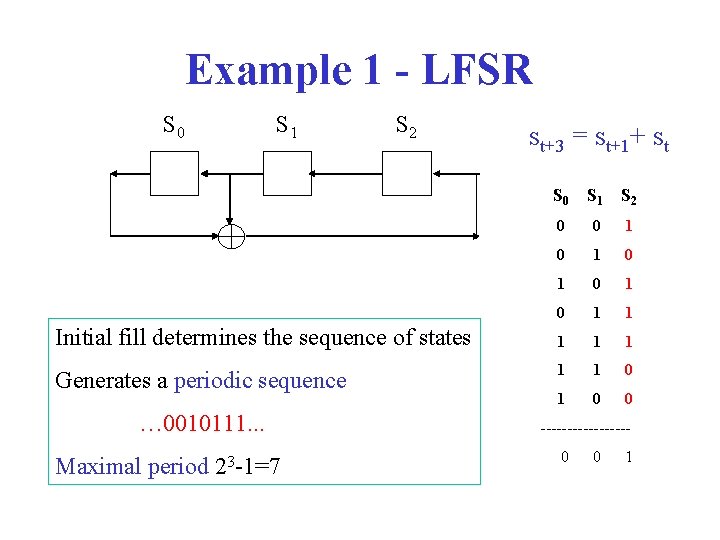
Difference Equation S 0 st+3 = st+1+st S 1 (mod 2) S 2 (t=0, 1, 2…) s 3 = s 1+s 0 s 4 = s 2+s 1 …………… Initial value of s 0, s 1, s 2 and the difference equation determines (st)

Example 1 - LFSR S 0 S 1 S 2 Initial fill determines the sequence of states Generates a periodic sequence … 0010111. . . Maximal period 23 -1=7 st+3 = st+1+ st S 0 S 1 S 2 0 0 1 0 1 0 1 1 1 1 0 0 --------0 0 1

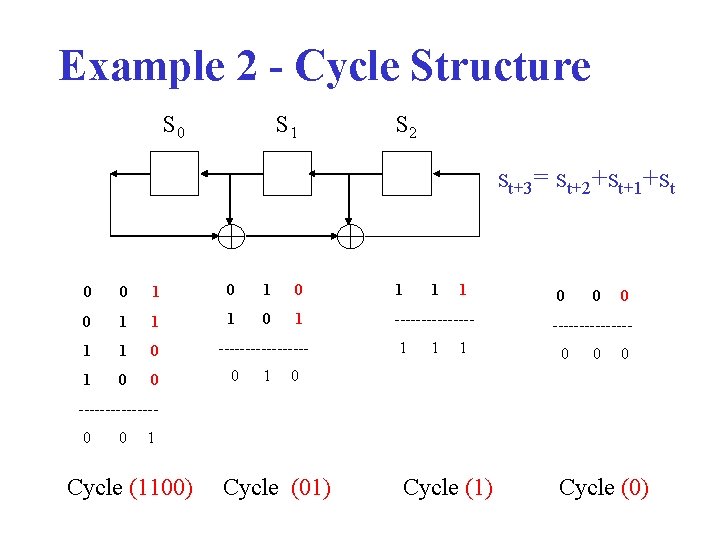
Example 2 - Cycle Structure S 0 S 1 S 2 st+3= st+2+st+1+st 0 0 1 0 1 1 1 0 1 -------- 1 1 0 0 --------0 1 1 1 0 0 0 --------------0 0 1 Cycle (1100) Cycle (01) Cycle (0)

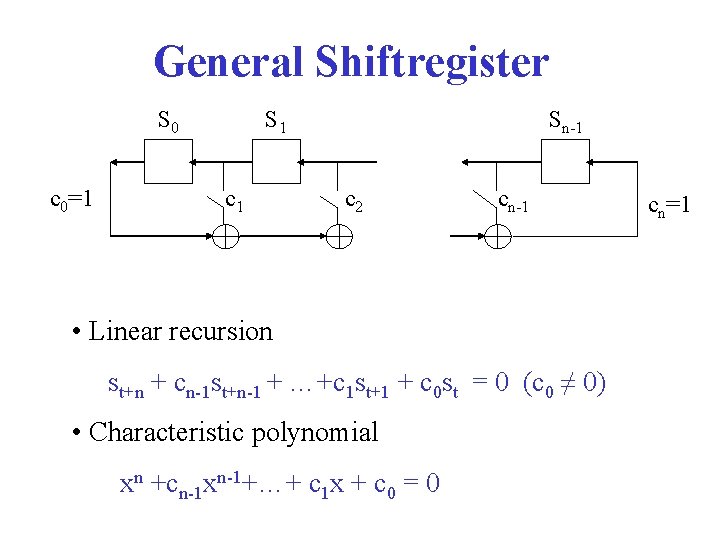
General Shiftregister S 0 c 0=1 S 1 c 1 Sn-1 c 2 cn-1 • Linear recursion st+n + cn-1 st+n-1 + …+c 1 st+1 + c 0 st = 0 (c 0 ≠ 0) • Characteristic polynomial xn +cn-1 xn-1+…+ c 1 x + c 0 = 0 cn=1

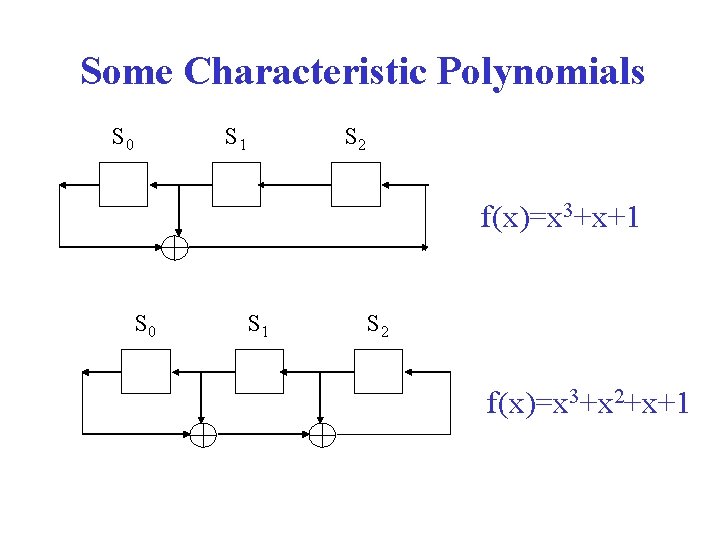
Some Characteristic Polynomials S 0 S 1 S 2 f(x)=x 3+x+1 S 0 S 1 S 2 f(x)=x 3+x 2+x+1

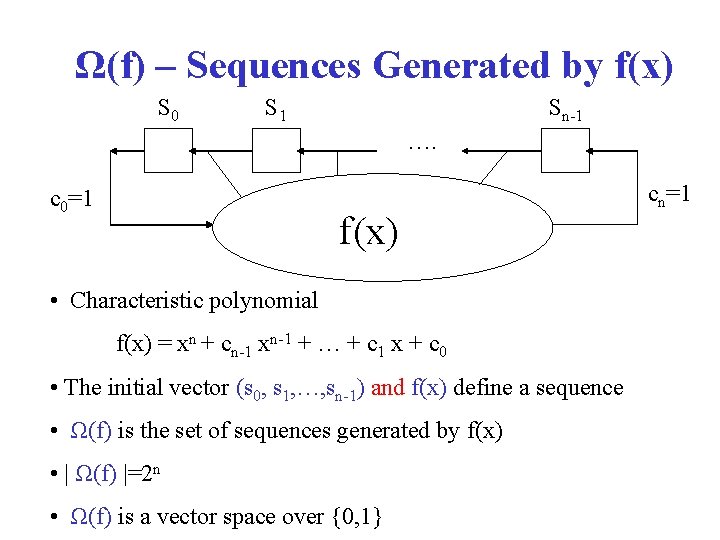
Ω(f) – Sequences Generated by f(x) S 0 S 1 Sn-1 …. c 0=1 f(x) • Characteristic polynomial f(x) = xn + cn-1 xn-1 + … + c 1 x + c 0 • The initial vector (s 0, s 1, …, sn-1) and f(x) define a sequence • Ω(f) is the set of sequences generated by f(x) • | Ω(f) |=2 n • Ω(f) is a vector space over {0, 1} cn=1

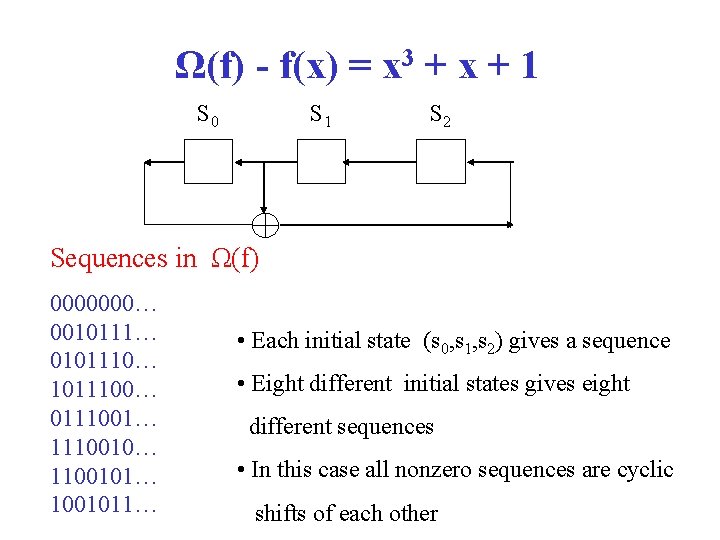
Ω(f) - f(x) = x 3 + x + 1 S 0 S 1 S 2 Sequences in Ω(f) 0000000… 0010111… 0101110… 1011100… 0111001… 1110010… 1100101… 1001011… • Each initial state (s 0, s 1, s 2) gives a sequence • Eight different initial states gives eight different sequences • In this case all nonzero sequences are cyclic shifts of each other

G(x) - Generating Function of a Sequence • Given a sequence s 0, s 1, s 2, … • Generating function ∞ G(x) = s 0+s 1 x+s 2 x 2+ s 3 x 3+ …= Σ si xi i=0 • First Fundamental Identity - Let (st) be a sequence in Ω(f) - Then (due to recursion most terms disappear) G(x) f*(x) = φ*(x) where φ(x)=s 0 xn-1+(s 1+cn-1 s 0)xn-2+(s 2+cn-1 s 1+cn-2 s 0)xn-3+… + (sn-1+cn-1 sn-2+…+c 1 s 0) and f*(x) is the reciprocal polynomial of f(x)

Example – First Fundamental Identity • (0010111) is generated by f(x) = x 3 + x + 1 • Generating function G(x) = x 2+x 4+x 5+x 6 + x 9+x 11+x 12+x 13 + x 16+… • What is φ(x) ? φ(x) = s 0 xn-1+(s 1+cn-1 s 0)xn-2 + (s 2+cn-1 s 1+cn-2 s 0)xn-3+… + (sn-1+cn-1 sn-2+…+c 1 s 0) =1 • G(x) = x 2/(x 3+x 2+1) = x 2+x 4+x 5+x 6 + x 9+x 11+x 12+x 13 + x 16+…

G(x) – When (st) is Periodic • Let (st) be periodic of period ε • Generating function G(x) = (s 0+s 1 x+…+sε-1 xε-1 ) (1 + xε + x 2ε + x 3ε +…) = (s 0+s 1 x+s 2 x 2+… +sε-1 xε-1 ) /(1 -xε ) = σ*(x)/(1 -xε ) • Combining with first fundamental identity gives G(x) = σ*(x)/(1 -xε ) = φ*(x)/f*(x) • Second Fundamental Identity (xε -1) φ(x) = σ(x) f(x) where - (st) periodic of period ε - φ(x) =s 0 xn-1+(s 1+cn-1 s 0)xn-2+…+ (sn-1+cn-1 sn-2+…+c 1 s 0) - σ(x) =s 0 xε-1+s 1 xε-2+…+ sε-1 - f(x) =xn+cn-1 xn-1+…+c 0

Example – Second Fundamental Identity • (0010111) is generated by f(x) = x 3 + x + 1 • Generating function - σ(x) = 1+x+x 2+x 4 - φ(x) = 1 - ε=7 • Second Fundamental Identity (xε -1) φ(x) = σ(x) f(x) (x 7+1)· 1 = (1+x+x 2+x 4)(x 3+x+1)

Period of f(x) Definition The period of the polynomial f(x) is the smallest integer e such that f(x) divides xe-1 Theorem Let (st) be a sequence in Ω(f) then (i) per(st) divides e=per(f) (ii) There is at least one (ut) in Ω(f) with period e=per(f)

Period of f(x) and Sequences in Ω(f) Proof: (i) Note that f(x) F(x) = xe-1 for some F(x). The first fundamental identity gives G(x) = φ*(x)/f*(x) = φ*(x)F*(x)/f*(x)F*(x) = φ*(x)F*(x)/(1 -xe) which implies (st) in Ω(f) repeats with period e (i. e. , ε ≤ e) (ii) From the second fundamental identity (xε -1) φ(x) = σ(x) f(x) Select φ(x) =1 then f(x) | xε -1 Hence, ε ≥ e and a sequence in Ω(f) with φ(x) =1 has period e

Cycle structure of Ω(f) - f(x) irreducible Theorem Let (st) be a nonzero sequence in Ω(f) where f(x) is irreducible. Then per(st) = per(f) = e Proof: Note that (xε -1) φ(x) = σ(x) f(x) and f(x) is irreducible Then, since gcd(φ(x), f(x))=1, then f(x) | xε -1 and therefore ε ≥e Hence, from the previous theorem ε =e

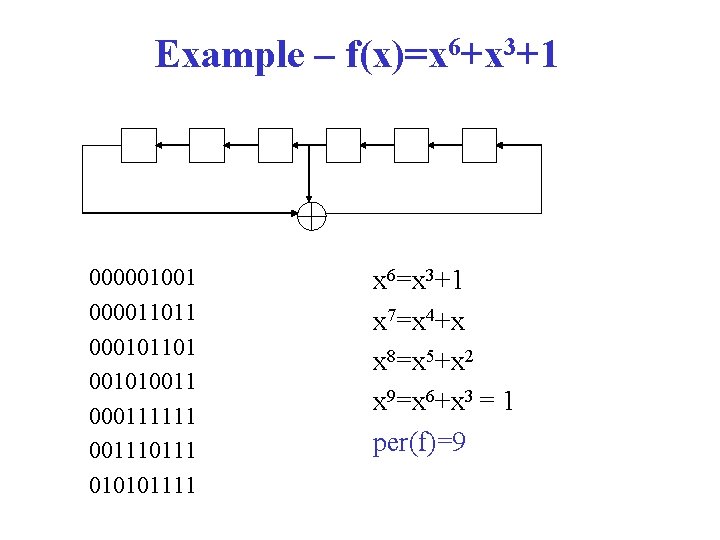
Example – f(x)=x 6+x 3+1 000001001 000011011 000101101 001010011 000111111 00111 010101111 x 6=x 3+1 x 7=x 4+x x 8=x 5+x 2 x 9=x 6+x 3 = 1 per(f)=9

Classical Method • Linear recursion st+n + cn-1 st+n-1 + …+c 1 st+1 + c 0 st = 0 (c 0 ≠ 0) • Characteristic polynomial xn +cn-1 xn-1+…+ c 1 x + c 0 = 0 • If all zeros of f(x) are simple, then st = Σ a i α i t where αi, i=1, 2, … are the zeros of f(x)

Example Recursion: st+3 = st+1+ st Characteristic polynomial: f(x) = x 3 + x +1 Let α 3 = α+1, then 1 α α 2 1 100 α 010 α 2 0 0 1 α 3 α 4 110 011 α 5 1 1 1 α 6 1 0 1 • Zeros of f(x) are α, α 2, α 4 • Then st = αt + α 2 t + α 4 t (st) = (1001011)

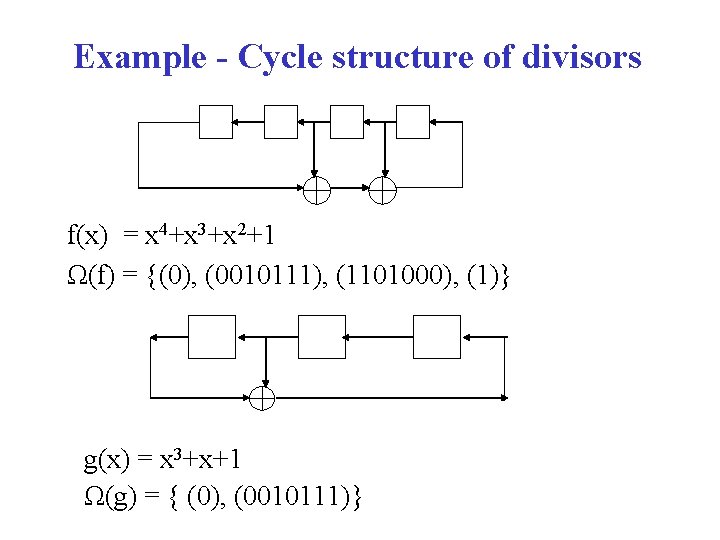
Example - Cycle structure of divisors f(x) = x 4+x 3+x 2+1 Ω(f) = {(0), (0010111), (1101000), (1)} g(x) = x 3+x+1 Ω(g) = { (0), (0010111)}

Some properties 1. Ω(f) + Ω(g) = Ω(lcm{f, g}) 2. Ω(f) ∩ Ω(g) = Ω(gcd{f, g})

Determining cycle structure of Ω(f) • Let f(x) = Πi fi(x)ki , fi(x) irreducible • To determine cycle structure of Ω(f) then 1. Determine the cycle structure of Ω(fi(x)ki) from the cycle structure (period) of fi(x) 2. Determine the cycle structure of Ω(gh) given the cycle structure of Ω(f) and Ω(f)

Cycle structure of Ω(fk) – f irreducible Theorem Let f(x) be irreducible of degree n and period e Determine κ such that 2κ < k ≤ 2κ+1 Then Ω(f) contains the following number of sequences with the following periods k : 1 2 4 … k κn n 2 n n 4 n 2 n … kn 2 k k-1 #Seq(Ω(f )Ω(f )) : 1 2 -2 Period : 1 e 2 e 4 e … 2κ+1 e

Examples (I) Example 1 • f(x)=x 2+x+1, n=2, e=3 #Sequences 1 Period 1 #Cycles 1 • Ω(f)={(0), (011)} 3 3 1 Example 2 • f(x) = (x 2+x+1)2, n=2, e=3 #Sequences 1 3 12 Period 1 3 6 #Cycles 1 1 2 • Ω(f)={(0), (011), (000101), (001111)}

Examples (II) Example 3 • f(x) = (x+1)k, n=1, e=1 k #New Sequences Period #Cycles 2 2 2 1 3 4 4 1 4 5 8 16 4 8 2 2 6 7 8 9 32 64 128 256 8 8 8 16 4 8 16 16

Structure of Ω(gh) – gcd(g, h)=1 Theorem Let gcd(g, h)=1 i. e. , Ω(gh) = Ω(g) Ω(h). Then any sequence in Ω(gh) can be uniquely written as a sum of a sequence in Ω(g) and one in Ω(h) Proof: Since gcd(g, h) = 1 then Ω(g) + Ω(h) = Ω(gh). and the result follows since |Ω(g)| |Ω(h)| = |Ω(gh)|.

Period of sequences Ω(gh) – gcd(g, h)=1 Theorem Let gcd(g, h)=1. Let (ut) Ω(f) and (vt) Ω(g). Then per((ut)+(vt)) = lcm{per(ut), per(vt)} Proof: Let τ be smallest integer such that (ut+ τ) + (vt+ τ) = (ut) + (vt) Hence, (ut+ τ) + (ut) = (vt+ τ) + (vt) Ω(f) ∩ Ω(g) = {(0)} Therefore, per(ut) | τ and per(vt) | τ which implies τ = lcm(per(ut), per(vt))

Cycle structure of Ω(gh) – gcd(g, h)=1 • • Let gcd(g, h)=1 then Ω(gh) = Ω(g) Ω(h) Let Ω(g) contain d 1 cycles of length λ 1, [d 1(λ 1)] Let Ω(h) contain d 2 cycles of length λ 2 , [d 2(λ 2)] Combine by adding the corresponding sequences #Sequences : d 1λ 1 d 2λ 2 Period : lcm{λ 1 , λ 2} #Cycles : d 1 d 2(λ 1, λ 2) Formally (cycle structure found combining all cycles and formulae) [d 1(λ 1)] [d 2(λ 2)] = [d(λ)] where d = d 1 d 2(λ 1, λ 2) λ = lcm{λ 1 , λ 2}

Exercises Exercise 1 • Let f(x)=(x 2+x+1)(x+1)2 • Determine the cycle structure of Ω(f) Exercise 2 • Let f(x)=(x+1)2(x 3+x+1)(x 4+x 3+x 2+x+1) • Determine the cycle structure of Ω(f)

Solution: Exercise 1 Let f(x) = (x 2+x+1)(x+1)2 • g(x) = x 2+x+1, Ω(g) : [1(1)+1(3)] • h(x) = (x+1)2 , Ω(h) : [2(1)+1(2)] The cycle structure of Ω(f) is [2(1)+1(2)+2(3)+1(6)] In fact, Ω(f) contains the cycles (000111), (001), (01), (1), (0)

Solution: Exercise 2 Let f(x) =x 15+x 14+x 13+x 9+x 3+1 = (x+1)2(x 3+x+1)3(x 4+x 3+x 2+x+1)=f 1(x)2 f 2(x)2 f 3(x) where • f 1(x) = x+1 Ω(f 1) : [2(1)] • f 2(x) = x 3+x+1 Ω(f 2) : [1(1)+1(7)] • f 3(x) = x 4+x 3+x 2+x+1 Ω(f 3) : [1(1)+3(5)] The cycle structure is • Ω(f 12) : [2(1)+1(2)] • Ω(f 23) : [1(1)+1(7)+4(14)+16(28)] • Ω(f 3) : [1(1)+3(5)] Combining gives cycle structure of Ω(f) [2(1)+1(2)+2(7)+17(14)+64(28)+6(5)+3(10)+6(35)+51(70)+192(40)]

Maximal Sequences • The maximal period of a sequence generated by a polynomial f(x) of degree n is at most 2 n-1 • f(x) is said to be primitive if f(x) is irreducible of degree n and period 2 n-1 Then f(x) generates a maximal sequence of period 2 n-1 • Some primitive polynomials and m-sequences - f(x) = x 3+x+1 (0010111) - f(x) = x 4+x+1 (000100110101111) - f(x) = x 5+x 2+1 (000010010110011111000110101)

Correlation of Sequences • Let (at) and (bt) be binary sequences of period • The crosscorrelation between (at) and (bt) at shift is -1 at+ - bt a, b( ) = (-1) t=0 • The autocorrelation of (at) at shift is -1 at+ - at a, a( ) = (-1) t=0

Two-level autocorrelation of m-sequences • Let (st) be an m-sequence of period =2 n-1 • Then the autocorrelation of the m-sequence is s, s( ) = 2 n-1 if =0 (mod 2 n-1) = -1 if 0 (mod 2 n-1) Proof: Let 0 (mod pn-1). Then s, s( ) = t (-1)st+ -st = t (-1) = -1 (since m-sequence is balanced) st+

Berlekamp-Massey algorithm • Can determine the minimum polynomial f(x)=xn+cn-1 xn-1+. . . +c 0 of a sequence (st) from 2 n successive bits s 0, s 1, …, s 2 n-1 s 0, s 1, …, sn-1 c 0 sn s 1, s 2, …, sn c 1 sn+1 ……………. . … sn-1, sn, …, s 2 n-2 cn-1 = … s 2 n-1 • Matrix has rank n if minimum polynomial has rank n • There exists a very efficient algorithm due to Berlekamp and Massey to calculate c 0, c 1, …, cn-1 in O(n 2) operations

Nonlinear Shiftregisters • • Increases linear complexity of keystream Difficult to predict the period No general theory exists Often one combines linear shiftregisters and nonlinear shiftregisters to control period and complexity

Golomb’s Randomness Postulates • Run = Consecutive 0’s or 1’s • Block =Runs of 1’s • Gap = Runs of 0’s • R 1. The number of zeros and number of ones differ by at most one during a period of the sequence. • R 2. Half of the runs in a full cycle have length 1, one 1/4 of all runs have length 2, 1/8 have length 3 etc, as long as the number of runs exceed one. Moreover, for each of these length there are equally many gaps and blocks. • R 3. The out of phase autocorrelation of the sequence always has the same value • Note: m-sequences obey and are the model for these postulates

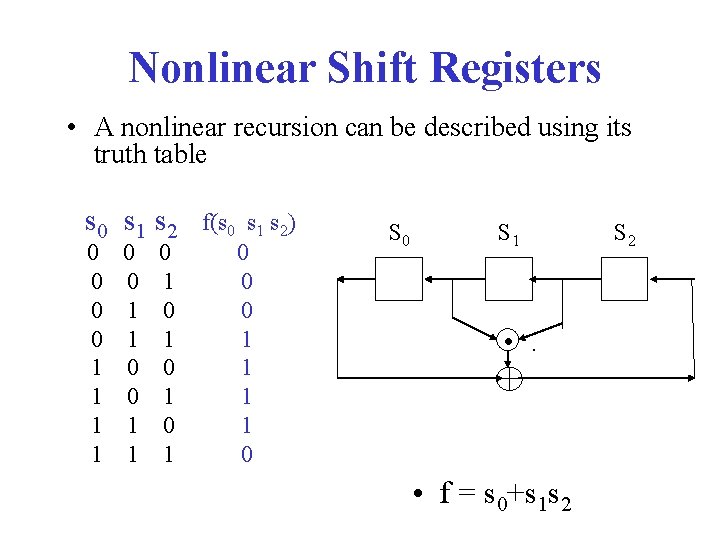
Nonlinear Shift Registers • A nonlinear recursion can be described using its truth table s 0 s 1 s 2 0 0 0 1 1 1 0 0 1 1 1 f(s 0 s 1 s 2) 0 0 0 1 1 0 S 1 • f = s 0+s 1 s 2 S 2

Nonlinear Functions s 0 s 1 s 2 f(s 0 s 1 s 2) 0 0 0 1 1 1 0 0 1 1 1 0 0 1 0 • How to find f(s 0, s 1, s 2) from a given truth table? • f(s 0 , s 1, s 2)=(1+s 0)(1+s 1)(1+s 2) + (1+s 0)(1+s 1)s 2 + (1+s 0)s 1 s 2 + s 0 s 1(1+s 2) = 1+ s 0+s 1 s 2 • # Boolean functions in n-variable 22 n • # Boolean linear functions in n-variable 2 n

Table look up (Multiplexing) Can construct complex cryptographic transformations by table look-up x 1 … xn-1 xn. . . 0 … 0 0 y 0 0 … 0 1 y 1 ………. . 1 … 1 1 … y 2 n-1 (n=3) F = y 0 (x 1+1)(x 2+1)(x 3+1)+ y 1(x 1+1)(x 2+1)x 3+…+ y 7 x 1 x 2 x 3

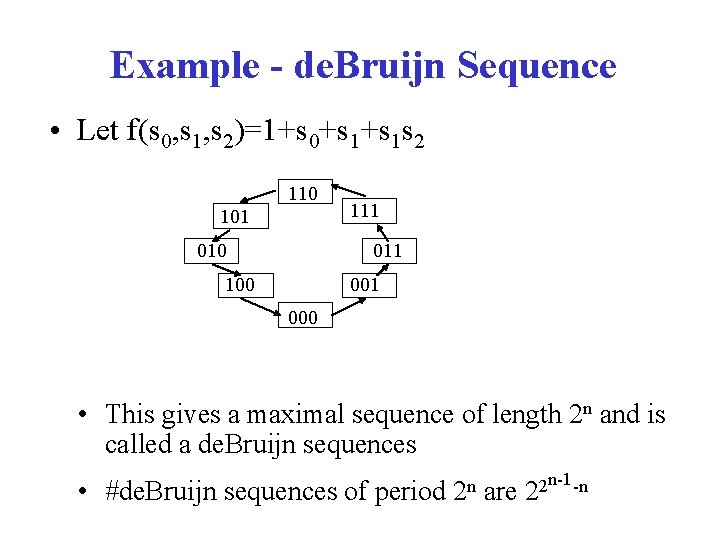
Example - de. Bruijn Sequence • Let f(s 0, s 1, s 2)=1+s 0+s 1 s 2 110 101 010 111 011 100 001 000 • This gives a maximal sequence of length 2 n and is called a de. Bruijn sequences n-1 -n • #de. Bruijn sequences of period 2 n are 22

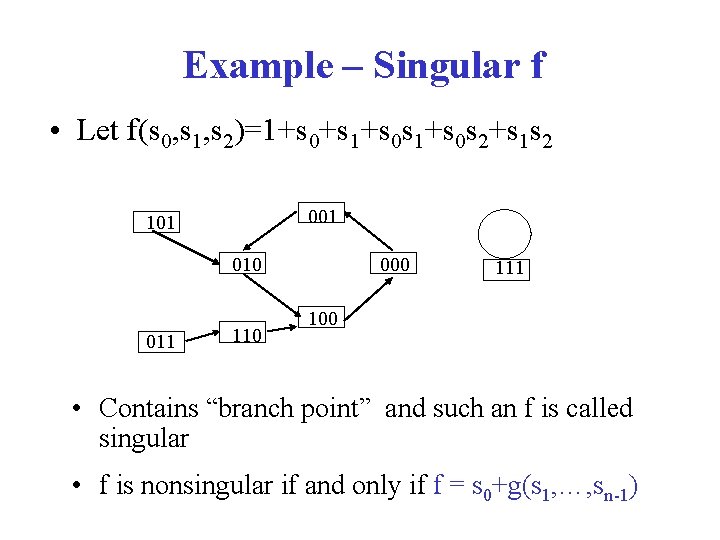
Example – Singular f • Let f(s 0, s 1, s 2)=1+s 0+s 1+s 0 s 2+s 1 s 2 001 101 010 011 110 000 111 100 • Contains “branch point” and such an f is called singular • f is nonsingular if and only if f = s 0+g(s 1, …, sn-1)

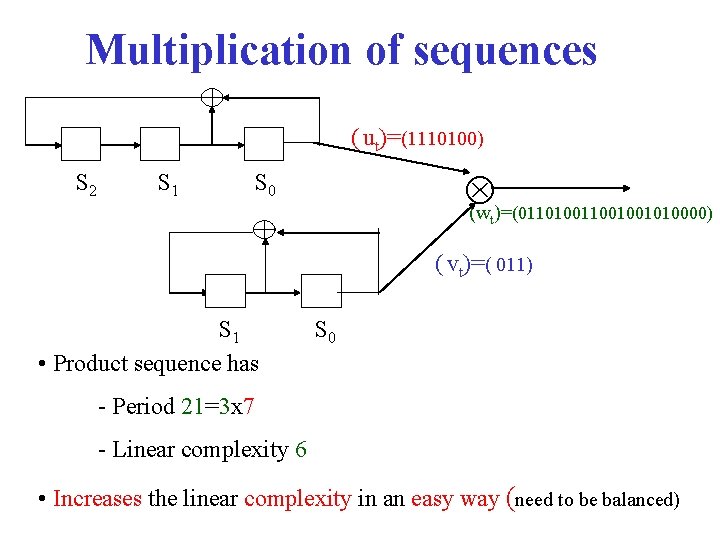
Multiplication of sequences ( ut)=(1110100) S 2 S 1 (w )=(01101001001010000) S 0 t ( vt)=( 011) S 1 • Product sequence has S 0 - Period 21=3 x 7 - Linear complexity 6 • Increases the linear complexity in an easy way (need to be balanced)

Period of (utvt) Theorem Let gcd(per(ut), per(vt))=1 then per(utvt) = per(ut)·per(vt) Proof: If per(utvt) ≠ per(ut)·per(vt) then per(utvt) = k·per(ut) where k | per(vt). Decimate (utvt) by e=per(ut) gives (u 0 v 0), (u 0 ve), (u 0 v 2 e), … of period k< per(vt). Since, gcd(e, per(vt))=1 this is a contradiction.

Linear Complexity of (utvt) • Let (ut) Ω(f) and (vt) Ω(g) • Let (wt) = (ut vt) ut = Σ ai αit where αi zeros of f(x) vt = Σ bj βjt where βj zeros of g(x) Then (wt) = Σ ai bj αit βjt If h(x) has all products αi βj as zeros then (wt) Ω(h)

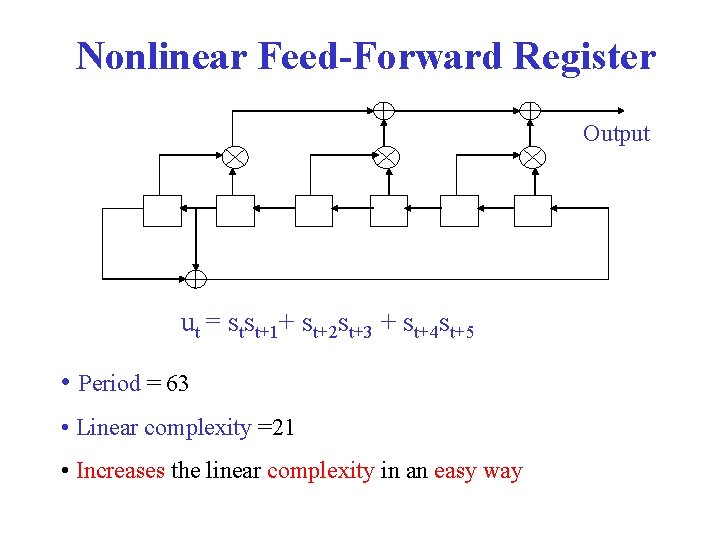
Nonlinear Feed-Forward Register Output ut = stst+1+ st+2 st+3 + st+4 st+5 • Period = 63 • Linear complexity =21 • Increases the linear complexity in an easy way

Properties of a Filter Generator Let (st) be an m-sequence of period 2 n-1 Let ut = st+τst+2τ…st+kτ n Then the linear complexity of (ut) is ( ) k N Let zt = Σ ci st+i+δ…st+i+(k-1)δ i=0 Then the linear complexity of (zt) is when at least one ci is nonzero n ( k )–(N-1)

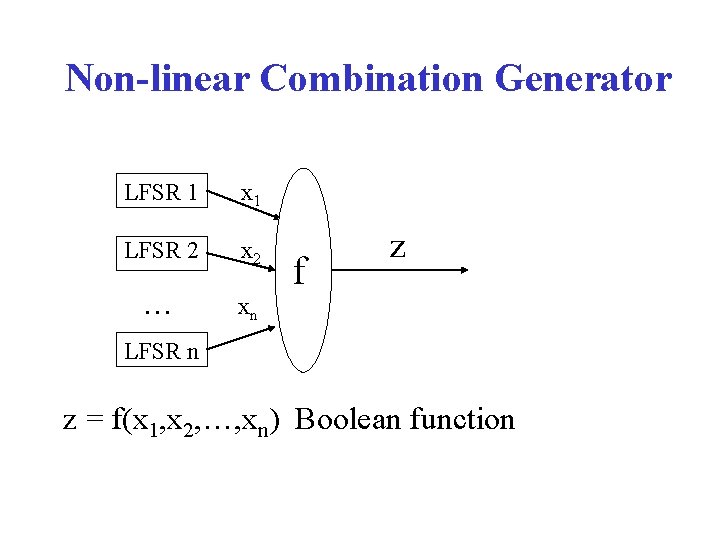
Non-linear Combination Generator LFSR 1 x 1 LFSR 2 x 2 … xn f z LFSR n z = f(x 1, x 2, …, xn) Boolean function

Linear Complexity LFSR 1 x 1 LFSR 2 x 2 … LFSR n • • • f z x 2 Let LFSR i generate m-sequence of period 2 Li-1 Let gcd(Li, Lj) = 1 for all i ≠ j Let Li ≥ 2 for all i Let f(x 1, …, xn) = Σ a. IXI (XI=xi 1. . xit ) Then linear complexity is f(L 1, …, Ln)

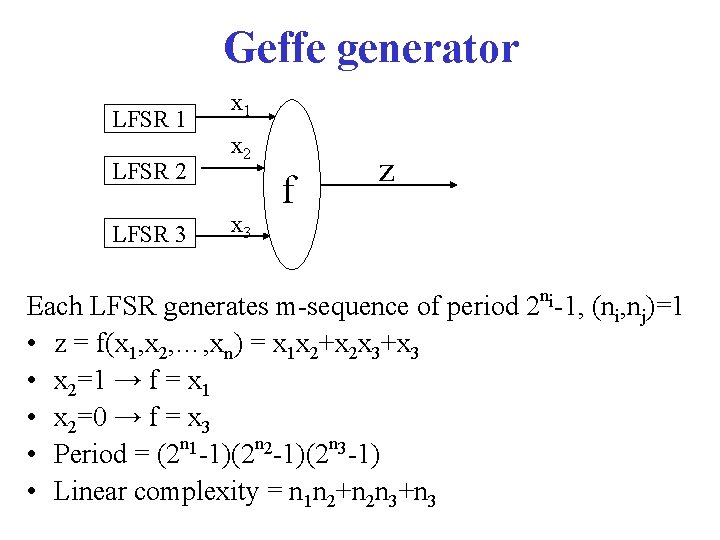
Geffe generator LFSR 1 LFSR 2 LFSR 3 x 1 x 2 x 3 f z Each LFSR generates m-sequence of period 2 ni-1, (ni, nj)=1 • z = f(x 1, x 2, …, xn) = x 1 x 2+x 2 x 3+x 3 • x 2=1 → f = x 1 • x 2=0 → f = x 3 • Period = (2 n 1 -1)(2 n 2 -1)(2 n 3 -1) • Linear complexity = n 1 n 2+n 2 n 3+n 3

Correlation attack - Geffe generator LFSR 1 LFSR 2 LFSR 3 x 1 x 2 x 3 f z Correlation attack of Geffe generator (NB! Prob(z=x 1)=¾) - Guess initial state of LFSR 1 - Compare x 1 and z - If agreement ¾ , guess is likely to be correct - If agreement ½ , guess is likely to be wrong

Cascade Coupling LFSR A (at) LFSR B (ct) • Output sequence 0… 0 1 0 … = a c = a b =0… 0 b 0 0… 0 b 10… 0 b 2 0…. = (ct) • For two m-sequences (at) and (bt) of period 2 m-1 the cascaded sequence has - Period: (2 m-1)2 - Linear complexity: m(2 m-1) • Randomness - Probability of 1 is approximately ¼ - Can get a probability ½ by adding suitable combinations

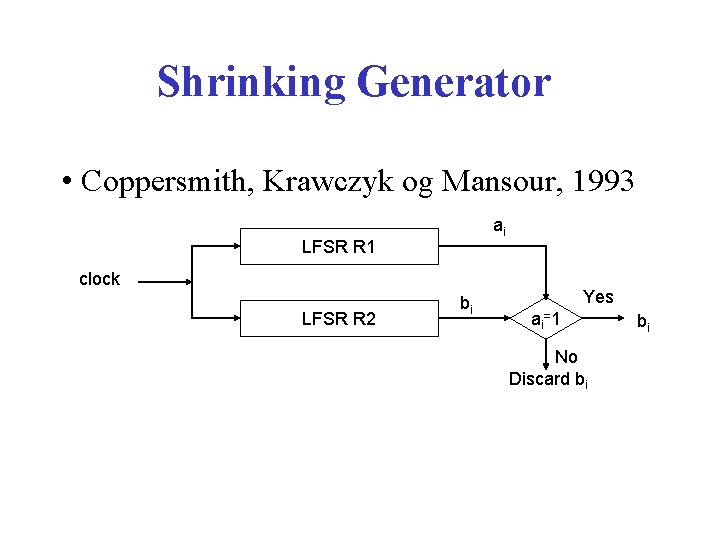
Shrinking Generator • Coppersmith, Krawczyk og Mansour, 1993 ai LFSR R 1 clock LFSR R 2 bi Yes ai=1 No Discard bi bi

Properties • If gcd(L 1, L 2) = 1, the period will be (2 L 2 -1)2 L 1 -1 • Linear complexity L is bounded by – L 22 L 1 -2 < L 22 L 1 -1 • Statistical properties in the output sequence is “almost” uniform • Security level of the generator is “approximately” 22 L, i. e. selecting length of R 1 and R 2 close to 64, gives 128 bits “security”

From LFSR to stream cipher • Non-linear combining – Output from several LFSR as input to a non-linear function • Non-linear filtering – Read content of several cells in an LFSR with a non-linear function • Clock-controlled generator – Let LFSR control the clocking of another LFSR that generates the key stream • Multiplexing LFSR 2 LFSR 1 Multiplexer ki