Sequences Linear Foundation GCSE Questions AQA These questions

Sequences – Linear – Foundation – GCSE Questions – AQA These questions are the same format as previous GCSE exams. COPY means they use the exact same numbers as the original GCSE question. Otherwise, they are clone questions using different numbers. The worksheets are provided in 2 sizes.

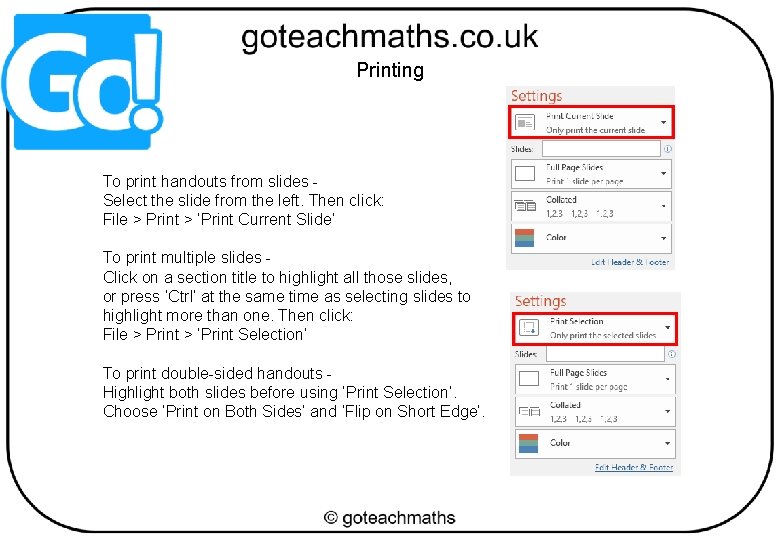
Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

AQA Foundation: June 2017 Paper 2, Q 15 1 Here are some numbers. 1 4 4 9 14 AQA Foundation: June 2017 Paper 2, Q 15 8 9 14 20 Here are some numbers. 24 4 is an arithmetic progression. 4 Use three of the numbers to make a different arithmetic progression. Describe the rule. [2 marks] 9 14 Here are some numbers. 24 is an arithmetic progression. 14 AQA Foundation: June 2017 Paper 2, Q 15 1 4 8 9 14 20 Here are some numbers. 24 is an arithmetic progression. Use three of the numbers to make a different arithmetic progression. Describe the rule. [2 marks] 4 4 9 14 8 9 14 20 24 is an arithmetic progression. Use three of the numbers to make a different arithmetic progression. Describe the rule. [2 marks] Answer Rule 20 Rule AQA Foundation: June 2017 Paper 2, Q 15 9 14 Answer Rule 4 9 Use three of the numbers to make a different arithmetic progression. Describe the rule. [2 marks] Answer 1 8 Answer Rule

AQA Foundation: June 2017 Paper 2, Q 4 1 1 [1 mark] 2 [1 mark]

AQA Foundation: June 2018 Paper 3, Q 29 1 1 [3 marks] Answer

AQA Foundation: November 2017 Paper 1, Q 17 1 AQA Foundation: November 2017 Paper 1, Q 17 A sequence has three terms. The term-to-term rule for the sequence is 1 A sequence has three terms. The term-to-term rule for the sequence is multiply by 8 and then add 11 1 (a) The first term of the sequence is – 1 Work out the third term. multiply by 8 and then add 11 [2 marks] 1 (a) The first term of the sequence is – 1 Work out the third term. Answer 1 (b) The order of the three terms is reversed to make a new sequence. Work out the term-to-term rule for this sequence. Answer [2 marks] Answer [1 mark] 1 (b) The order of the three terms is reversed to make a new sequence. Work out the term-to-term rule for this sequence. Answer [1 mark]

AQA Foundation: November 2017 Paper 1, Q 17 1 A sequence has three terms. The term-to-term rule for the sequence is multiply by 8 and then add 11 1 (a) The first term of the sequence is – 1 Work out the third term. [2 marks] Answer 1 (b) The order of the three terms is reversed to make a new sequence. Work out the term-to-term rule for this sequence. Answer [1 mark]

AQA Foundation: November 2017 Paper 1, Q 17 1 A sequence has three terms. The term-to-term rule for the sequence is multiply by 8 and then add 11 1 (a) The first term of the sequence is – 1 Work out the third term. 1 st 2 nd 3 rd [2 marks] − 1 × 8 + 11 = 3 3 × 8 + 11 = 35 Answer 35 1 (b) The order of the three terms is reversed to make a new sequence. Work out the term-to-term rule for this sequence. 35 3 − 1 Reverse operations Answer Subtract 11, divide by 8 [1 mark]

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk