Sequence strategy cards in order from least sophisticated












- Slides: 15

� Sequence strategy cards in order from least sophisticated to most � List to the side the knowledge, skills and understandings a student would need to implement the strategy http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

Briefly review the Levels in the progressions document starting on page 25 � Level 1 – Making and counting all � Level 2 – Repeated counting by a given number � Level 3 – Use properties relational CC & and OA Progression document – pages 25 -26 thinking http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� For each level, identify at least 1 strategy card as a “clear example” of that level. � How does your group’s card sequence align with the levels described? � Do & OAof Progression you wish to move. CC any your document – pages 25 -26 strategy cards? Facilitating Teacher Growth for State-wide Student Success in http: //kentuckymathematics. org

http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� Sophistication of Unitizing Numbers � Distancing the Setting � Knowledge of Multiples and Sequences of Multiples � Development of Non-counting Strategies http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� Sophistication of Unitizing Numbers � Distancing the Setting � Knowledge of Multiples and Sequences of Multiples � Development of Non-counting Strategies http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

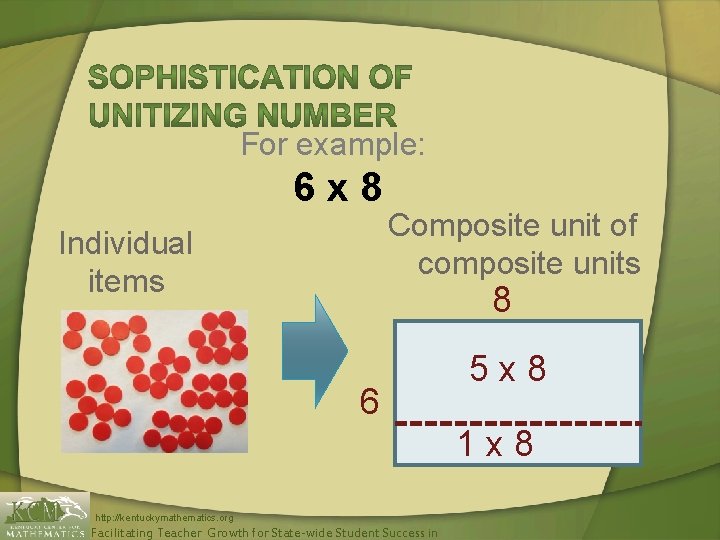
For example: 6 x 8 Individual items Composite unit of composite units 8 6 5 x 8 1 x 8 http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� Sophistication � Distancing of Unitizing Numbers the Setting 7 x 3 http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� Sophistication of Unitizing Numbers � Distancing the Setting � Knowledge of Multiples and Sequences of Multiples http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

� Sophistication of Unitizing Numbers � Distancing the Setting � Knowledge of Multiples and Sequences of Multiples � Development of Non-counting Strategies http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

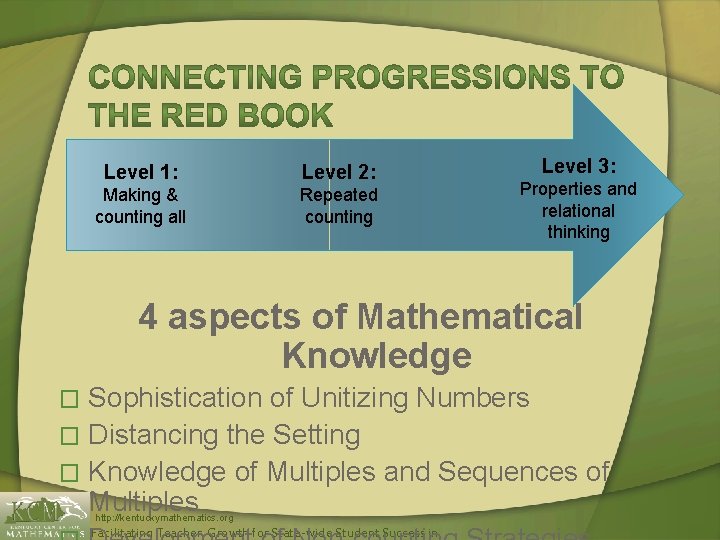
Level 1: Level 2: Making & counting all Repeated counting Level 3: Properties and relational thinking 4 aspects of Mathematical Knowledge Sophistication of Unitizing Numbers � Distancing the Setting � Knowledge of Multiples and Sequences of Multiples � http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

Level 1: Level 2: Making & counting all Repeated counting Level 3: Properties and relational thinking Why is it important for a child to “spend time” working at level 2? � How quickly can we expect a child to “move through” these levels? � How can we craft a classroom environment that support kids at their mathematical level AND encourages growth? � http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

http: //www 2. nzmaths. co. nz/Numeracy/ONPD/M 1/ 07. aspx http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in

http: //kentuckymathematics. org Facilitating Teacher Growth for State-wide Student Success in