Sequence Similarity The Viterbi algorithm for alignment Compute

Sequence Similarity

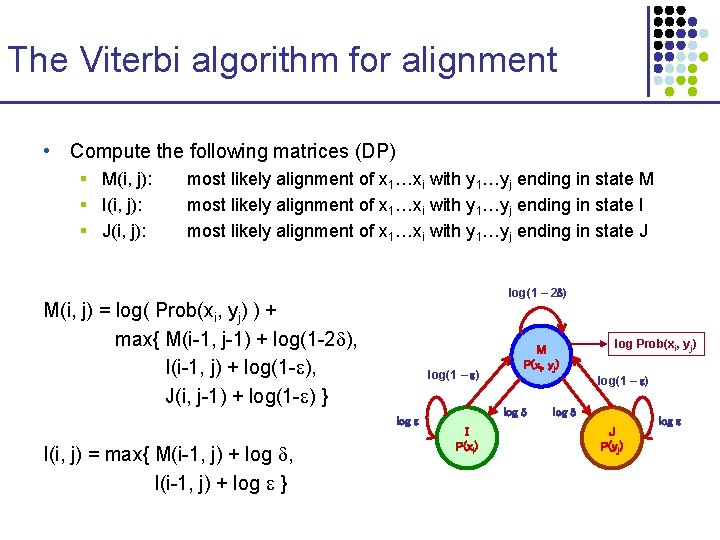
The Viterbi algorithm for alignment • Compute the following matrices (DP) § M(i, j): § I(i, j): § J(i, j): most likely alignment of x 1…xi with y 1…yj ending in state M most likely alignment of x 1…xi with y 1…yj ending in state I most likely alignment of x 1…xi with y 1…yj ending in state J log(1 – 2 ) M(i, j) = log( Prob(xi, yj) ) + max{ M(i-1, j-1) + log(1 -2 ), I(i-1, j) + log(1 - ), J(i, j-1) + log(1 - ) } log(1 – ) log I(i, j) = max{ M(i-1, j) + log , I(i-1, j) + log } M P(xi, yj) log(1 – ) log I P(xi) log Prob(xi, yj) log J P(yj) log

One way to view the state paths – State M y 1 x 1 …… xm …… yn

State I y 1 x 1 …… xm …… yn

State J y 1 x 1 …… xm …… yn

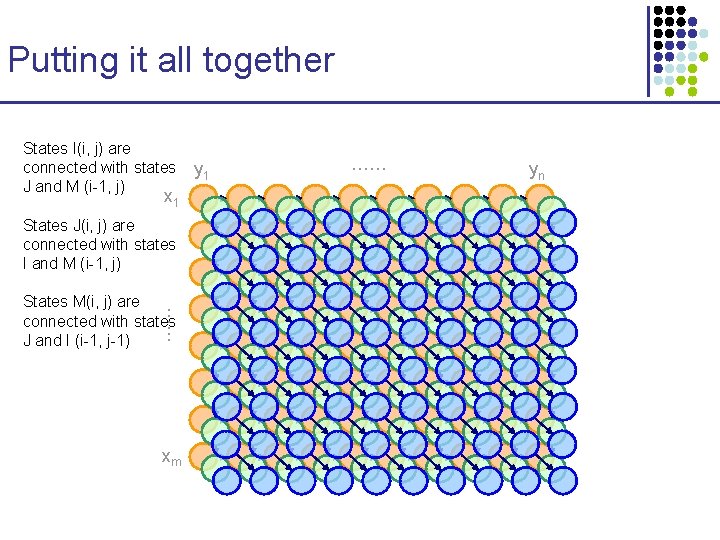
Putting it all together States I(i, j) are connected with states J and M (i-1, j) x 1 States J(i, j) are connected with states I and M (i-1, j) …… States M(i, j) are connected with states J and I (i-1, j-1) xm y 1 …… yn

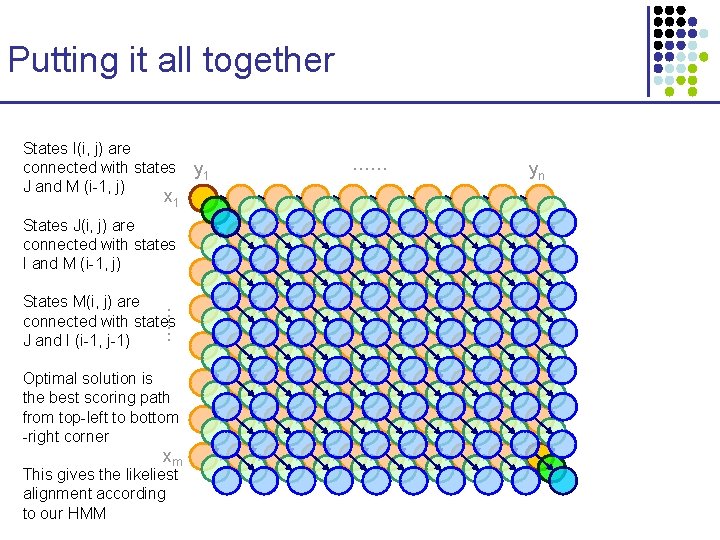
Putting it all together States I(i, j) are connected with states J and M (i-1, j) x 1 States J(i, j) are connected with states I and M (i-1, j) …… States M(i, j) are connected with states J and I (i-1, j-1) Optimal solution is the best scoring path from top-left to bottom -right corner xm This gives the likeliest alignment according to our HMM y 1 …… yn

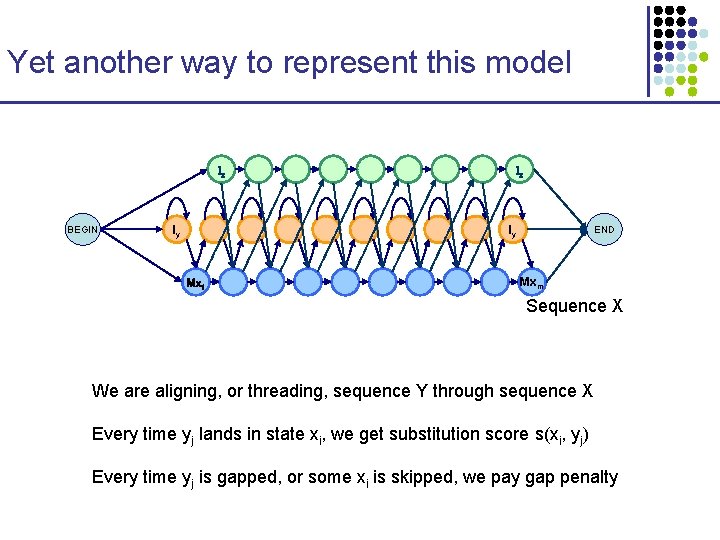
Yet another way to represent this model Ix BEGIN Iy Ix Iy Mx 1 END Mxm Sequence X We are aligning, or threading, sequence Y through sequence X Every time yj lands in state xi, we get substitution score s(xi, yj) Every time yj is gapped, or some xi is skipped, we pay gap penalty

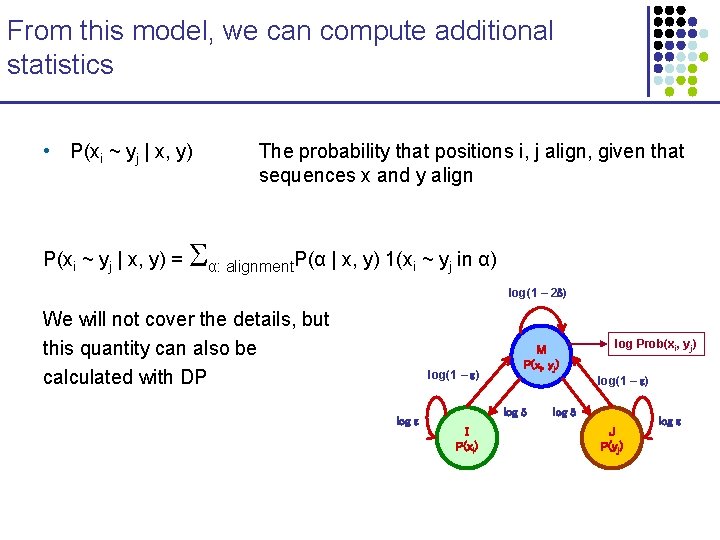
From this model, we can compute additional statistics • P(xi ~ yj | x, y) = The probability that positions i, j align, given that sequences x and y align α: alignment. P(α | x, y) 1(xi ~ yj in α) log(1 – 2 ) We will not cover the details, but this quantity can also be calculated with DP log(1 – ) log M P(xi, yj) log(1 – ) log I P(xi) log Prob(xi, yj) log J P(yj) log

Fast database search – BLAST (Basic Local Alignment Search Tool) Main idea: query 1. Construct a dictionary of all the words in the query 2. Initiate a local alignment for each word match between query and DB Running Time: O(MN) However, orders of magnitude faster than Smith-Waterman DB

BLAST Original Version • …… Dictionary: All words of length k (~11 nucl. ; ~4 aa) Alignment initiated between words of alignment score T (typically T = k) • Alignment: Ungapped extensions until score below statistical threshold • Output: All local alignments with score > statistical threshold query …… scan DB query

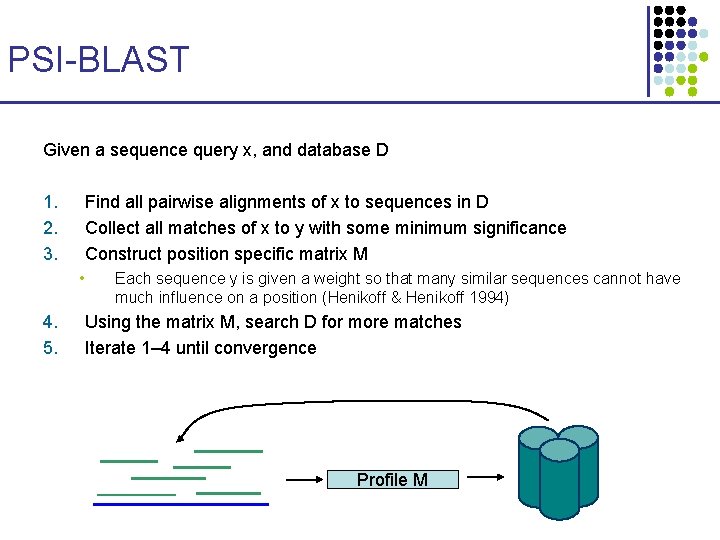
PSI-BLAST Given a sequence query x, and database D 1. 2. 3. Find all pairwise alignments of x to sequences in D Collect all matches of x to y with some minimum significance Construct position specific matrix M • 4. 5. Each sequence y is given a weight so that many similar sequences cannot have much influence on a position (Henikoff & Henikoff 1994) Using the matrix M, search D for more matches Iterate 1– 4 until convergence Profile M

BLAST Variants • • • BLASTN – genomic sequences BLASTP – proteins BLASTX – translated genome versus proteins TBLASTN – proteins versus translated genomes TBLASTX – translated genome versus translated genome PSIBLAST – iterated BLAST search http: //www. ncbi. nlm. nih. gov/BLAST

Multiple Sequence Alignments

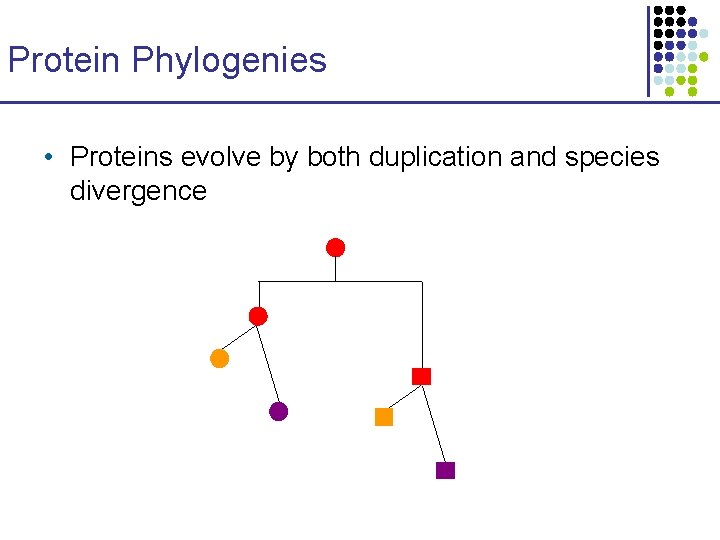
Protein Phylogenies • Proteins evolve by both duplication and species divergence

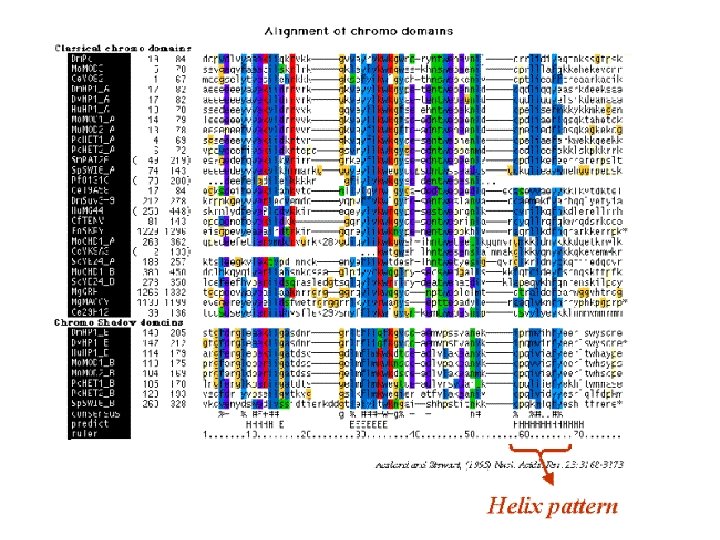
Definition • Given N sequences x 1, x 2, …, x. N: § Insert gaps (-) in each sequence xi, such that • All sequences have the same length L • Score of the global map is maximum • A faint similarity between two sequences becomes significant if present in many • Multiple alignments can help improve the pairwise alignments

Scoring Function: Sum Of Pairs Definition: Induced pairwise alignment A pairwise alignment induced by the multiple alignment Example: x: y: z: AC-GCGG-C AC-GC-GAG GCCGC-GAG Induces: x: ACGCGG-C; y: ACGC-GAC; x: AC-GCGG-C; z: GCCGC-GAG; y: AC-GCGAG z: GCCGCGAG

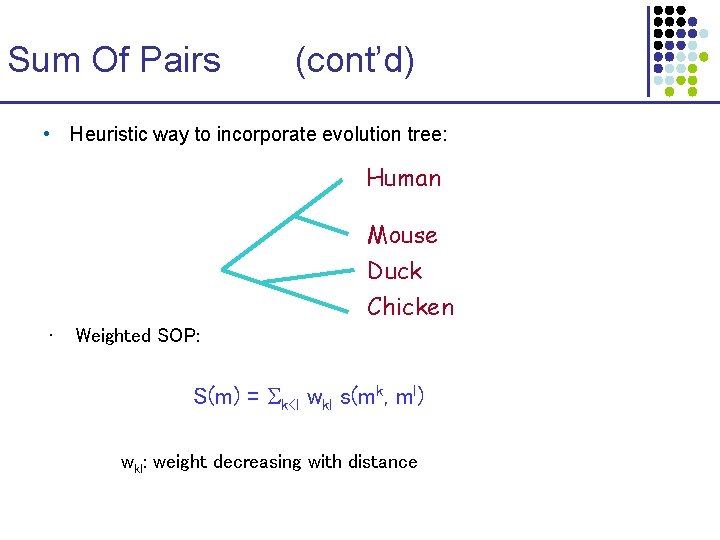
Sum Of Pairs (cont’d) • Heuristic way to incorporate evolution tree: Human Mouse Duck Chicken • Weighted SOP: S(m) = k<l wkl s(mk, ml) wkl: weight decreasing with distance

A Profile Representation T C C C A C G T - A A A G G G – – C C C T T T 1 A A A T C C T T 1 . 6 1 A A G . 4 1 C – – T G G G G . 4. 2. 4. 8. 4 1 . 6. 2. 2 1 C C C . 8 1. 2. 2. 2 C C C . 6 . 8 • Given a multiple alignment M = m 1…mn § Replace each column mi with profile entry pi • Frequency of each letter in • # gaps • Optional: # gap openings, extensions, closings § Can think of this as a “likelihood” of each letter in each position

Multiple Sequence Alignments Algorithms

Multidimensional DP Generalization of Needleman-Wunsh: S(m) = i S(mi) (sum of column scores) F(i 1, i 2, …, i. N): Optimal alignment up to (i 1, …, i. N) F(i 1, i 2, …, i. N) = max(all neighbors of cube)(F(nbr)+S(nbr))

Multidimensional DP • Example: in 3 D (three sequences): • 7 neighbors/cell F(i, j, k) = max{ F(i-1, j-1, k-1)+S(xi, xj, xk), F(i-1, j-1, k )+S(xi, xj, - ), F(i-1, j , k-1)+S(xi, -, xk), F(i-1, j , k )+S(xi, -, - ), F(i , j-1, k-1)+S( -, xj, xk), F(i , j-1, k )+S( -, xj, xk), F(i , j , k-1)+S( -, -, xk) }

Multidimensional DP Running Time: 1. Size of matrix: LN; Where L = length of each sequence N = number of sequences 2. Neighbors/cell: 2 N – 1 Therefore…………… O(2 N LN)

Multidimensional DP How do gap states generalize? Running • Time: badly! 1. Size • of. VERY matrix: L N; § Require 2 N states, one per combination of gapped/ungapped sequences Where L lengthtime: of each § = Running O(2 N sequence 2 N LN) = O(4 N LN) N = number of sequences Y YZ 2. Neighbors/cell: 2 N – 1 XY XYZ Z Therefore…………… O(2 N LN) X XZ

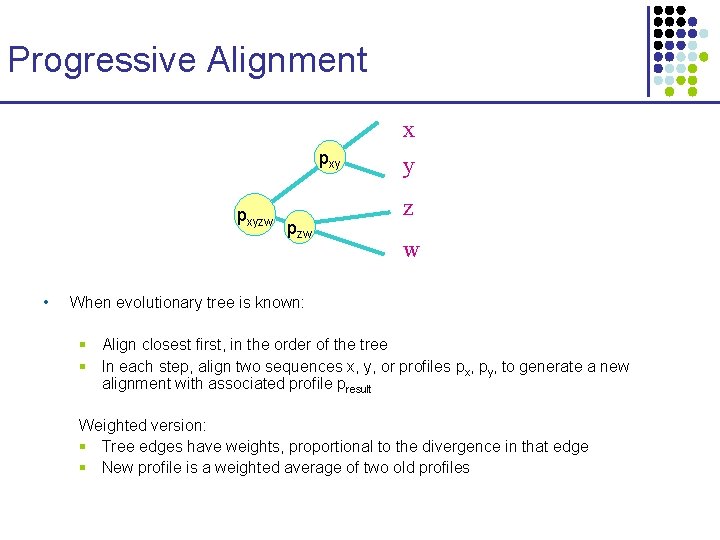
Progressive Alignment x pxyzw • pzw y z w When evolutionary tree is known: § Align closest first, in the order of the tree § In each step, align two sequences x, y, or profiles px, py, to generate a new alignment with associated profile presult Weighted version: § Tree edges have weights, proportional to the divergence in that edge § New profile is a weighted average of two old profiles

Progressive Alignment x y Example z Profile: (A, C, G, T, -) px = (0. 8, 0. 2, 0, 0, 0) w py = (0. 6, 0, 0. 4) • When evolutionary tree is known: s(px, py) = 0. 8*0. 6*s(A, A) + 0. 2*0. 6*s(C, A) + 0. 8*0. 4*s(A, -) + 0. 2*0. 4*s(C, -) § Align closest first, in the order of the tree § In each step, align two sequences. Result: x, y, or profiles px, py 0. 1, , to generate a new pxy = (0. 7, 0, 0, 0. 2) alignment with associated profile presult s(p , -) = 0. 8*1. 0*s(A, -) + 0. 2*1. 0*s(C, -) x Weighted version: § Tree edges have weights, proportional to the divergence in that edge Result: p = (0. 4, 0. 1, 0, 0, 0. 5) § New profile is a weighted average of two old x-profiles

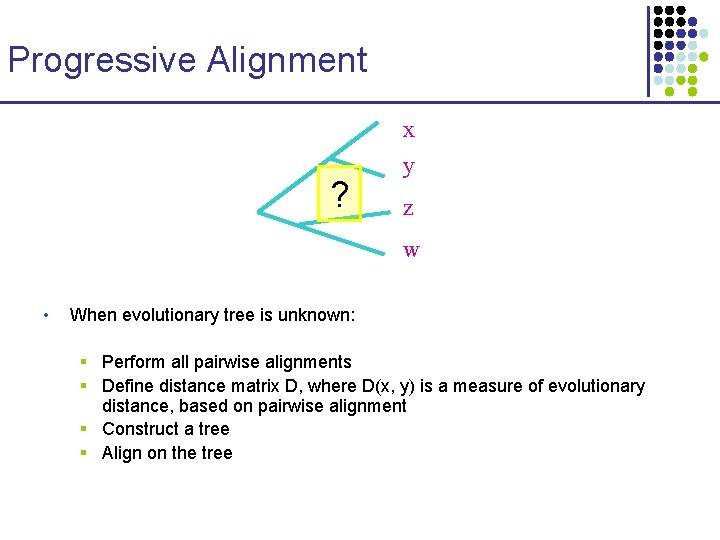
Progressive Alignment x ? y z w • When evolutionary tree is unknown: § Perform all pairwise alignments § Define distance matrix D, where D(x, y) is a measure of evolutionary distance, based on pairwise alignment § Construct a tree § Align on the tree

Heuristics to improve alignments • Iterative refinement schemes • A*-based search • Consistency • Simulated Annealing • …

Iterative Refinement One problem of progressive alignment: • Initial alignments are “frozen” even when new evidence comes Example: x: y: GAAGTT GAC-TT Frozen! z: w: GAACTG GTACTG Now clear correct y = GA-CTT

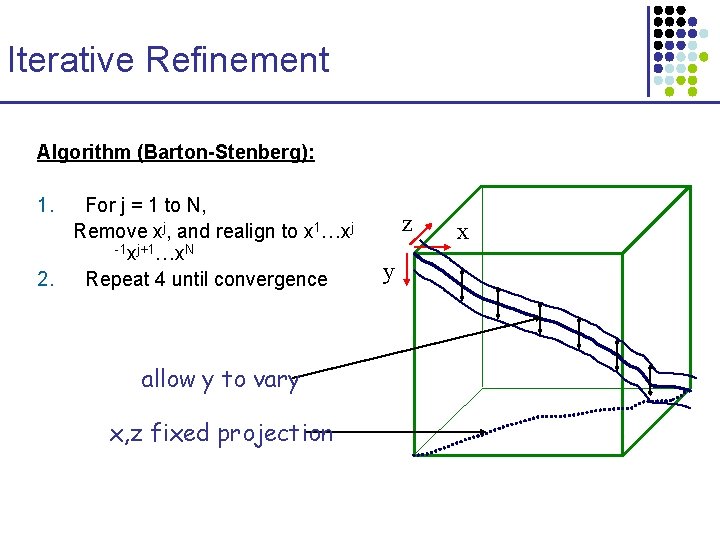
Iterative Refinement Algorithm (Barton-Stenberg): 1. For j = 1 to N, Remove xj, and realign to x 1…xj -1 xj+1…x. N 2. Repeat 4 until convergence allow y to vary x, z fixed projection z y x

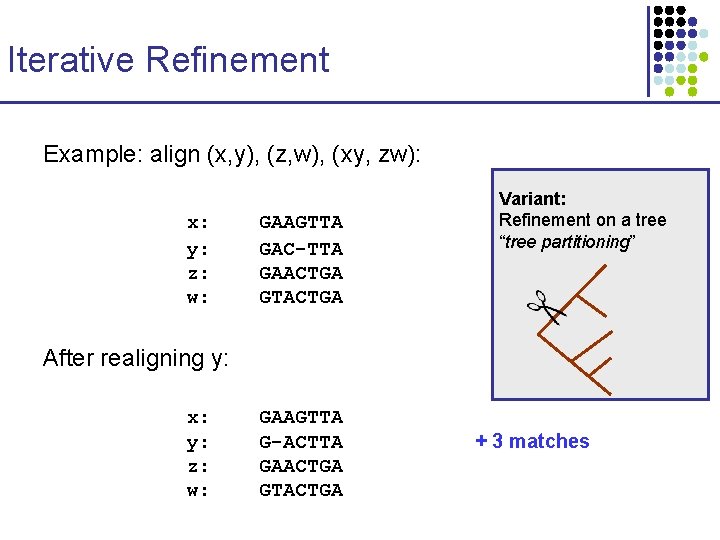
Iterative Refinement Example: align (x, y), (z, w), (xy, zw): x: y: z: w: GAAGTTA GAC-TTA GAACTGA GTACTGA Variant: Refinement on a tree “tree partitioning” After realigning y: x: y: z: w: GAAGTTA G-ACTTA GAACTGA GTACTGA + 3 matches

Iterative Refinement Example: align (x, y), (z, w), (xy, zw): x: y: z: w: GAAGTTA GAC-TTA GAACTGA GTACTGA After realigning y: x: y: z: w: GAAGTTA G-ACTTA GAACTGA GTACTGA + 3 matches

Iterative Refinement Example not handled well: x: y 1: y 2: y 3: GAAGTTA GAC-TTA z: w: GAACTGA GTACTGA Realigning any single yi changes nothing

Some Resources http: //www. ncbi. nlm. nih. gov/BLAST & PSI-BLAST http: //www. ebi. ac. uk/clustalw/ CLUSTALW – most widely used http: //phylogenomics. berkeley. edu/cgi-bin/muscle/input_muscle. py MUSCLE – most scalable http: //probcons. stanford. edu/ PROBCONS – most accurate

MUSCLE at a glance 1. Fast measurement of all pairwise distances between sequences • DDRAFT(x, y) defined in terms of # common k-mers (k~3) – O(N 2 L log. L) time 2. Build tree TDRAFT based on DDRAFT, with a hierarchical clustering method (UPGMA) 3. Progressive alignment over TDRAFT, resulting in multiple alignment MDRAFT 4. Measure distances D(x, y) based on MDRAFT 5. Build tree T based on D 6. Progressive alignment over T, to build M 7. Iterative refinement; for many rounds, do: • • Tree Partitioning: Split M on one branch and realign the two resulting profiles If new alignment M’ has better sum-of-pairs score than previous one, accept

xi yj MATCH INSERT X xi ― PROBCONS: Probabilistic Consistency-based Multiple Alignment of Proteins INSERT Y ― yj

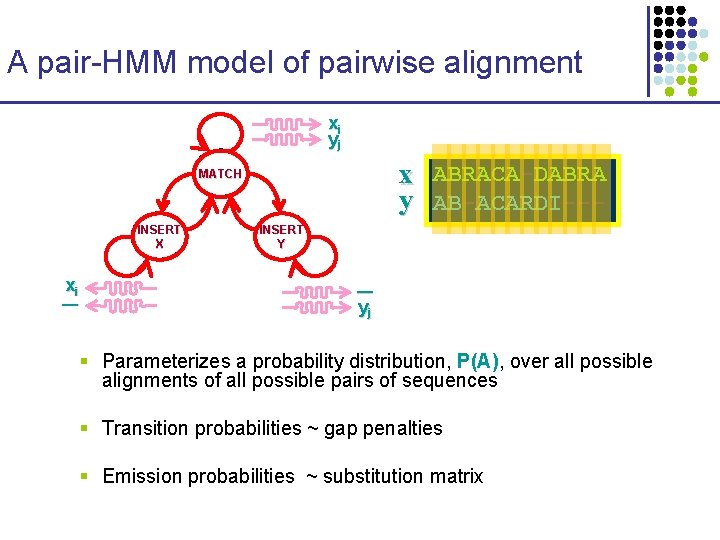
A pair-HMM model of pairwise alignment xi yj x ABRACA-DABRA y AB-ACARDI--- MATCH INSERT X xi ― INSERT Y ― yj § Parameterizes a probability distribution, P(A), over all possible alignments of all possible pairs of sequences § Transition probabilities ~ gap penalties § Emission probabilities ~ substitution matrix

Computing Pairwise Alignments P(α) αviterbi P(α | x, y) • The Viterbi algorithm § conditional distribution P(α | x, y) reflects model’s uncertainty over the “correct” alignment of x and y § identifies highest probability alignment, αviterbi, in O(L 2) time Caveat: the most likely alignment is not the most accurate § Alternative: find the alignment of maximum expected accuracy

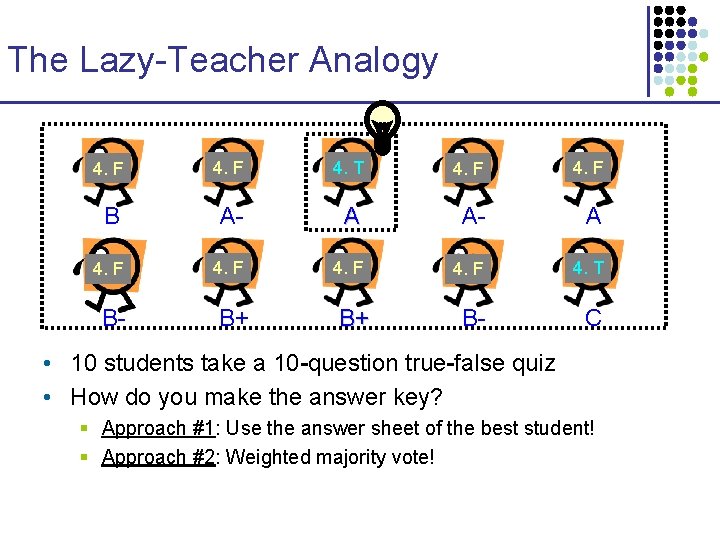
The Lazy-Teacher Analogy 4. F 4. T 4. F B A- A 4. F 4. T B- C B- B+ B+ • 10 students take a 10 -question true-false quiz • How do you make the answer key? § Approach #1: Use the answer sheet of the best student! § Approach #2: Weighted majority vote!

Viterbi vs. Maximum Expected Accuracy (MEA) Viterbi 4. T A Maximum Expected Accuracy 4. F 4. T 4. F B A- A 4. F 4. T B- C B- B+ B+ • picks single alignment with highest chance of being completely correct • picks alignment with highest expected number of correct predictions • mathematically, finds the alignment α that maximizes Eα*[1{α = α*}] • mathematically, finds the alignment α that maximizes Eα*[accuracy(α, α*)]