Sequence Homology M M Dalkilic Ph D Monday














- Slides: 16

Sequence Homology M. M. Dalkilic, Ph. D Monday, September 08, 2008 Class II Indiana University, Bloomington, IN 1 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Outline �Sword of Damocles Lab I ? Skeptica Due l �New Reading Posted on Website �New Lab II / Homework Posted on Website �Readings [Mount] Chap 3, [R] Chaps 3 -4 �Most Important Aspect of Bioinformatics— homology search through sequence similarity 2 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Outline (cont’d) �Sequence Similarity o Most common Bioinformatics tool in use o One of the most misunderstood tools in use o Requires a great deal of background in ancillary disciplines —especially computation 3 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Outline (cont’d) �Computational Elements of Sequence Similarity o Algorithms o Complexity o Recursion & recurrence relations o Program strategies to reduce complexity of algorithms • Divide and Conquer • Dynamic Programming Sequence Similiarty (Computation) M. M. 4 Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

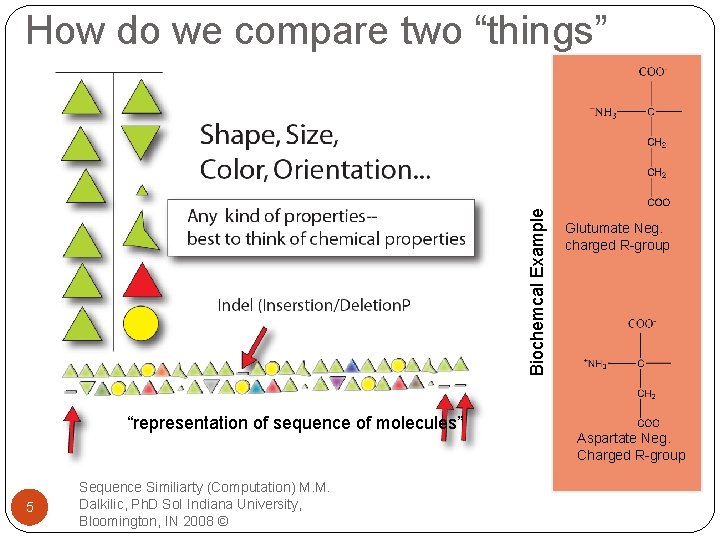
Biochemcal Example How do we compare two “things” “representation of sequence of molecules” 5 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 © Glutumate Neg. charged R-group Aspartate Neg. Charged R-group

Computation Algorithm “process or rules for (esp. machine) calculations. The execution of an algorithm must not include any subjective decisions, nor must it require the use of intuition or creativity” [Brassard & Bratley] 6 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation Algorithm When we set out to solve a problem, it is important to decide…on (1) size of the instances (2) representation (3) time/memory considerations 7 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation Algorithm (1) Size of the instances (2) Representation (3) Time/Memory considerations 8 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

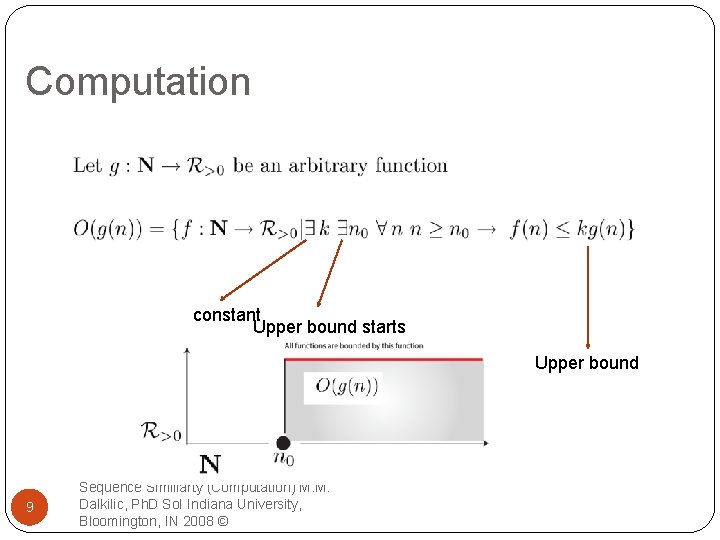
Computation constant Upper bound starts Upper bound 9 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation 10 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation Recurrence relations—relations defined by (1) initial point (2) recursive (self-depreciation) 11 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation 12 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation Though every recursive program can be written as as a while 13 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation 14 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation 15 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©

Computation (Next Lecture) Divide and Conquer gives rise to Dynamic Programming—the approach used in sequence comparison 16 Sequence Similiarty (Computation) M. M. Dalkilic, Ph. D So. I Indiana University, Bloomington, IN 2008 ©