Sequence analysis of nucleic acids and proteins part

Sequence analysis of nucleic acids and proteins: part 2 Prediction of structure and function Based on Chapter 3 of Post-genome bioinformatics by Minoru Kanehisa Oxford University Press, 2000

Search and learning problems in sequence analysis

Thermodynamic principle The amino acid sequence contains all the information necessary to fold a protein molecule into its native 3 D state under physiological conditions: fold, denature, spontaneously refold, called Anfinsen’s thermodynamic principle Thus it should be possible to predict 3 D structure computationally by minimizing a suitable conformational energy function, but difficult to define, difficult to minimize (globally), called ab initio In practice, structures determined by X-ray crystallography and nuclear magnetic resonance (NMR) are used to give empirical structure-function relationships.

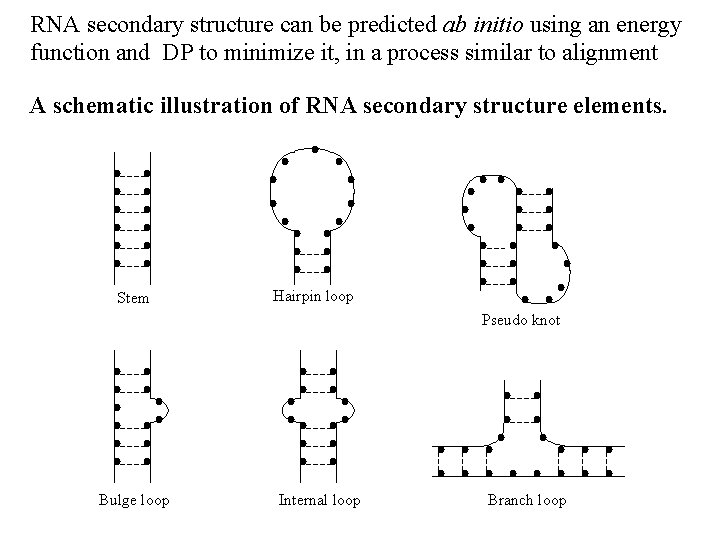
RNA secondary structure can be predicted ab initio using an energy function and DP to minimize it, in a process similar to alignment A schematic illustration of RNA secondary structure elements. Stem Hairpin loop Pseudo knot Bulge loop Internal loop Branch loop

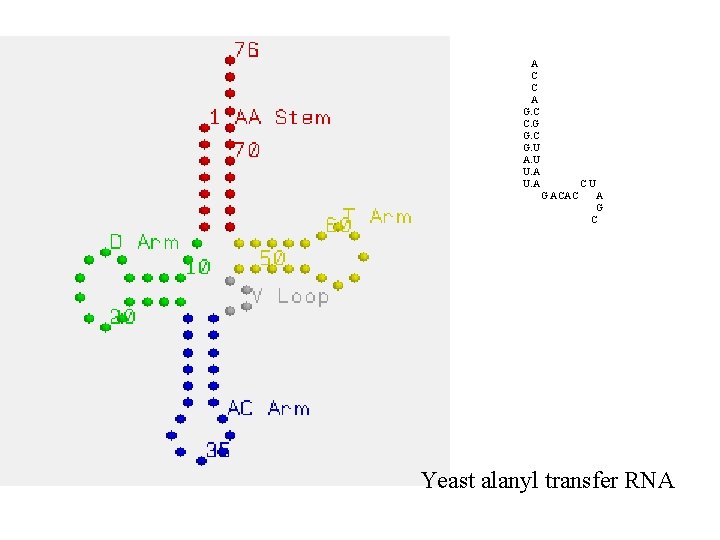
A C C A G. C C. G G. C G. U A. U U. A G ACAC CU A G C Yeast alanyl transfer RNA

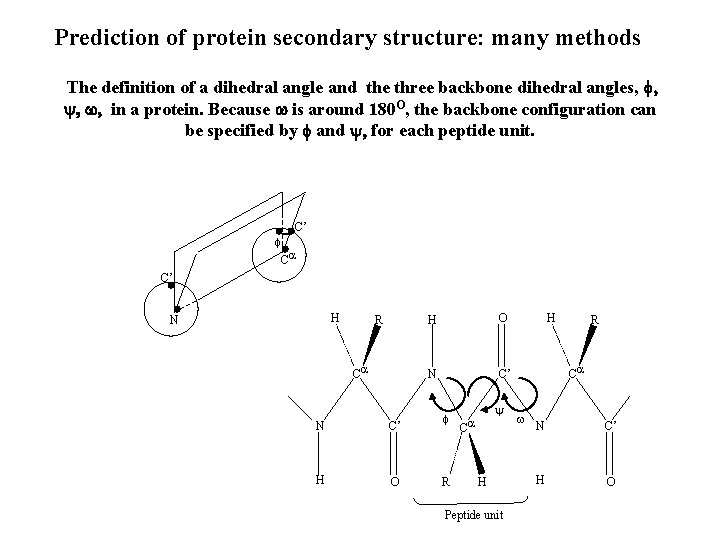
Prediction of protein secondary structure: many methods The definition of a dihedral angle and the three backbone dihedral angles, f, y, w, in a protein. Because w is around 180 O, the backbone configuration can be specified by f and y, for each peptide unit. f C’ C C’ H N R C N C’ H O N C’ f R y C H Peptide unit H R C w N C’ H O

Prediction of protein secondary structure The options are -helix, -strand coil. Many 2º structure prediction methods exist, with ones by Chou-Fasman and another due to Garnier, Osguthorpe and Robson being widely used. These are position&structurespecific scoring matrices based on modest or large numbers of proteins. On the next page we display the GOR PSSM for -helices. These days one can choose from methods based on almost every major machine learning approach: ANN, HMM, etc.

Cter Helix State Nter

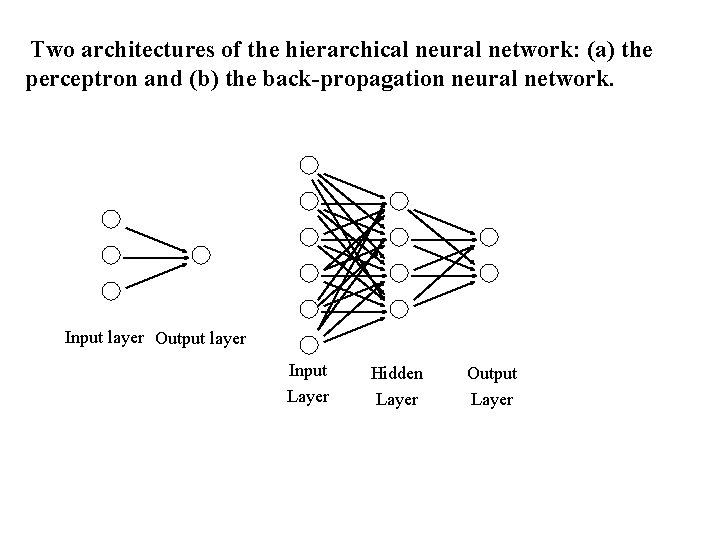
Two architectures of the hierarchical neural network: (a) the perceptron and (b) the back-propagation neural network. Input layer Output layer Input Layer Hidden Layer Output Layer

Prediction of transmembrane domains Membrane proteins are very common, perhaps 25% of all. Membranes are hydrophobic and so a transmembrane domain typically has hydrophobic residues, about 20 to span the membrane. There a number of rules for detecting them: Kyte. Doolittle hydropathy scores work fairly well, and the Klein-Kanehisa-De. Lisi discriminant function does even better.

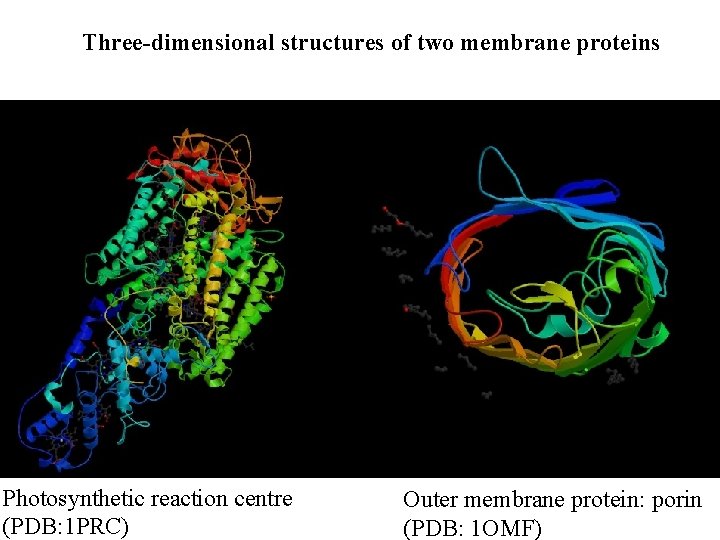
Three-dimensional structures of two membrane proteins Photosynthetic reaction centre (PDB: 1 PRC) Outer membrane protein: porin (PDB: 1 OMF)

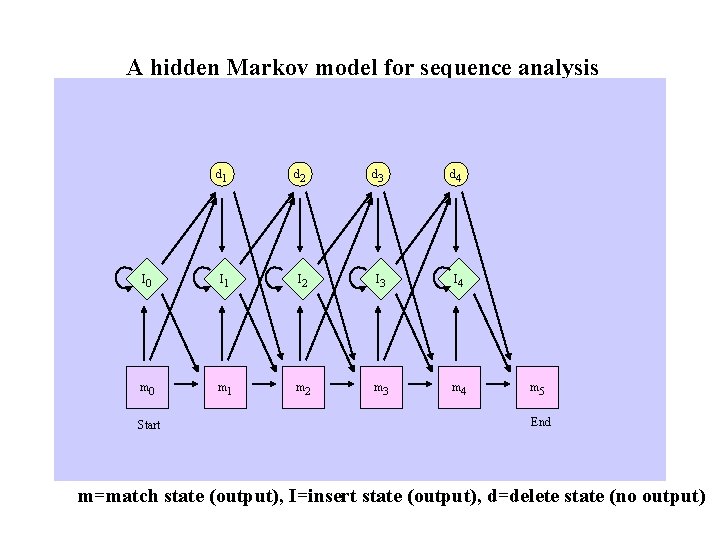
Hidden Markov Models HMMs) (� S = States {s 0, s 1, …. . , sn} V = Output alphabet {v 0, v 1, …. . , vm} A = { aij} = transition probability from si sj B = {bi(j)} = probability outputting vj in state si • What is the probability of a sequence of observations? • What are the maximum likelihood estimates of parameters in an HMM? • What is the most likely sequence of states that produced a given sequence of observations?

A hidden Markov model for sequence analysis d 1 d 2 d 3 d 4 I 0 I 1 I 2 I 3 I 4 m 0 m 1 m 2 m 3 m 4 Start m 5 End m=match state (output), I=insert state (output), d=delete state (no output)

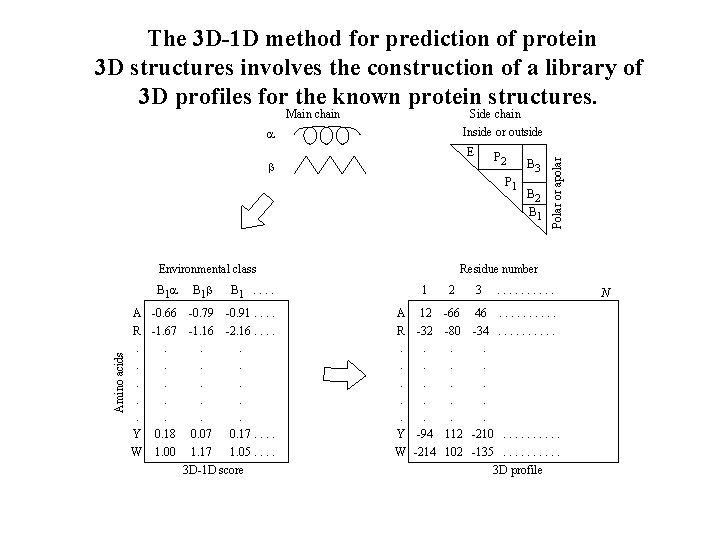
Prediction of protein 3 D structures Knowledge based prediction of protein 3 D or 3º structure can be classified into two categories: comparative modelling and fold recognition. The first can work well when there is significant sequence similarity to a protein with known 3 D structure. By contrast, fold recognition is used when no significant sequence similarity exists, and makes use of the knowledge and analysis of all protein structures. One such method due to Eisenberg and colleagues, involves 3 D-1 D alignment. Another such is threading.

The 3 D-1 D method for prediction of protein 3 D structures involves the construction of a library of 3 D profiles for the known protein structures. Side chain Inside or outside E P 2 b P 1 Environmental class Amino acids B 1 A -0. 66 R -1. 67. . Y 0. 18 W 1. 00 B 1 b B 1. . -0. 79 -0. 91. . -1. 16 -2. 16. . . 0. 07 0. 17. . 1. 17 1. 05. . 3 D-1 D score B 3 B 2 B 1 Polar or apolar Main chain Residue number 1 A 12 R -32. . Y -94 W -214 2 3 . . -66 46. . -80 -34. . . . . 112 -210. . 102 -135. . 3 D profile N

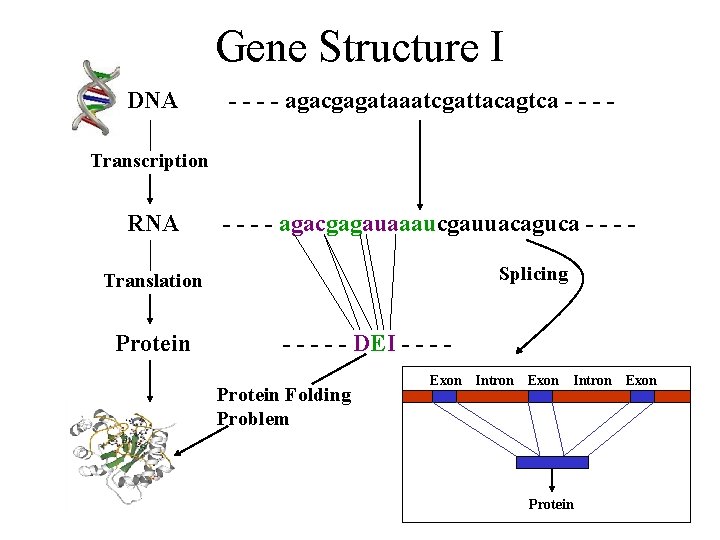
Gene Structure I DNA - - agacgagataaatcgattacagtca - - Transcription RNA - - agacgagauaaaucgauuacaguca - - - Splicing Translation Protein - - - DEI - - - Protein Folding Problem Exon Intron Protein Exon

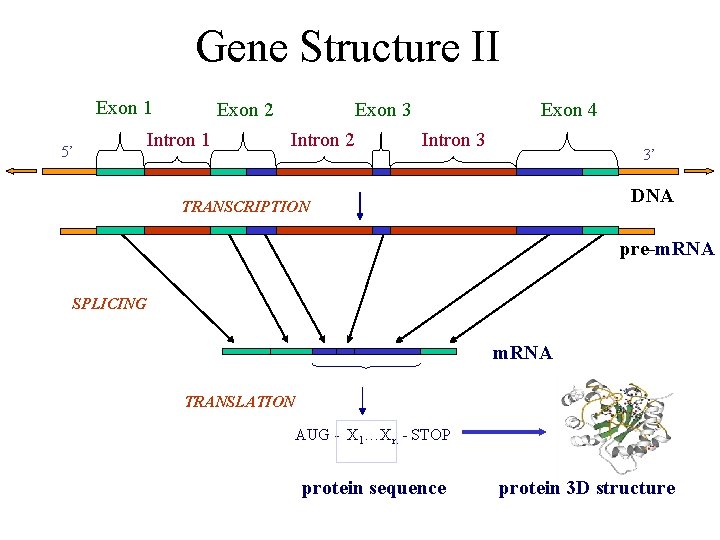
Gene Structure II Exon 1 5’ Exon 2 Intron 1 Exon 3 Intron 2 Exon 4 Intron 3 3’ DNA TRANSCRIPTION pre-m. RNA SPLICING m. RNA TRANSLATION AUG - X 1…Xn - STOP protein sequence protein 3 D structure

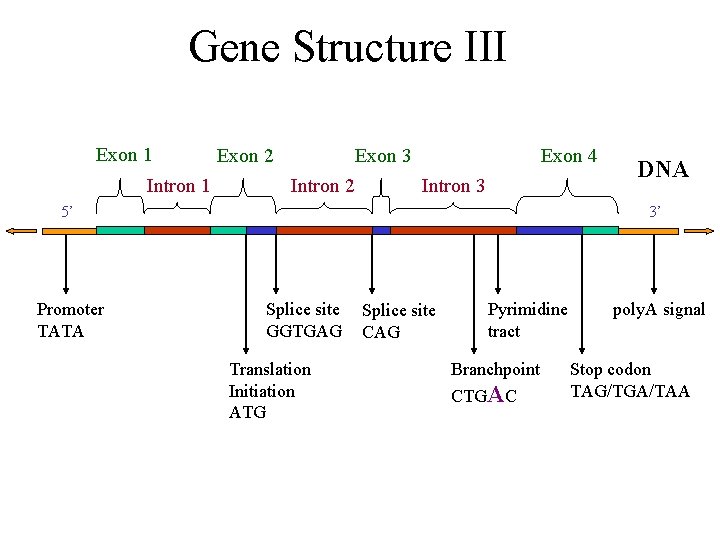
Gene Structure III Exon 1 Intron 1 Exon 2 Exon 3 Intron 2 Exon 4 Intron 3 5’ Promoter TATA DNA 3’ Splice site GGTGAG Translation Initiation ATG Splice site CAG Pyrimidine tract Branchpoint CTGAC poly. A signal Stop codon TAG/TGA/TAA

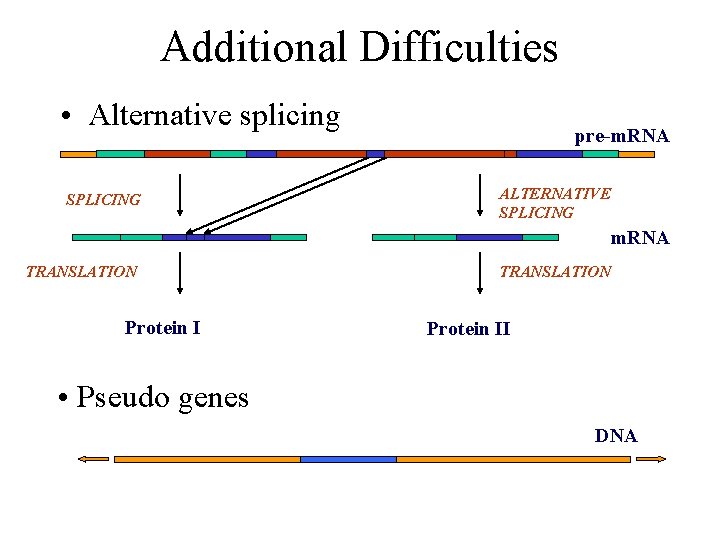
Additional Difficulties • Alternative splicing SPLICING pre-m. RNA ALTERNATIVE SPLICING m. RNA TRANSLATION Protein II • Pseudo genes DNA

Approaches to Gene Recognition • Homology BLASTN, TBLASTX, Procrustes • Statistical de novo GRAIL, FGENEH, Genscan, Genie, Glimmer • Hybrid Genome. Scan, Genie F(*, *, *, …)

Example: Glimmer Gene Finding in Microbial DNA • • No introns 90% coding Shorter genomes (less than 10 million bp) Lots of data

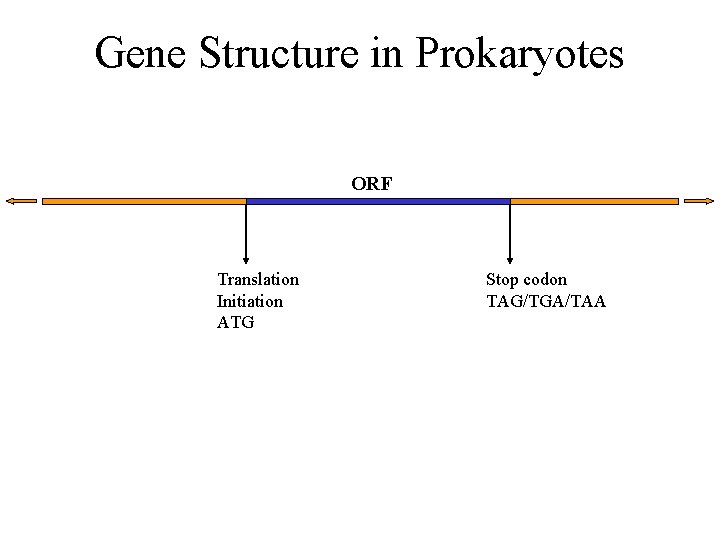
Gene Structure in Prokaryotes ORF Translation Initiation ATG Stop codon TAG/TGA/TAA

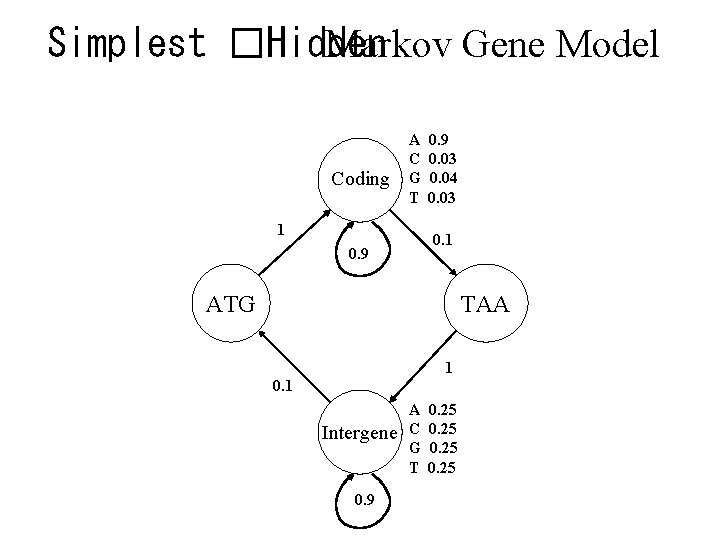
Simplest �Hidden Markov Gene Model Coding A C G T 1 0. 9 0. 03 0. 04 0. 03 0. 1 0. 9 ATG TAA 1 0. 1 Intergene 0. 9 A C G T 0. 25

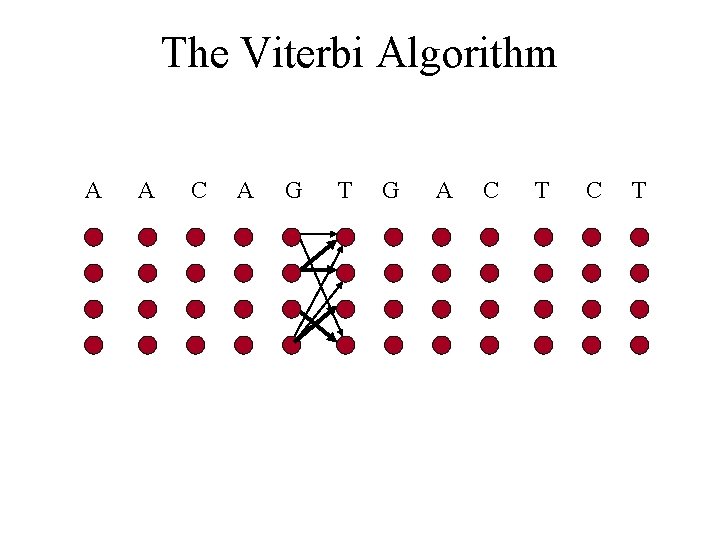
The Viterbi Algorithm A A C A G T G A C T

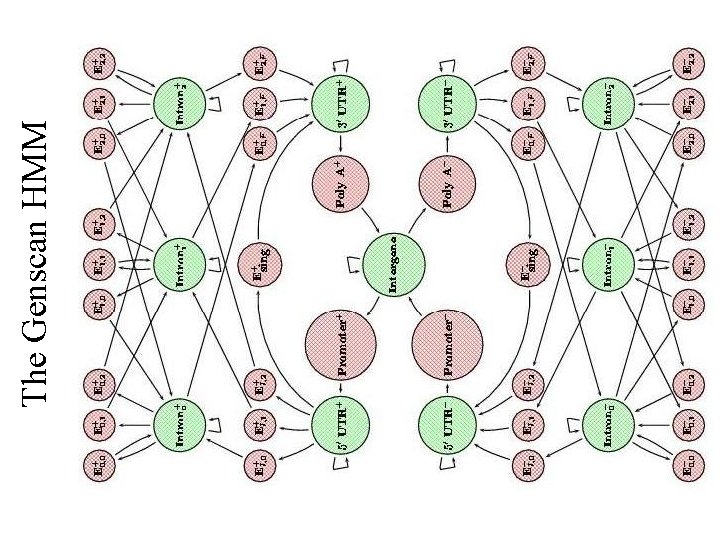
Example: Genscan Gene Finding in Human DNA • • Introns 5% coding Large genome (3 billion bp) Alternative splicing

The Genscan HMM

Examples of functional sites.

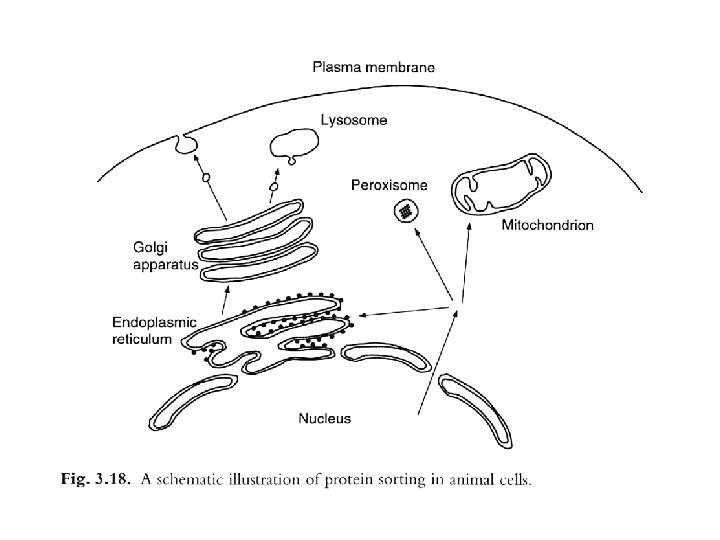
Protein sorting prediction The final step in informational expression of proteins involves their sorting to the appropriate location within or outside the cell. The information for correct localization is usually located within the protein itself.

Sequence Alignment Problem • Task: find common patterns shared by multiple Protein sequences • Importance: understanding function and structures; revealing evolutionary relationship, data organizing … • Types: Pairwise vs. Multiple; Global vs. Local. • Approaches: criteria-based (extension of pairwise methods) versus model-based (EM, Gibbs, HMM)

Outline of Liu-Lawrence approach • Local alignment --- Examples, the Gibbs sampling algorithm • A simple multinomial model for block-motifs and the Bayesian missing-data formulation. Possible but not covered here: • Motif sampler: repeated motifs. • The hidden Markov model (its decoupling) • The propagation model and beyond

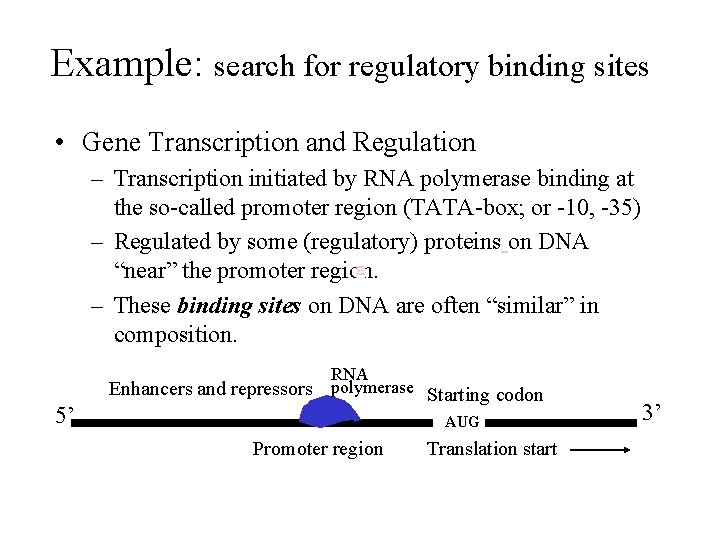
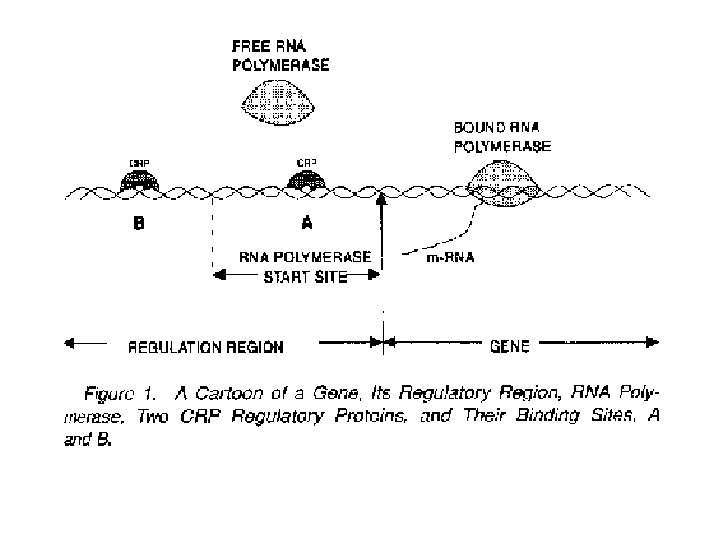
Example: search for regulatory binding sites • Gene Transcription and Regulation – Transcription initiated by RNA polymerase binding at the so-called promoter region (TATA-box; or -10, -35) – Regulated by some (regulatory) proteins on DNA “near” the promoter region. – These binding sites on DNA are often “similar” in composition. RNA 5’ Enhancers and repressors polymerase Starting codon AUG Promoter region Translation start 3’

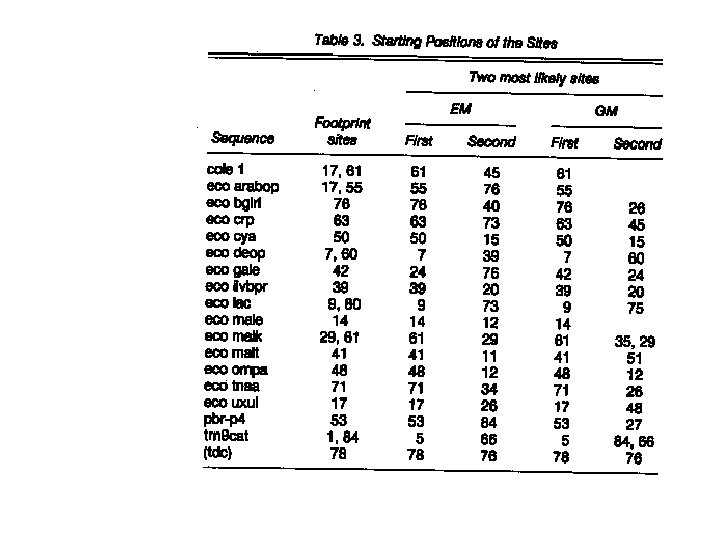
The particular dataset • 18 DNA segments, each of length 105 bps. • There at least one CRP binding sites, known experimentally, in each sequence. • The binding sites are about 16 -19 base pairs long, with considerable variability in their contents. • Interested in seeing if we can find these sites computationally.

The Data Set

Truth?

Example: H-T-H proteins u u u HTH: sequence-specific DNA binding, gene regulation. Motifs occur as local isolated structures. The whole 3 -D structures are known and very different. 30 sequences with known HTH positions chosen. The set represents a typically diverse cross section of HTH seq. Width of the motif pattern is assumed to be in the range from 17 to 22. The criterion “information per parameter” is used to determine the optimal width, 21. Heuristic convergence developed (multiple restarts with IPP monitored) Finding

Local Alignment of Multiple Sequences a 1 Local Motif a 2 width = w ak Alignment variable: A={a 1, a 2, …, ak} Objective: find the “best” common patterns. length nk

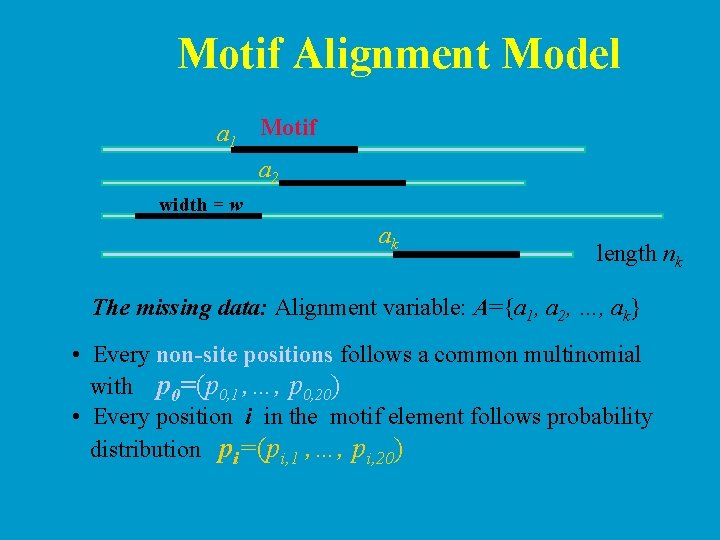
Motif Alignment Model a 1 Motif a 2 width = w ak length nk The missing data: Alignment variable: A={a 1, a 2, …, ak} • Every non-site positions follows a common multinomial with p 0=(p 0, 1 , …, p 0, 20) • Every position i in the motif element follows probability distribution pi=(pi, 1 , …, pi, 20)

The Tricky Part: The alignment variable A={a 1, a 2, …, ak} is not observable • General Missing Data problem: – Unobserved data in each datum – Object of the DP optimization (path) – Potentially observable – Examples • Alignment • RNA structure • Protein secondary structure

Statistical Models • How do we describe patterns? – frequencies of amino acid types. – multinomial distribution --- more generally a “model” A typical aligned motif

Multinomial Distribution A total of k sequences Model Mi for i-th column: (ki, 1, ki, 2, …, ki, 20) ~ Multinom (k, pi ) where pi=(pi, 1 , …, pi, 20)

Estimation for the “pattern” • The maximum likelihood: • Bayesian estimate: – Prior: pi ~ Dirichlet ( i, 1, . . . , i, 20), “pseudo-counts” – Posterior: [pi | obs ]~ Dirichlet ( i, 1, +ki, 1, …, i, 20 +ki, 20) – Posterior Mean: – Posterior Distribution:

Dealing with the missing data • Let Q=(p 0 , p 1 , … , pw ), “parameter”, A={a 1, a 2, …, a. K} • Iterative sampling: P(Q | A, Data); P(A | Q, Data) v. Draw from [Q | A, Data], then draw from [A | Q, Data] • Predictive Updating: pretend that K-1 sequences have been aligned. We stochastically predict for the K-th sequence!! a 1 a 3 a 2 ak ?

The Algorithm • Initialized by choosing random starting positions • Iterate the following steps many times: – Randomly or systematically choose a sequence, say, sequence k, to exclude. – Carry out the predictive-updating step to update ak • Stop when not much change observed, or some criterion met.

The PU-Step a 1 a 2 a 3 ak ? 1. Compute predictive frequencies of each position i in motif cij= count of amino acid type j at position i. c 0 j = count of amino acid type j in all non-site positions. qij= (cij+bj)/(K-1+B), B=b 1+ · · ·+ b. K “pseudo-counts” 2. Sample from the predictive distriubtion of ak.

Phase-shift and Fragmentation • Sometimes get stuck in a local shift optimum : True motif locations ak ? • How to “escape” from this local optimum? – Simultaneous move: A ®A+d, A+d={a 1+d, … , a. K+d} – Use a Metropolis step: accept the move with prob=p, Compare entropies between new columns and left-out ones.

Acknowledgements for slides used PDB: protein figures Lior Pachter: gene finding Jun Liu: Gibbs sampler