Sequence Alignment Sequence Alignment AGGCTATCACCTGACCTCCAGGCCGATGCCC TAGCTATCACGACCGCGGTCGATTTGCCCGAC AGGCTATCACCTGACCTCCAGGCCGATGCCC TAGCTATCACGACCGCGGTCGATTTGCCCGAC

Sequence Alignment

Sequence Alignment AGGCTATCACCTGACCTCCAGGCCGATGCCC TAGCTATCACGACCGCGGTCGATTTGCCCGAC -AGGCTATCACCTGACCTCCAGGCCGA--TGCCC--|| ||||||| ||||| TAG-CTATCAC--GACCGC--GGTCGATTTGCCCGAC

Distance from sequences Mutation events Mutation we need a score for the substitution of the symbol i with j (amino acidic residues, nucleotides, etc. ) substitution matrices s(i, j) A: B: ALASVLIRLITRLYP ASAVHLNRLITRLYP The substitution matrix should account for the underlying biological process (conserved structures or functions)

Substitution matrices The basic idea is to measure the correlation between 2 sequences Given a pair of “correlated” sequences we measure the substitution frequency of a-> b ( assuming symmetry) Pab The null hypothesis (random correlation or independent events) is the product Pa. Pb We then define s (a, b) = log(Pab/Pa. Pb) (log is additive so that the probability => sum over pairs) Minimal distance = Maximum score (s)

Substitution matrices Following this idea several matrices have been derived Their main difference is relative to the alignment types used for computing the frequencies PAMx: (Point Accepted Mutation). Number x % of mutation events. The matrix is built as: A 1 ik = P(k|i) for sequences with 1% mutations. Anik=(A 1 ik)n n % mutation events (number of mutations NOT mutated residues. E. g. : n=2 P(i|k) = Sa P(i|a) P(a|k) PAMn = Log(Anij /Pi)

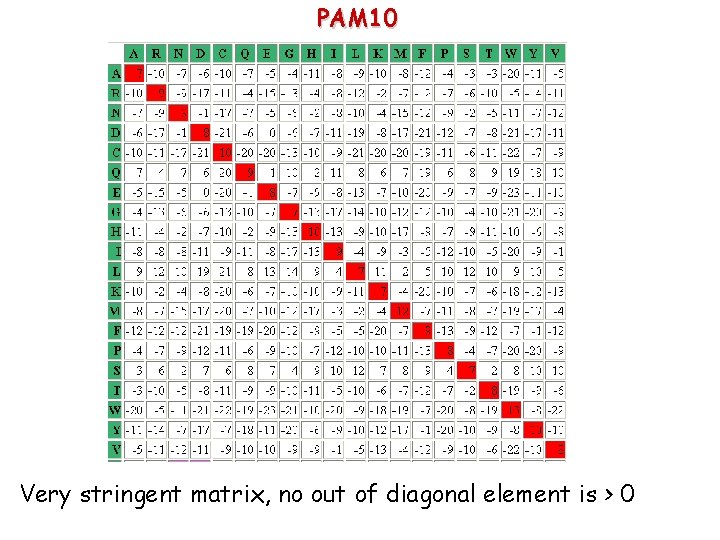
PAM 10 Very stringent matrix, no out of diagonal element is > 0

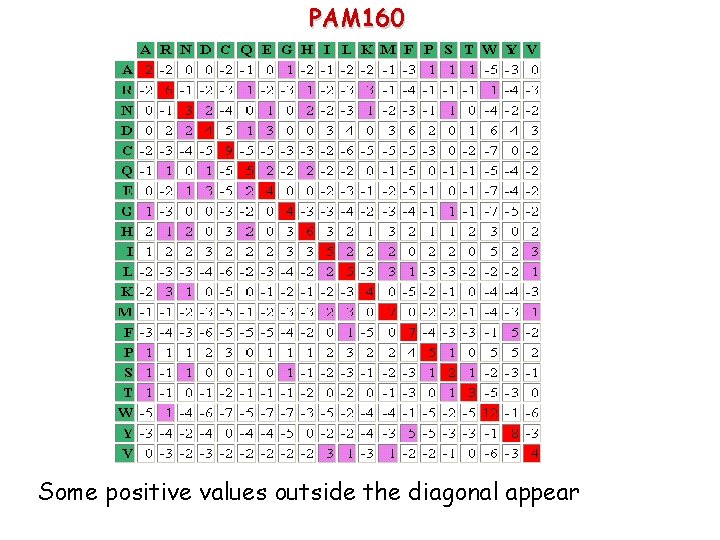
PAM 160 Some positive values outside the diagonal appear

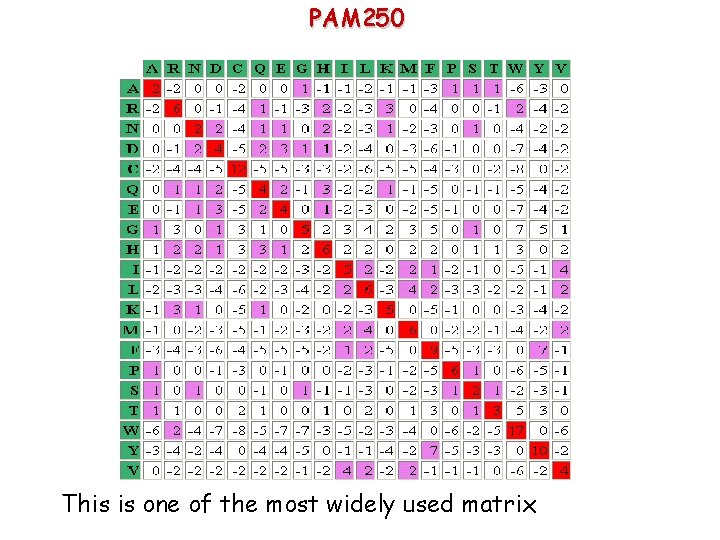
PAM 250 This is one of the most widely used matrix

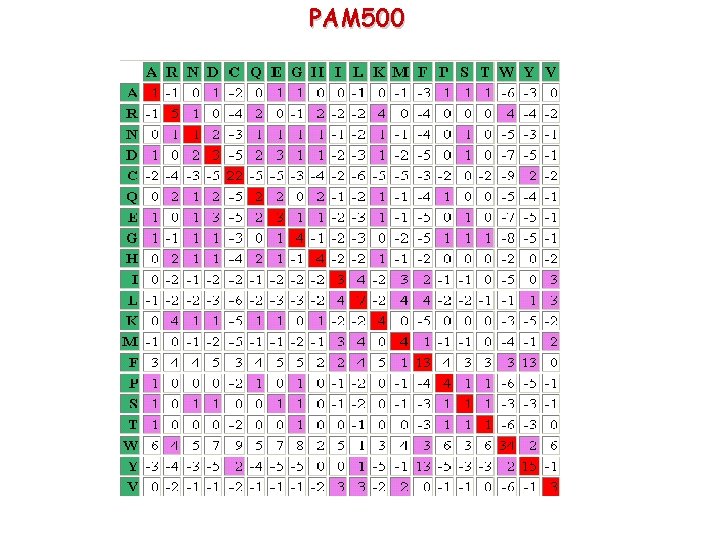
PAM 500

Substitution matrices PAM matrices are computed starting from very similar sequences and more distance scoring matrices are derived by matrix products BLOSUMx: This family is computed directly from blocks of alignments with a defined sequence identity threshold (> x%). => For very related sequences we must use PAM with low numbers and BLOSUM with large numbers. The opposite holds for distant sequences

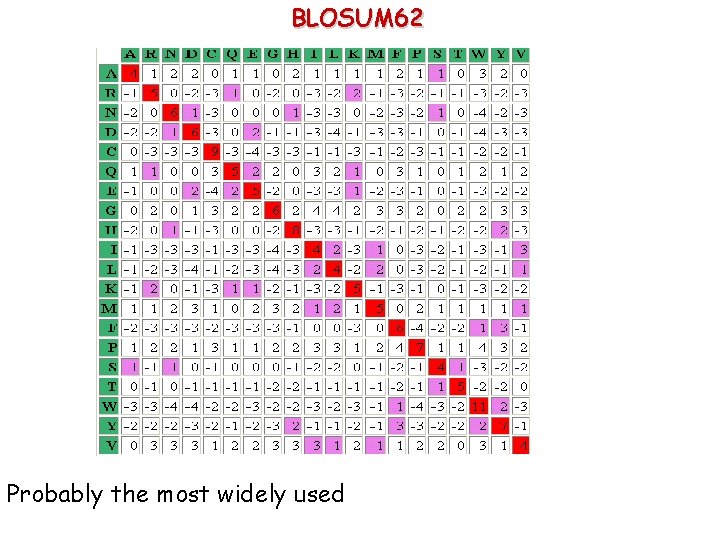
BLOSUM 62 Probably the most widely used

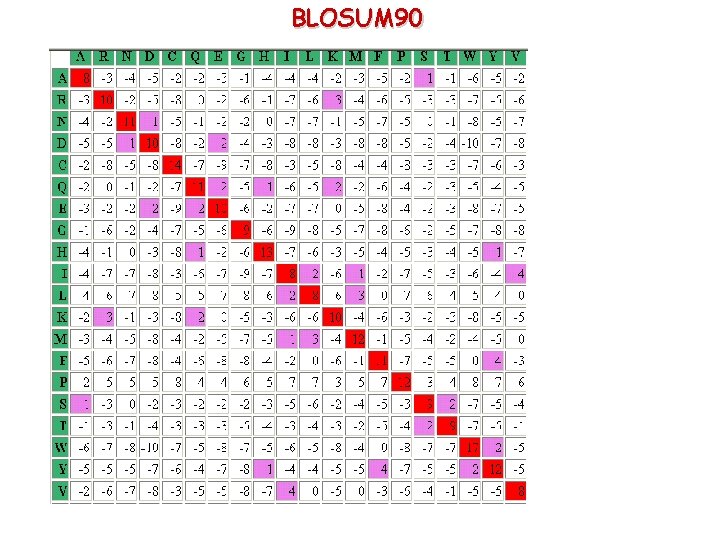
BLOSUM 90

BLOSUM 30

Exercise: Write your own substitution Matrix: Given e set of aligned sequences compute the Pab=frequency of mutations between a->b (assume symmetry, a->b counts also as b->a). Pa=as the marginal probability of Pab Finally, derive the substitution matrix: s (a, b) = log(Pab/Pa. Pb) Use the files provided at: http: //www. biocomp. unibo. it/piero/ICSA/Malignments/ Hints: 1. start with toy. aln to check your algorithm 2. Initialize your P[a][b] matrix with pseudocounts (such as 1 instead of 0)

Dot. Plots:

Dot. Plot Exercise: Write a program dotplot. py That takes as input a fasta file with two sequences A scoring matrix and sliding window, such as: dotplot. py fasta. in score. mat 11 and prints on the standard oputput the dotplot.

Distance between sequences What kind of operations we consider? Mutation Deletion and Insertion (rarely rearrangements ) A: B: ALASVLIRLIT--YP ASAVHL---ITRLYP The negative gap score value depends only on the number of holes (n) = -nd linear (n) = -d - (n-1)e affine (d: open e: extension) !! Please note that all scores are position-independent along the sequence

Pairwise alignment Given 2 sequences what is an alignment with a maximum score? Naïf solution: try every possible alignments and select one with the best score Using the score function :

How may alignments there are? Case without internal gaps --AAA BB--- -AAA BB-- AAA BB- AAA -BB AAA----BB Given 2 sequences of length m e n, the number of shifts is m +n +1

How may alignments there are? Case with internal gaps --AAA BB--BBAAA -AAA A-AA BB-B-BB--B BB-BABAA BAABA BAAAB ABBAA AAA BBABABA AAA B-B ABAAB AA-A -BBAABBA AAA -BB AABAB AAA--BB. . . AAABB The number of the alignments is equal at the number of all possible way of mixing 2 sequences keeping track of the original sequence order. Given 2 sequences of lengths n and m, they are ∑k=0, min(m, n)(m+n-k)!/k!(n-k)!(m-k)! For n=m=80 we get > 1043 possible alignments !!!!!!!

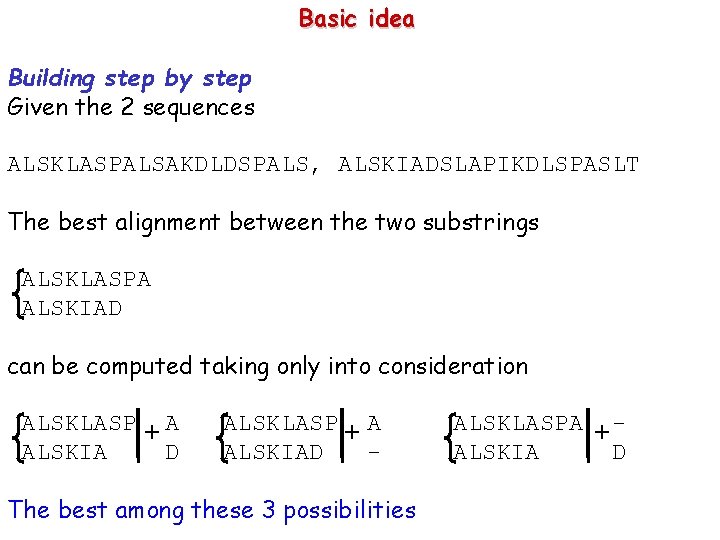
Basic idea We can keep a table of the precomputed substring alignments (dynamic programming) ALSKLASPALSAKDLDSPALS ALSKIADSLAPIKDLSPASLT ALSKLASPALSAKDLDSPAL-S ALSKIADSLAPIKDLSPASLTALSKLASPALSAKDLDSPALSALSKIADSLAPIKDLSPASL-T

Basic idea Building step by step Given the 2 sequences ALSKLASPALSAKDLDSPALS, ALSKIADSLAPIKDLSPASLT The best alignment between the two substrings ALSKLASPA ALSKIAD can be computed taking only into consideration ALSKLASP + A ALSKIA D ALSKLASP + A ALSKIAD - The best among these 3 possibilities ALSKLASPA + ALSKIA D

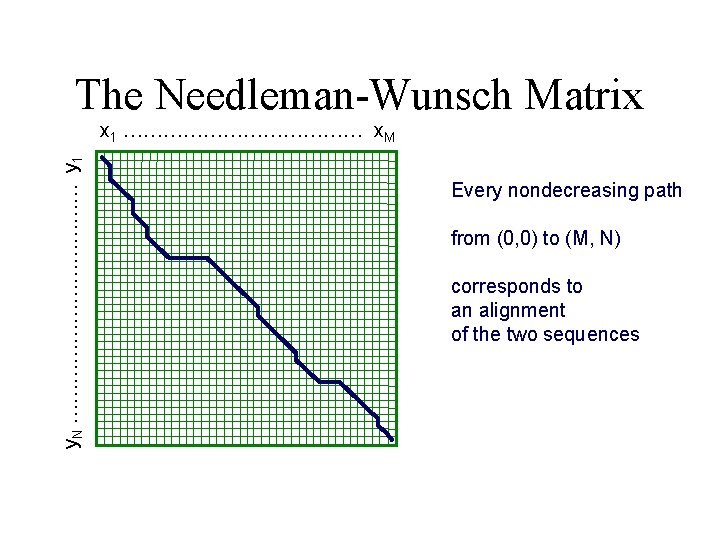
The Needleman-Wunsch Matrix y. N ……………… y 1 x 1 ……………… x. M Every nondecreasing path from (0, 0) to (M, N) corresponds to an alignment of the two sequences

The Needleman-Wunsch Algorithm m = 1 x = AGTA y = ATA F(i, j) i = s = -1 d = -1 0 1 2 3 4 Optimal Alignment: j=0 1 2 3 F(4, 3) = 2 AGTA A - TA

The Needleman-Wunsch Algorithm Initialization. • • • F(0, 0) F(0, j) F(i, 0) = 0 =-j d =-i d Main Iteration. Filling-in partial alignments • For each i = 1……M For each j = 1……N F(i-1, j) – d [case 1] F(i, j) = max F(i, j-1) – d [case 2] F(i-1, j-1) + s(xi, yj) [case 3] UP, LEFT • if [case 1] Ptr(i, j) = if [case 2] DIAG if [case 3] Termination. F(M, N) is the optimal score, and from Ptr(M, N) can trace back optimal alignment

Exercise: Suppose you want only to know the score of a global alignment. => Write a program that given two input sequence (in a single file in fasta format), a gap cost and a similarity matrix computes the score of the global alignment in O(N*M) time and in O(M) space, where M and N are the lengths of the input sequences and M<=N

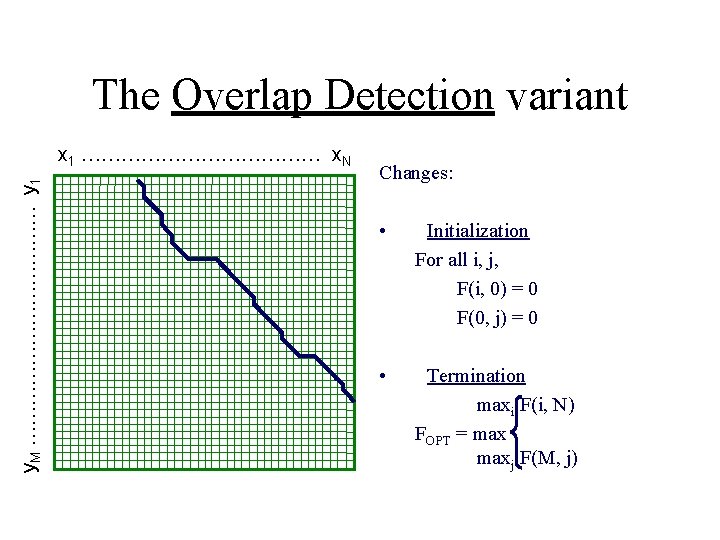
The Overlap Detection variant y. M ……………… y 1 x 1 ……………… x. N Changes: • Initialization For all i, j, F(i, 0) = 0 F(0, j) = 0 • Termination maxi F(i, N) FOPT = maxj F(M, j)

The local alignment problem Given two strings x = x 1……x. M, y = y 1……y. N Find substrings x’, y’ whose similarity (optimal global alignment value) is maximum e. g. x = aaaacccccgggg y = cccgggaacc

Why local alignment • Genes are shuffled between genomes • Portions of proteins (domains) are often conserved

The Smith-Waterman algorithm Idea: Ignore badly aligning regions Modifications to Needleman-Wunsch: Initialization: Iteration: F(0, j) = F(i, 0) = 0 F(i, j) = max 0 F(i – 1, j) – d F(i, j – 1) – d F(i – 1, j – 1) + s(xi, yj)

The Smith-Waterman algorithm Termination: • If we want the best local alignment… FOPT = maxi, j F(i, j) • If we want all local alignments scoring > t For all i, j find F(i, j) > t, and trace back

Scoring the gaps more accurately Current model: Gap of length incurs penalty n n d However, gaps usually occur in bunches Convex gap penalty function: G(n): for all n, G(n + 1) - G(n) - G(n – 1)

General gap dynamic programming Initialization: same Iteration: F(i, j) Termination: = max F(i-1, j-1) + s(xi, yj) maxk=0…i-1 F(k, j) – (i-k) maxk=0…j-1 F(i, k) – (j-k) same Running Time: O(N 2 M) Space: O(NM) (assume N>M)

Exercise: Write a program that given two input sequence (in a single file in fasta format), and a choice of a general gap function and scoring matrix computes the alignments of the two sequences and returns one of the possible best alignments. Remember that when you store that the best score is obtained using maxk=0…i-1 F(k, j) – g(i-k) maxk=0…j-1 F(i, k) – g(j-k) You have to store this information in the corresponding pointer (back-trace) matrix.

Compromise: affine gaps g(n) = d + (n – 1) e | | gap open extend To compute optimal alignment, At position i, j, need to “remember” best score if gap is open best score if gap is not open F(i, j): score of alignment x 1…xi to y 1…yj if xi aligns to yj G(i, j): score if xi, or yj, aligns to a gap

Needleman-Wunsch with affine gaps Initialization: F(0, 0)=0, F(i, 0) = d + (i – 1) e, F(0, j) = d + (j – 1) e R(0, j)= -∞ , C(i, 0)= -∞ Iteration: F(i, j) = max F(i – 1, j – 1) + s(xi, yj) R(i , j) C(i , j) F(i – 1, j) – d R(i, j) = max R(i – 1, j) – e F(i , j -1) – d C(i, j) = max C(i , j -1 ) – e Termination: same

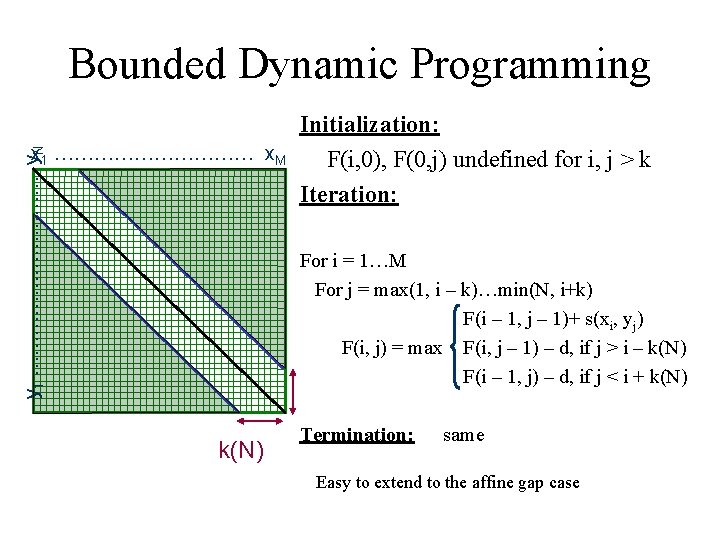
Bounded Dynamic Programming Assume we know that x and y are very similar Assumption: Then, # gaps(x, y) < k(N) xi | yj implies ( say N>M ) | i – j | < k(N) We can align x and y more efficiently: Time, Space: O(N k(N)) << O(N 2)

Bounded Dynamic Programming y 1 …………… y. N x 1 …………… x. M Initialization: F(i, 0), F(0, j) undefined for i, j > k Iteration: For i = 1…M For j = max(1, i – k)…min(N, i+k) F(i – 1, j – 1)+ s(xi, yj) F(i, j) = max F(i, j – 1) – d, if j > i – k(N) F(i – 1, j) – d, if j < i + k(N) Termination: same Easy to extend to the affine gap case

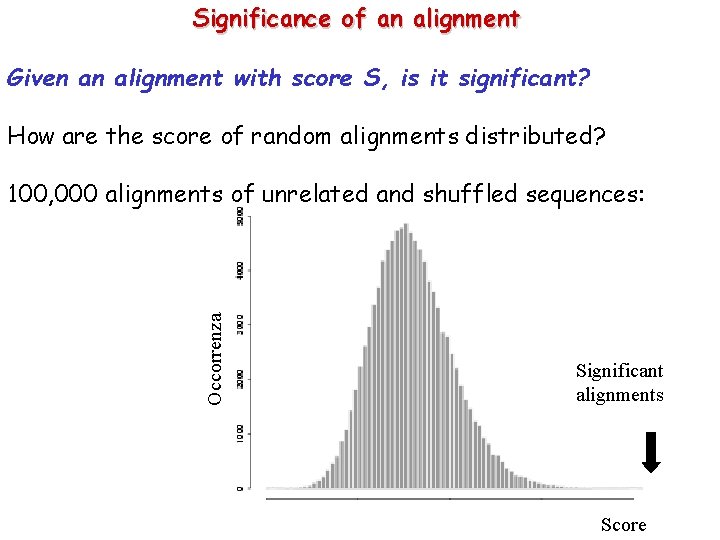
Significance of an alignment Given an alignment with score S, is it significant? How are the score of random alignments distributed? Occorrenza 100, 000 alignments of unrelated and shuffled sequences: Significant alignments Score

Z-score Z=(S-<S>)/ s S= Alignment score <S>= average of the scores on a random set of alignments s= Standard deviation of the scores on a random set of alignments Significance of the alignment Z<3 3<Z<10 Z>10 not significant probably significant

Execise: Z-score Write a program that takes in input a fasta with two sequences, and a number N. Compute the score of the global alignment of the two sequence and the Z-score with respect N shuffled sequences (generated from the first of the fasta) against the original second sequence of the fasta. Z=(S-<S>)/�s S= Alignment score <S>= average of the scores on a random set of alignments � s Standard deviation of the scores on a random set of alignments

Is the Z-score reliable? The Z-score of this alignment is 7. 5 over 54 residues Sequence identity is as high as 25. 9%. The sequences have a completely different structure Citrate synthase (2 cts) vs transthyritin (2 paba)

E-value Expected number of random alignments obtaining a score greater or equal to a given score (s) Relies on the Extreme Value Distribution E=Kmn e- s m, n: lengths of the sequences K, : “scaling” constants The number of high scoring random alignment increases when the sequence lengths increase and decreases in an exponential way when the score increases.

E-value Alignment significance The significance of the E-value depends on the length of the considered database. Considering Swiss Prot, E> 10 -1 > E > 10 -3 10 -3 > E > 10 -8 E < 10 -8 non significant probably not significant probably significant

P-value Probability for random alignments to obtain a score greater or equal to a given score (s) Given the E-value (expected number of alignments), which statistics do describe the probability of having a number a of random alignments with score ≥ S? Poisson: P(a) = Which is the probability of finding at least one random alignment with score ≥ S? P(a ≥ 1) = 1 – P(0) = 1 – exp (-E)

Similarity search in Data Bases Given a sequence, search for similar sequences in huge data sets In principle, the alignments between the query sequence and ALL the sequences in the data sets could be tried Too many sequences! Heuristic algorithms can be used. They do not assure to find the optimal alignment FASTA BLAST

FASTA The query sequence is chopped in words of k-tup characters. Usually k-tup = 2 for proteins, 6 for DNA ADKLPTLPLRLDPTNMVFGHLRI Words (indexed by position): AD, DK, KL, LP, PT, TL, LP, PR, RL, …, …, 1 2 3 4 5 6 7 8 9 …. The list of indexed words is compiled for each sequence in the data set (subject) The search of the correspondence between the words is very fast. The difference between the indexes of the matches in the query and the subject sequences determines the distance from the main diagonal

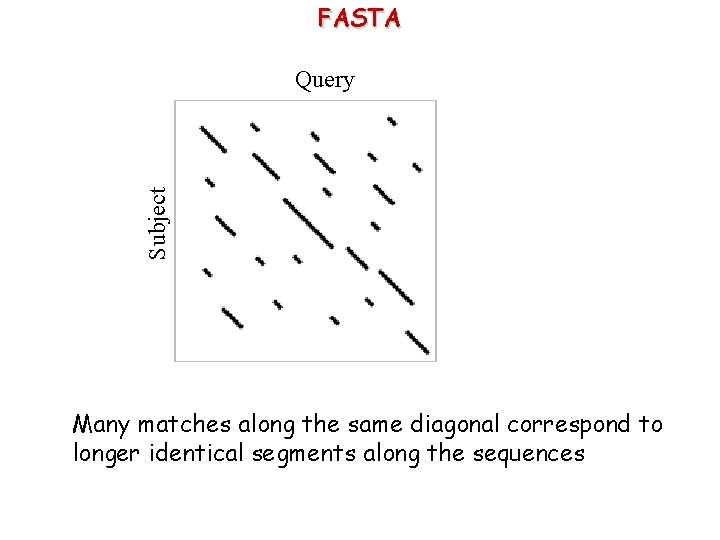
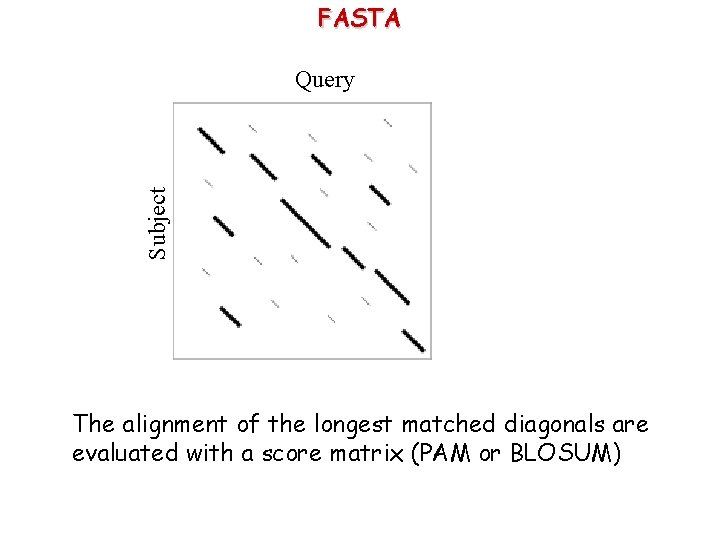
FASTA Subject Query Many matches along the same diagonal correspond to longer identical segments along the sequences

FASTA Subject Query The alignment of the longest matched diagonals are evaluated with a score matrix (PAM or BLOSUM)

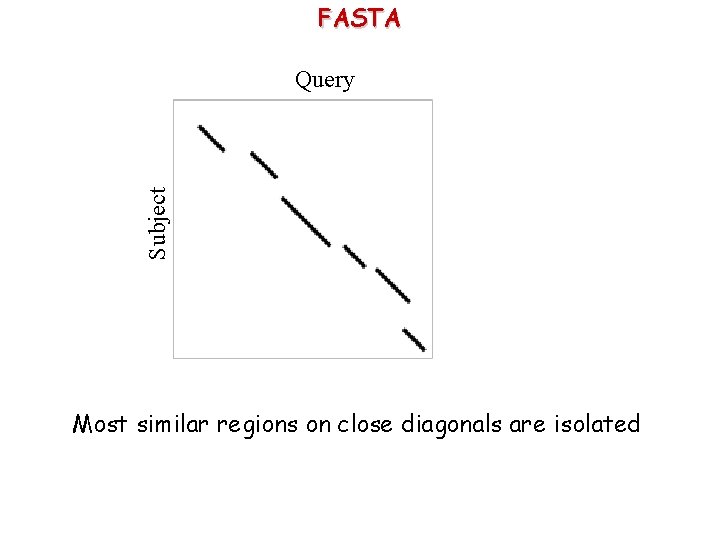
FASTA Subject Query Most similar regions on close diagonals are isolated

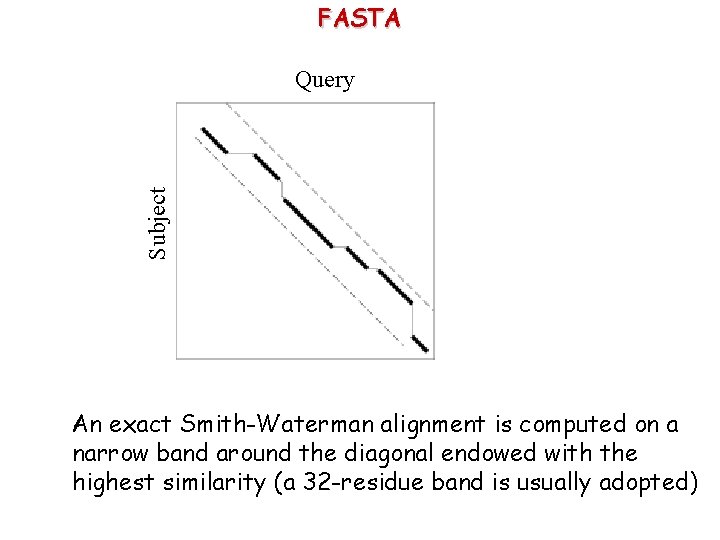
FASTA Subject Query An exact Smith-Waterman alignment is computed on a narrow band around the diagonal endowed with the highest similarity (a 32 -residue band is usually adopted)

Sequence similarity with FASTA

BLAST The sequence data set is indexed as follow: for each possible residue triplet the occurrence and the position along the sequences are stored. (FORMATDB) AAA AAC AAD ACA. .

BLAST The query sequence is chopped in words, W-residue long (usually W=3 for proteins) LSHLPTLPLRLDPTNMVFGHLRI LSH, SHL, HLP, LPT, PTL, TLR, …, …, For each word, all the similar proteins are generated, using the BLOSUM 62 matrix and setting a similarity threshold (usually T = 11 --13) LSH ISH MSH VSH LAH LTH LNH 16 14 14 13 13

BLAST Each word included in the list of the similar words is retrieved in the sequence of the data set by means of the indexes The match is extended, until the score is higher than a threshold S

Sequence similarity with BLAST (Basic Local Alignment Search Tool)

Alignment of all the retrieved sequences TTENTION: It is not a multiple sequence alignment

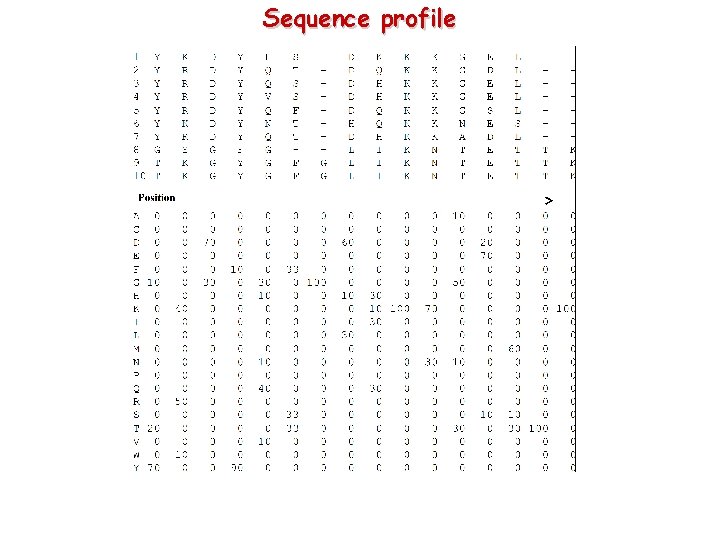
Sequence profile

Usefulness of the sequence profiles Sequence profiles describes the basic features of all the sequence used in the alignment Most conserved regions and most frequent mutations for each position are highlighted Sequence-to-profile alignment The alignment score are weighted position by position using the profile. The same mutations in different positions are scored with different values

Sequence-to-profile alignment Given the position i along a sequence profile, it is represented by a 20 -valued vector Pi = Pi(A) Pi(C) …… Pi (Y) Given the residue in position j along the sequence to align: Sj The score for aligning Sj to the vector Pi is: where M is a matrix score (BLOSUM or PAM)

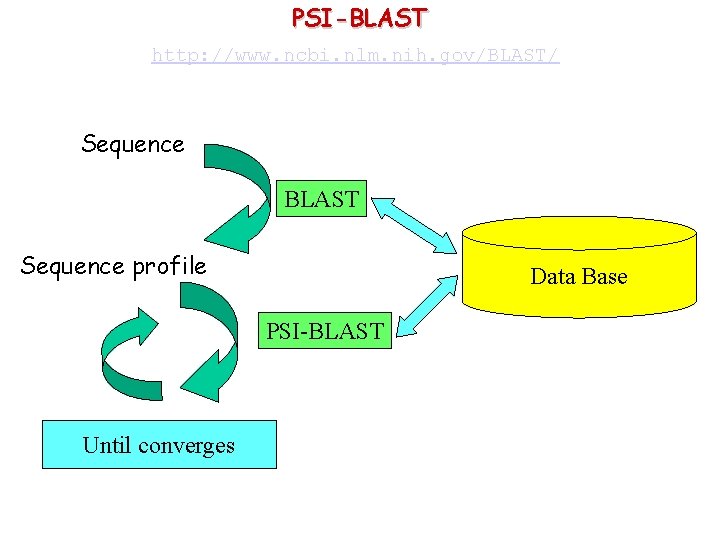
PSI-BLAST http: //www. ncbi. nlm. nih. gov/BLAST/ Sequence BLAST Sequence profile Data Base PSI-BLAST Until converges

The design of PSI-BLAST • • • PSI-BLAST takes as an input a single protein sequence and compares it to a protein database, using the gapped BLAST program The program constructs a multiple alignment, and then a profile, from any significant local alignments found. The original query sequence serves as a template for the multiple alignment and profile, whose lengths are identical to that of the query. Different numbers of sequences can be aligned in different template positions The profile is compared to the protein database, again seeking local alignments. After a few minor modifications, the BLAST algorithm can be used for this directly. PSI-BLAST estimates the statistical significance of the local alignments found. Because profile substitution scores are constructed to a fixed scale, and gap scores remain independent of position, the statistical theory and parameters for gapped BLAST alignments remain applicable to profile alignments. Finally, PSI-BLAST iterates, by returning to step (2), an arbitrary number of times or until convergence.