Sequence Alignment Evolution Evolution at the DNA level

Sequence Alignment

Evolution

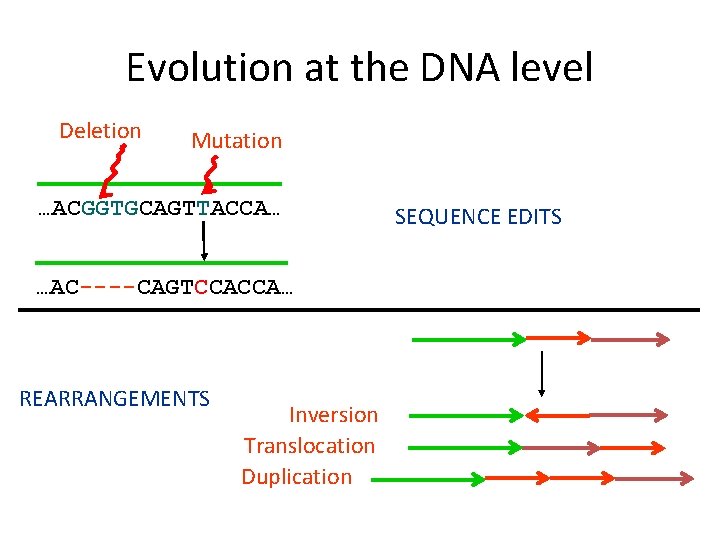
Evolution at the DNA level Deletion Mutation …ACGGTGCAGTTACCA… …AC----CAGTCCACCA… REARRANGEMENTS Inversion Translocation Duplication SEQUENCE EDITS

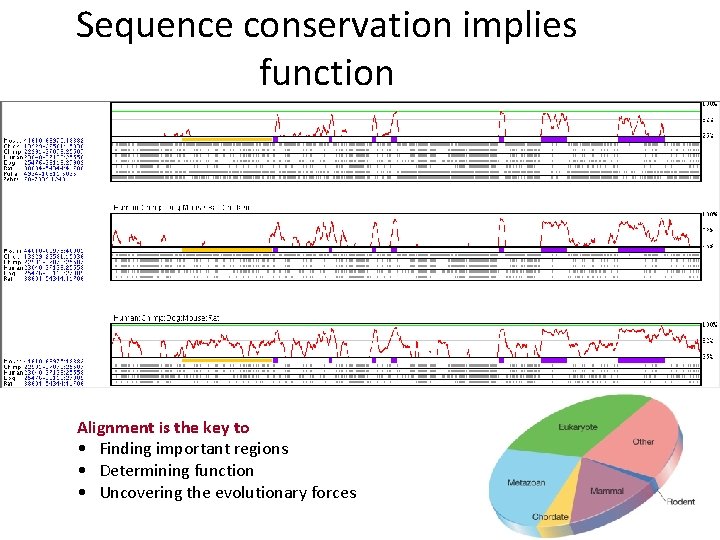
Sequence conservation implies function Alignment is the key to • Finding important regions • Determining function • Uncovering the evolutionary forces

Sequence Alignment AGGCTATCACCTGACCTCCAGGCCGATGCCC TAGCTATCACGACCGCGGTCGATTTGCCCGAC -AGGCTATCACCTGACCTCCAGGCCGA--TGCCC--TAG-CTATCAC--GACCGC--GGTCGATTTGCCCGAC Definition Given two strings x = x 1 x 2. . . x. M, y = y 1 y 2…y. N, an alignment is an assignment of gaps to positions 0, …, N in x, and 0, …, N in y, so as to line up each letter in one sequence with either a letter, or a gap in the other sequence

What is a good alignment? AGGCTAGTT, AGCGAAGTTT AGGCTAGTTAGCGAAGTTT 6 matches, 3 mismatches, 1 gap AGGCTA-GTTAG-CGAAGTTT 7 matches, 1 mismatch, 3 gaps AGGC-TA-GTTAG-CG-AAGTTT 7 matches, 0 mismatches, 5 gaps

Scoring Function • Sequence edits: AGGCCTC – Mutations AGGACTC. – Insertions AGGGCCTC – Deletions AGG. CTC Scoring Function: Match: +m Mismatch: -s Gap: -d Score F = (# matches) m - (# mismatches) s – (#gaps) d

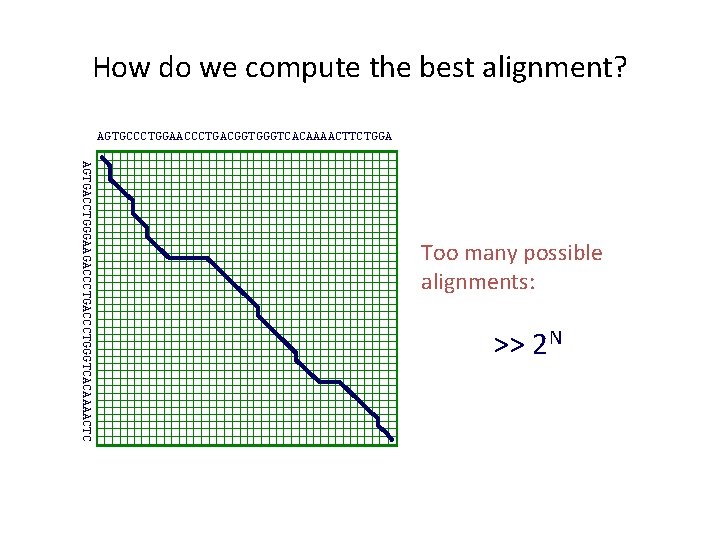
How do we compute the best alignment? AGTGCCCTGGAACCCTGACGGTGGGTCACAAAACTTCTGGA AGTGACCTGGGAAGACCCTGGGTCACAAAACTC Too many possible alignments: >> 2 N

Alignment is additive Observation: The score of aligning x 1……x. M y 1……y. N is additive Say that aligns to x 1…xi y 1…yj xi+1…x. M yj+1…y. N The two scores add up: F(x[1: M], y[1: N]) = F(x[1: i], y[1: j]) + F(x[i+1: M], y[j+1: N])

Dynamic Programming • There are only a polynomial number of subproblems – Align x 1…xi to y 1…yj • Original problem is one of the subproblems – Align x 1…x. M to y 1…y. N • Each subproblem is easily solved from smaller subproblems – ? ? ? • Then, we can apply Dynamic Programming!!! Let F(i, j) = optimal score of aligning x 1……xi y 1……yj

Dynamic Programming (cont’d) Notice three possible cases: 1. 2. 3. xi aligns to yj x 1……xi-1 xi y 1……yj-1 yj m, if xi = yj F(i, j) = F(i-1, j-1) + -s, if not xi aligns to a gap x 1……xi-1 xi y 1……yj - F(i, j) = F(i-1, j) - d yj aligns to a gap x 1……xi y 1……yj-1 yj F(i, j) = F(i, j-1) - d

Dynamic Programming (cont’d) How do we know which case is correct? Inductive assumption: F(i, j-1), F(i-1, j-1) are optimal Then, F(i, j) = max Where F(i-1, j-1) + s(xi, yj) F(i-1, j) – d F( i, j-1) – d s(xi, yj) = m, if xi = yj; -s, if not

Pairwise Sequence Alignment • As we’ve seen, sequence similarity is an indicator of homology • There are other uses for sequence similarity – Database queries – Comparative genomics –… 13

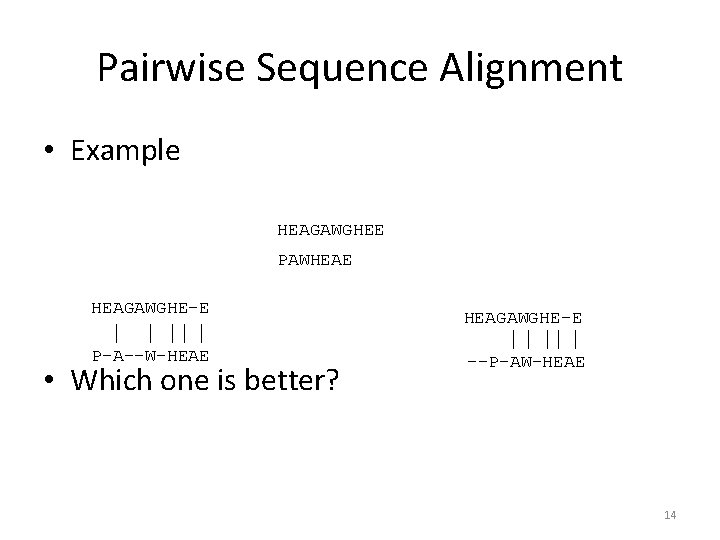
Pairwise Sequence Alignment • Example HEAGAWGHEE PAWHEAE HEAGAWGHE-E P-A--W-HEAE • Which one is better? HEAGAWGHE-E --P-AW-HEAE 14

Scoring • To compare two sequence alignments, calculate a score – PAM or BLOSUM matrices • Matches and mismatches – Gap penalty • Initiating a gap – Gap extension penalty • Extending a gap 15

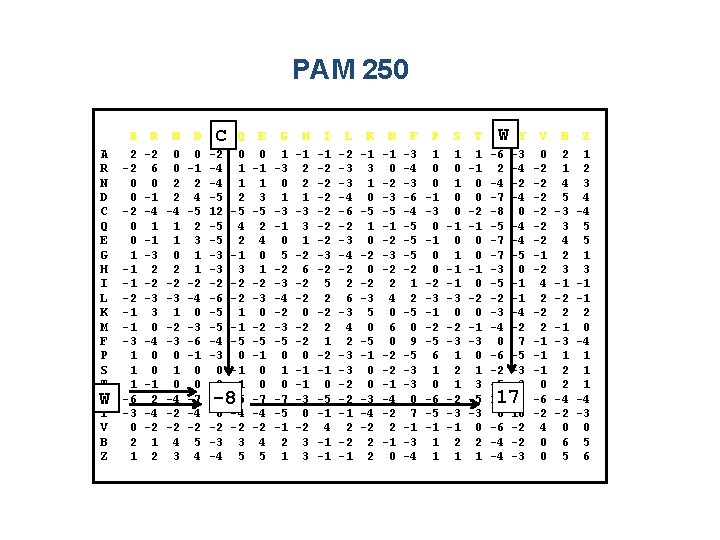
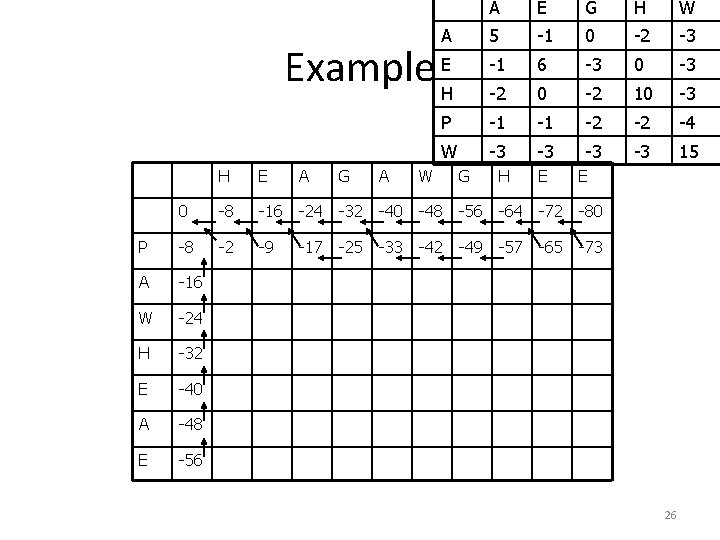
PAM 250 A R N D C Q E G H I L K M F P S T WW Y V B Z A 2 -2 0 0 1 -1 -1 -2 -1 -1 -3 1 1 1 -6 -3 0 2 1 R -2 6 0 -1 -4 1 -1 -3 2 -2 -3 3 0 -4 0 0 -1 2 -4 -2 1 2 N 0 0 2 2 -4 1 1 0 2 -2 -3 1 -2 -3 0 1 0 -4 -2 -2 4 3 D 0 -1 2 4 -5 2 3 1 1 -2 -4 0 -3 -6 -1 0 0 -7 -4 -2 5 4 C C -2 -4 -4 -5 12 -5 -5 -3 -3 -2 -6 -5 -5 -4 -3 0 -2 -8 0 -2 -3 -4 Q 0 1 1 2 -5 4 2 -1 3 -2 -2 1 -1 -5 0 -1 -1 -5 -4 -2 3 5 -8 E 0 -1 1 3 -5 2 4 0 1 -2 -3 0 -2 -5 -1 0 0 -7 -4 -2 4 5 G 1 -3 0 1 -3 -1 0 5 -2 -3 -4 -2 -3 -5 0 1 0 -7 -5 -1 2 1 H -1 2 2 1 -3 3 1 -2 6 -2 -2 0 -1 -1 -3 0 -2 3 3 I -1 -2 -2 -2 -3 -2 5 2 -2 2 1 -2 -1 0 -5 -1 4 -1 -1 L -2 -3 -3 -4 -6 -2 -3 -4 -2 2 6 -3 4 2 -3 -3 -2 -2 -1 K -1 3 1 0 -5 1 0 -2 -3 5 0 -5 -1 0 0 -3 -4 -2 2 2 M -1 0 -2 -3 -5 -1 -2 -3 -2 2 4 0 6 0 -2 -2 -1 -4 -2 2 -1 0 F -3 -4 -3 -6 -4 -5 -5 -5 -2 1 2 -5 0 9 -5 -3 -3 0 7 -1 -3 -4 P 1 0 0 -1 -3 0 -1 0 0 -2 -3 -1 -2 -5 6 1 0 -6 -5 -1 1 1 S 1 0 0 -1 0 1 -1 -1 -3 0 -2 -3 1 2 1 -2 -3 -1 2 1 T 1 -1 0 0 -2 -1 0 0 -1 0 -2 0 -1 -3 0 1 3 -5 -3 0 2 1 W Y W -6 -3 2 -4 -4 -2 -7 -4 -8 0 -5 -4 -7 -5 -3 0 -5 -1 -2 -1 -3 -4 -4 -2 0 7 -6 -5 -2 -3 -5 -3 17 0 0 10 -6 -2 -4 -3 17 V 0 -2 -2 -2 -1 -2 4 2 -2 2 -1 -1 -1 0 -6 -2 4 0 0 B 2 1 4 5 -3 3 4 2 3 -1 -2 2 -1 -3 1 2 2 -4 -2 0 6 5 Z 1 2 3 4 -4 5 5 1 3 -1 -1 2 0 -4 1 1 1 -4 -3 0 5 6

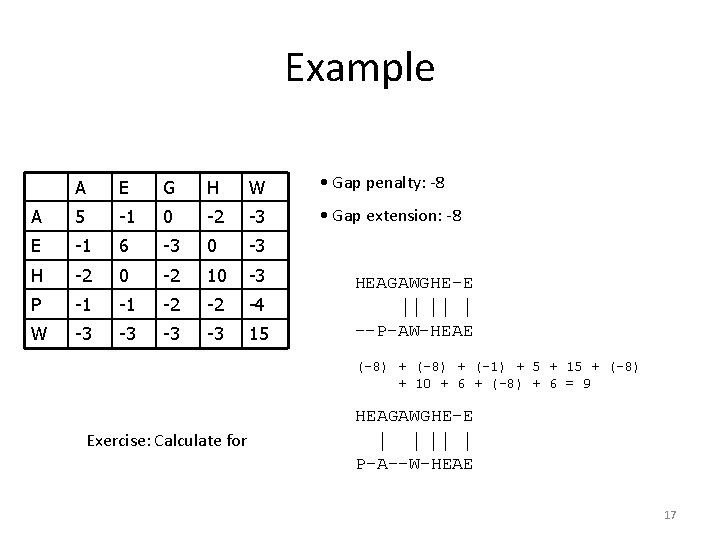
Example A E G H W • Gap penalty: -8 A 5 -1 0 -2 -3 • Gap extension: -8 E -1 6 -3 0 -3 H -2 0 -2 10 -3 P -1 -1 -2 -2 -4 W -3 -3 15 HEAGAWGHE-E --P-AW-HEAE (-8) + (-1) + 5 + 15 + (-8) + 10 + 6 + (-8) + 6 = 9 HEAGAWGHE-E Exercise: Calculate for P-A--W-HEAE 17

Formal Description • Problem: Pair. Seq. Align • Input: Two sequences x, y Scoring matrix s Gap penalty d Gap extension penalty e • Output: The optimal sequence alignment 18

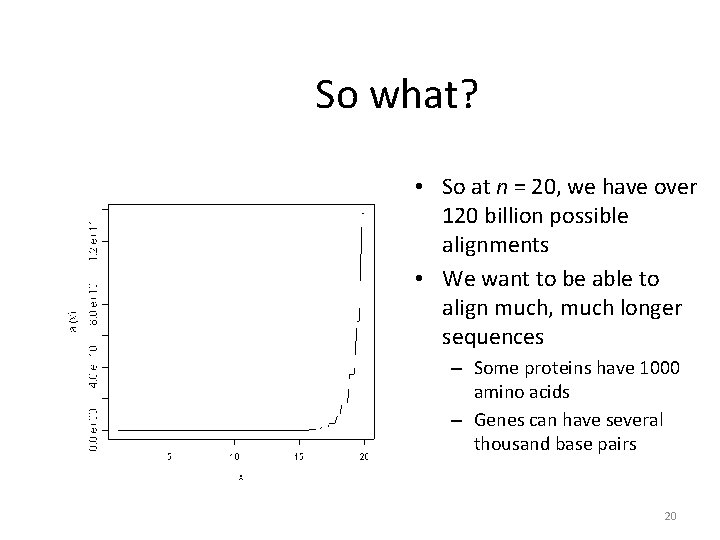
How Difficult Is This? • Consider two sequences of length n • There are possible global alignments, and we need to find an optimal one from amongst those! 19

So what? • So at n = 20, we have over 120 billion possible alignments • We want to be able to align much, much longer sequences – Some proteins have 1000 amino acids – Genes can have several thousand base pairs 20

Dynamic Programming • General algorithmic development technique • Reuses the results of previous computations – Store intermediate results in a table for reuse • Look up in table for earlier result to build from 21

Global Alignment • Needleman-Wunsch 1970 • Idea: Build up optimal alignment from optimal alignments of subsequences HEAG Add score from table --P-25 HEAG- HEAGA --P-A --P— --P-A -33 Gap with bottom -33 Gap with top -20 Top and bottom 22

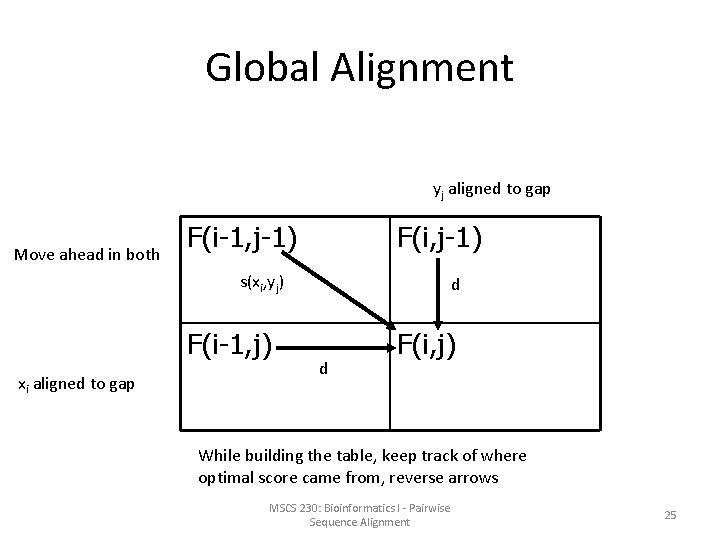
Global Alignment • Notation – xi – ith letter of string x – yj – jth letter of string y – x 1. . i – Prefix of x from letters 1 through I – F – matrix of optimal scores • F(i, j) represents optimal score lining up x 1. . i with y 1. . j – d – gap penalty – scoring matrix MSCS 230: Bioinformatics I - Pairwise Sequence Alignment 23

Global Alignment • The work is to build up F • Initialize: F(0, 0) = 0, F(i, 0) = id, F(0, j)=jd • Fill from top left to bottom right using the recursive relation MSCS 230: Bioinformatics I - Pairwise Sequence Alignment 24

Global Alignment yj aligned to gap Move ahead in both F(i-1, j-1) F(i, j-1) s(xi, yj) F(i-1, j) xi aligned to gap d d F(i, j) While building the table, keep track of where optimal score came from, reverse arrows MSCS 230: Bioinformatics I - Pairwise Sequence Alignment 25

A E G H W 5 -1 0 -2 -3 -1 6 -3 0 -3 -2 0 -2 10 -3 P -1 -1 -2 -2 -4 W -3 -3 15 A Example EH H E A G A W G H E E 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A -16 W -24 H -32 E -40 A -48 E -56 26

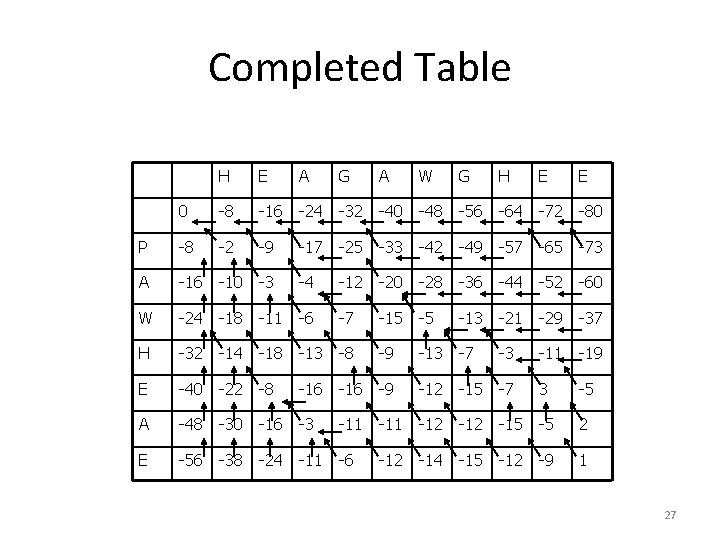
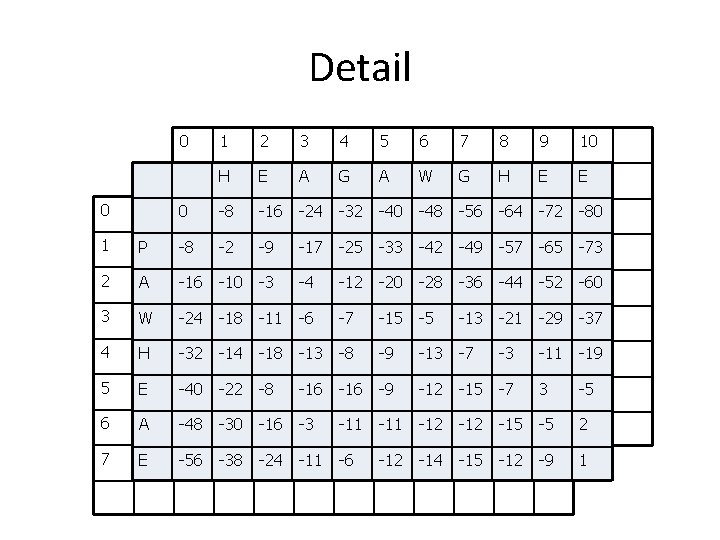
Completed Table H E A G A W G H E E 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A -16 -10 -3 -4 -12 -20 -28 -36 -44 -52 -60 W -24 -18 -11 -6 -7 -15 -5 -13 -21 -29 -37 H -32 -14 -18 -13 -8 -9 -13 -7 -3 -11 -19 E -40 -22 -8 -16 -9 -12 -15 -7 3 -5 A -48 -30 -16 -3 -11 -12 -15 -5 2 E -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1 27

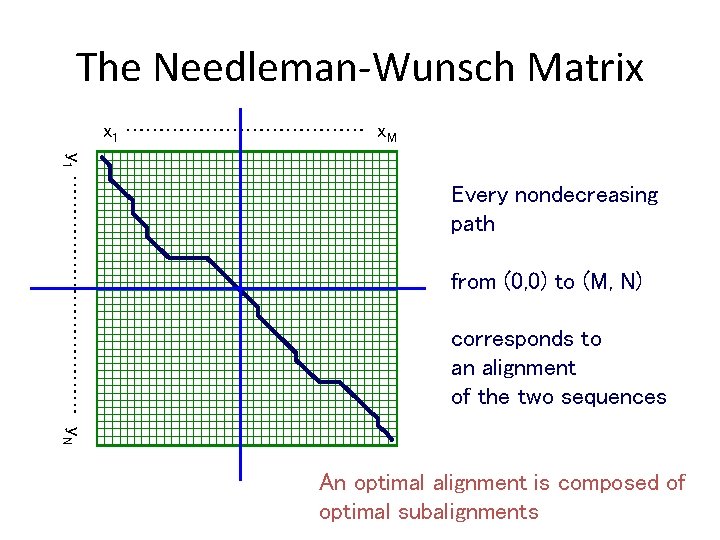
The Needleman-Wunsch Matrix x 1 ……………… x. M y 1 ……………… y. N Every nondecreasing path from (0, 0) to (M, N) corresponds to an alignment of the two sequences An optimal alignment is composed of optimal subalignments

Performance • Time: O(NM) • Space: O(NM)

Design a Perl Program • Is it doable by Perl? • How can we handle two-dimensional array?

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2

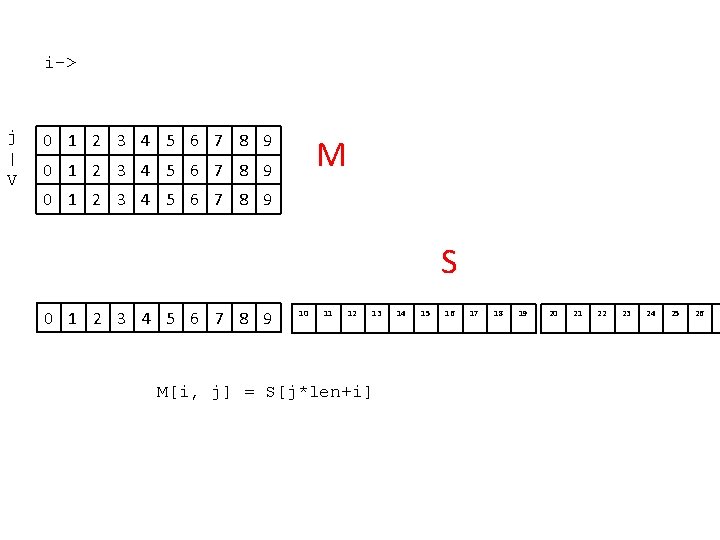
i-> j | V 0 1 2 3 4 5 6 7 8 9 M 0 1 2 3 4 5 6 7 8 9 S 0 1 2 3 4 5 6 7 8 9 10 11 12 13 M[i, j] = S[j*len+i] 14 15 16 17 18 19 20 21 22 23 24 25 26 2

Detail 0 1 2 3 4 5 6 7 8 9 10 H 0 E A G A W G H E E 4 -16 5 -24 6 -32 7 -40 8 -48 9 -56 10 -64 11 -72 -80 0 1 2 0 P 3 -8 1 P 0 -8 A -2 -16 -9 -17 -25 -33 -42 -49 -57 -65 -73 2 -8 A -16 W -10 -24 -3 -4 -12 -20 -28 -36 -44 -52 -60 3 -16 -24 W H -18 -32 -11 -6 -7 -15 -5 -13 -21 -29 -37 4 -24 -32 H E -14 -40 -18 -13 -8 -9 -13 -7 -3 -11 -19 5 E-32 -40 A -22 -48 -8 -16 -9 -12 -15 -7 3 -5 6 -40 -48 A E -30 -56 -16 -38 -3 -24 -11 -6 -12 -14 -15 -5 -12 2 -9 7 E-48 -56 -38 -14 -24 -11 -6 -12 -15 -12 -9 1