Separable Programming Pemrograman Terpisah Teknik Optimasi Semester Ganjil

Separable Programming (Pemrograman Terpisah) Teknik Optimasi Semester Ganjil 2013/2014

• Adalah masalah NLP dengan fungsi yang terdiri dari beberapa fungsi terpisah dan didekati dengan piecewise linear function • Dengan formulasi sbb:

Contoh • Fungsi obyektif dapat dipisahkan menjadi: • Fungsi kendala dapat dipisahkan menjadi:

• Pada separable programming daerah asal x 1 dan x 2 akan dibagi menjadi beberapa grid yang digunakan untuk mendekati fungsi tujuan dan kendala dengan piecewise linear function • aj dan bj (untuk j = 1, 2, …, n) sedemikian hingga nilai pada solusi optimal akan memenuhi aj ≤ xj ≤ bj • Berikutnya dipilih titik grid pj, 1 , pj, 2, …pj, k dengan aj = pj, 1 ≤ pj, 2 ≤ … ≤ pj, k = bj (untuk kesederhanaan, untuk setiap variabel dapat digunakan banyak grid yang sama ).

• Pada contoh dapat ditentukan bahwa • 0 ≤ x 1 ≤ 20 dan 0 ≤ x 2 ≤ 20 • Dan pembagian grid:
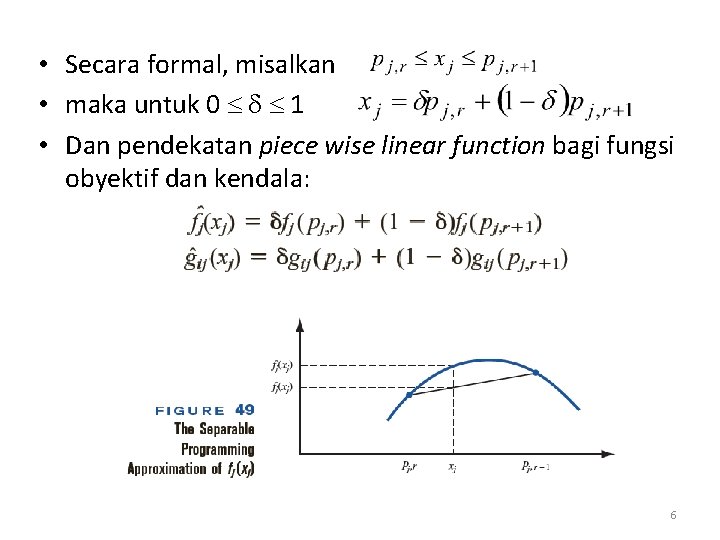
• Secara formal, misalkan • maka untuk 0 1 • Dan pendekatan piece wise linear function bagi fungsi obyektif dan kendala: 6

• Pada contoh: • Sehingga f 1(12) dapat didekati dengan:

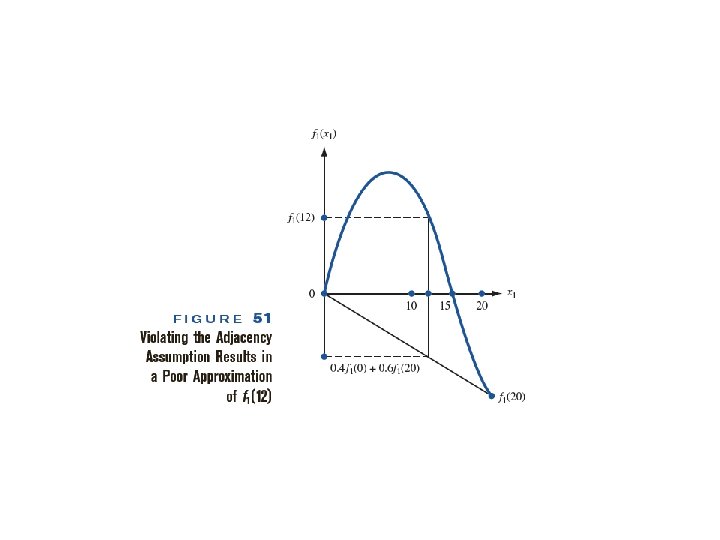
• Supaya pendekatan lebih akurat, kombinasi linier untuk peubah x harus menggunakan dua titik grid yang saling berdekatan (adjacency) • Misal: • Adalah pendekatan yang tidak tepat akibat grid yang digunakan saling berjauhan

• Secara umum, setiap peubah x dapat dinyatakan sebagai kombinasi linier dari setiap titik grid • Tambahan fungsi kendala yang menyatakan hal tsb dalam bentuk: • Hanya ada dua titik grid yang digunakan, dengan j, r >0 • Pemilihan titik grid juga harus saling berdekatan (adjacent) supaya pendekatan akurat

• Untuk j tertentu misalkan j, k positif maka j, k - 1 atau j, k+1 harus positif dan bukan j, r yang lain • j, k dikatakan adjacent dengan j, k - 1 dan j, k+1

Permasalahan Pendekatan bagi Pemrograman Terpisah • Adalah permasalahan pemrograman linier • Diselesaikan dengan metode simpleks dengan modifikasi untuk mempertahankan adjacency assumption

1. Jika untuk j tertentu, semua j, k = 0, maka setiap j, k boleh masuk sebagai basis. 2. Jika untuk j tertentu, j, k positif maka hanya j, k-1 atau j, k+1 yang boleh masuk sebagai basis 3. Jika untuk j tertentu, terdapat dua j, k yang positif, maka tidak boleh ada j, k lain yang dapat masuk sebagai basis
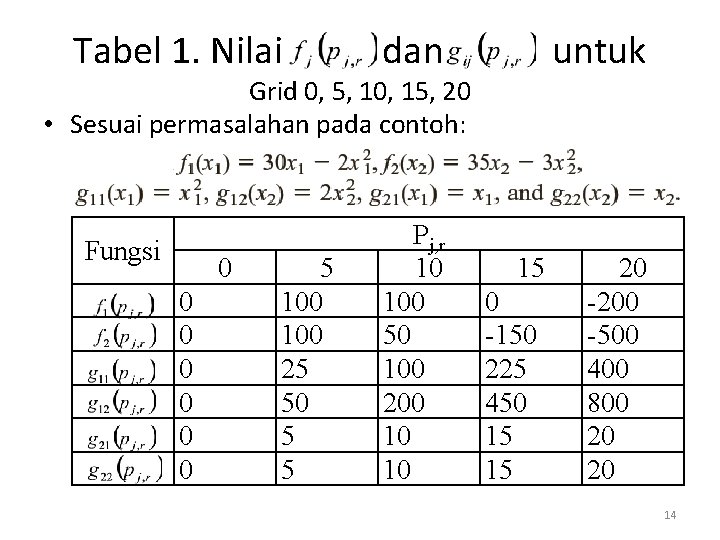
Tabel 1. Nilai dan untuk Grid 0, 5, 10, 15, 20 • Sesuai permasalahan pada contoh: Fungsi 0 0 0 0 5 100 25 50 5 5 Pj, r 10 100 50 100 200 10 10 15 0 -150 225 450 15 15 20 -200 -500 400 800 20 20 14

• Sehingga untuk contoh tsb, pendekatan linier yang digunakan: • Dan asumsi adjacency
- Slides: 15