Sensor Placement Estimation Force Based and Deflection Based

Sensor Placement Estimation Force Based and Deflection Based Models

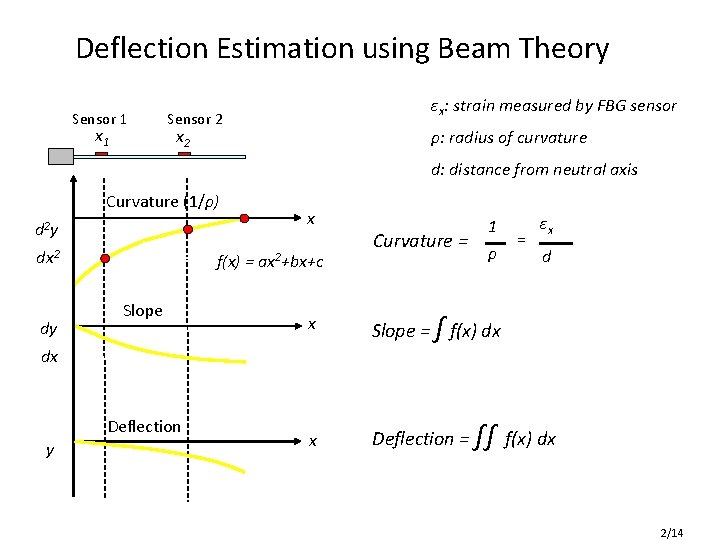
Deflection Estimation using Beam Theory Sensor 1 x 1 εx: strain measured by FBG sensor Sensor 2 x 2 ρ: radius of curvature d: distance from neutral axis Curvature (1/ρ) d 2 y dx 2 dy x f(x) = ax 2+bx+c Slope y ρ = εx d ∫ f(x) dx x Slope = x Deflection = dx Deflection Curvature = 1 ∫∫ f(x) dx 2/14

Force-Based Displacement • 2 locations of force concentration defined. • Moment of bending calculations determine curvature. • True deflection model calculated from curvature. • Estimate curvature determined from x 1, x 2, two sensor locations. • Estimated deflection = ∫∫curvature.

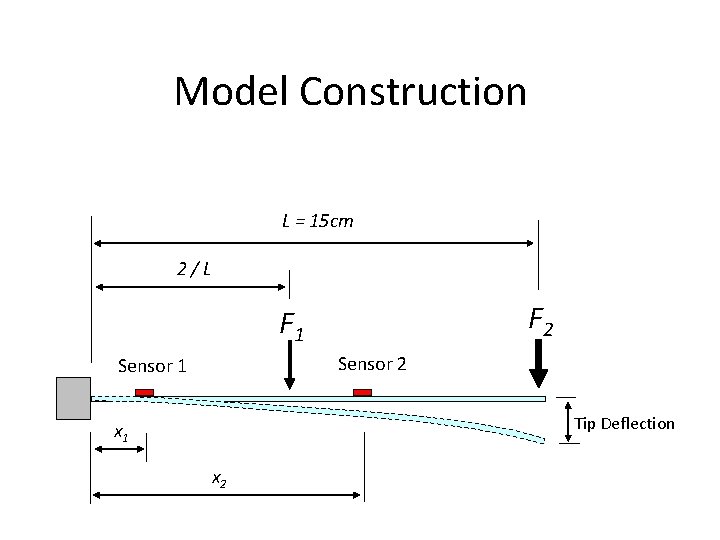
Model Construction L = 15 cm 2/L F 2 F 1 Sensor 2 Sensor 1 Tip Deflection x 1 x 2

Sensitivity • The sensitivity of the positions x 1 and x 2 where found as the deflection error at the tip of the needle with respect to x 1 and x 2.

Results: Force-Based Model • Magnitudes of forces had no effects on distribution of deflection error and sensitivities. • Whether the forces where applied in opposing directions also had no effect. • Only location of the applied forces changed the distribution of deflection error and sensitivities.

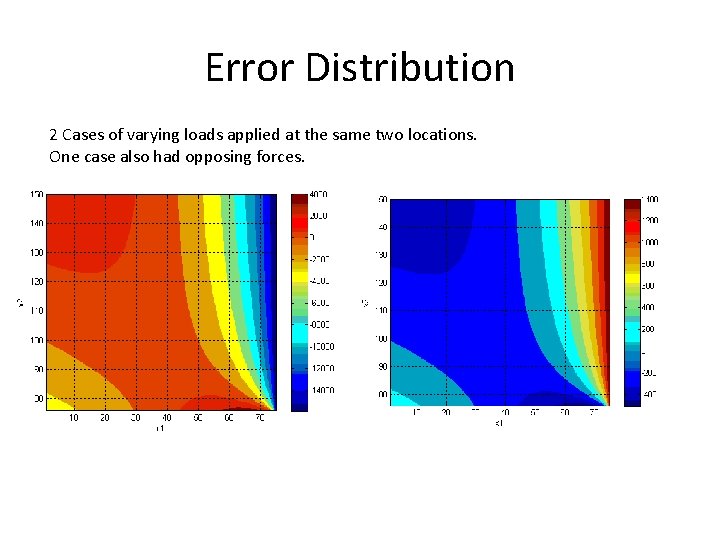
Error Distribution 2 Cases of varying loads applied at the same two locations. One case also had opposing forces.

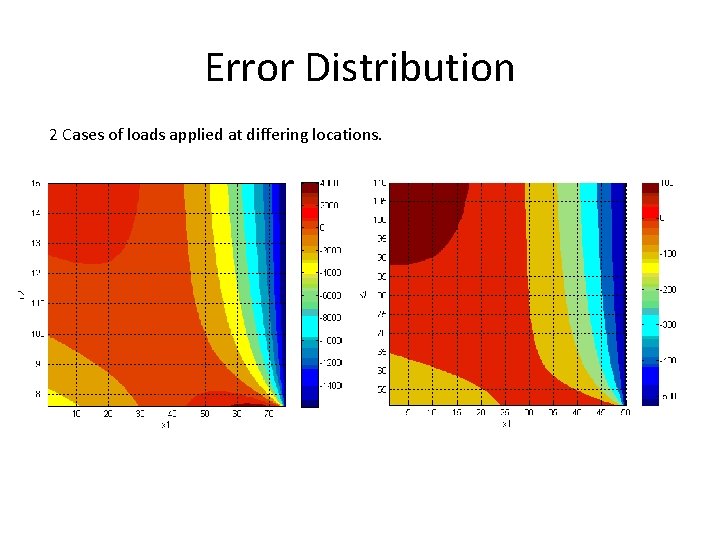
Error Distribution 2 Cases of loads applied at differing locations.

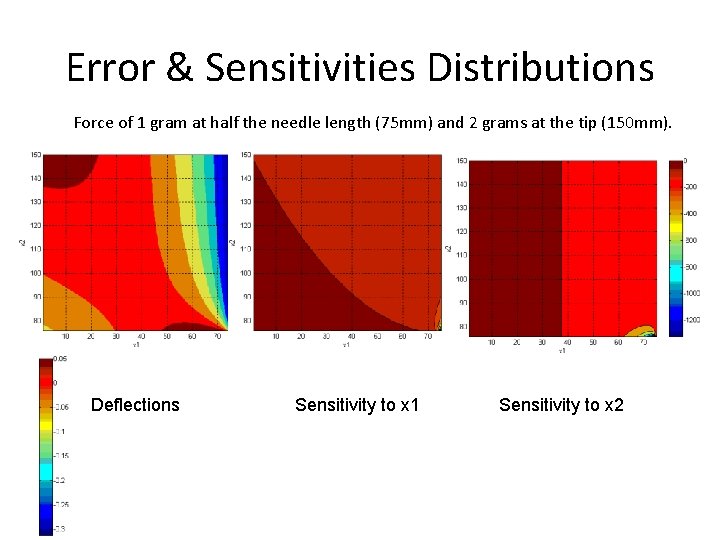
Error & Sensitivities Distributions Force of 1 gram at half the needle length (75 mm) and 2 grams at the tip (150 mm). Deflections Sensitivity to x 1 Sensitivity to x 2

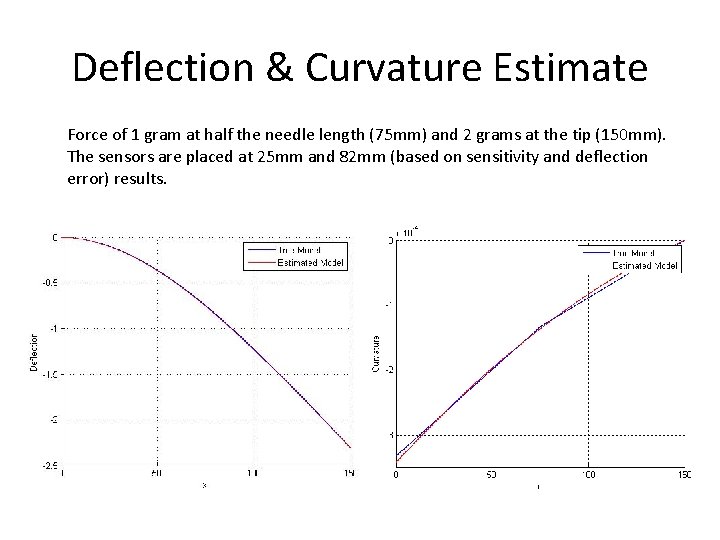
Deflection & Curvature Estimate Force of 1 gram at half the needle length (75 mm) and 2 grams at the tip (150 mm). The sensors are placed at 25 mm and 82 mm (based on sensitivity and deflection error) results.

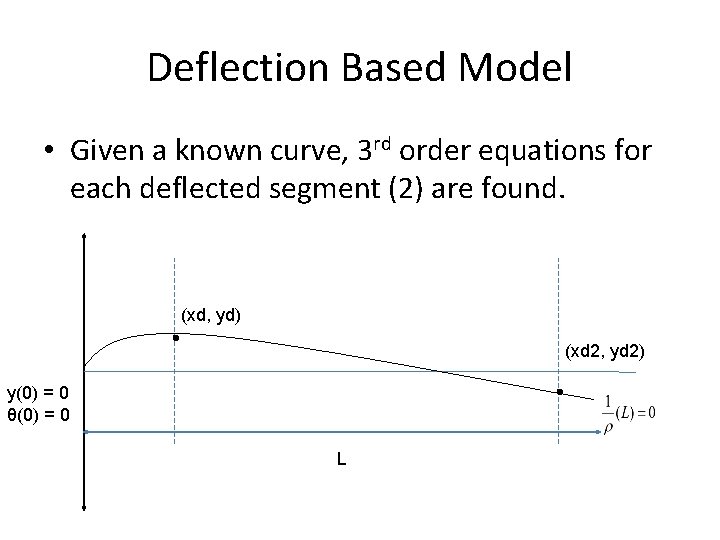
Deflection Based Model • Given a known curve, 3 rd order equations for each deflected segment (2) are found. (xd, yd) (xd 2, yd 2) y(0) = 0 θ(0) = 0 L

BC’s and System of Equations The system of equations to solve is: Because the deflection and slope at x = 0 is zero, the first equation has no first order or y-intercept terms. The continuity constraints are:

Finding Coefficients With at least the point of deflection and a point in the y 2 region, the system can be solved. A closer solution is found with more (x, y) points.

Deflection Based Method • Equations for Y 1 and Y 2 are found. • A true curvature model is found by taking the second derivative of the deflection. • An estimate curvature is calculated from the actual curvatures at two sensor positions. • Estimated deflection = ∫∫curvature.