Sensor Based Exploration Incremental Construction of the Hierarchical

Sensor Based Exploration: Incremental Construction of the Hierarchical Generalized Voronoi Graph

Why Sensor Based 1. Classical work is based on the assumption that a robot has a full knowledge of the world 2. The problem: realistic deployment of robots into unknown environments and into environments that are too difficult to model 3. Sensor based planning is important because: 1. the robot often has no priori knowledge of the world or may have only a coarse knowledge of the world 2. the world model is bound to contain inaccuracies or unexpected changes

This Algorithm 1. One of the first motion planning techniques that 1. relies only on line-of-sight sensor information. 2. functions in higher dimensions 3. offers completeness guarantees 2. A numerically well posed and complete algorithm for sensor based robot mapping of unknown environments. 3. The robot generates a small portion of the a roadmap edge and then follow this portion to generate the next segment. 4. The robot traces an edge until it reaches a node, at which it branches to explorer all edges emanating from that node. 1. When all nodes have no explored directions, the algorithm finishes.

Generalized Voronoi Graphs

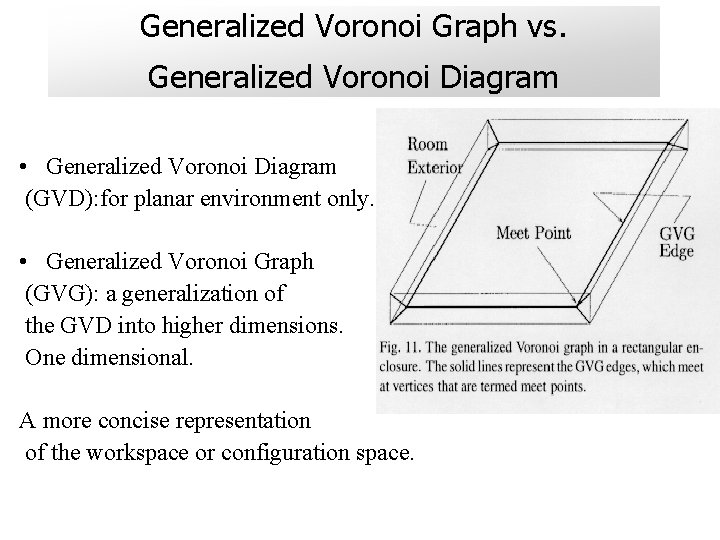
Generalized Voronoi Graph vs. Generalized Voronoi Diagram • Generalized Voronoi Diagram (GVD): for planar environment only. • Generalized Voronoi Graph (GVG): a generalization of the GVD into higher dimensions. One dimensional. A more concise representation of the workspace or configuration space.

Distance Function • Distance function: the distance between a point x and a convex set • Multi-object distance function: • All the above distance related function can be computed from sensor data directly.

Equidistant Face • The building block of the GVG is two-equidistant face:

Equidistant Face • Three-equidistant face: • By continuing intersection of the two-equidistant faces, a mequidistant face is formed, which is a one dimensional set of points. • A m+1 -equidistant face can be formed also, which is a meet point. • The GVG is the collection of m-equidistant faces(edges) and m+1 -equidistant faces(meet point).

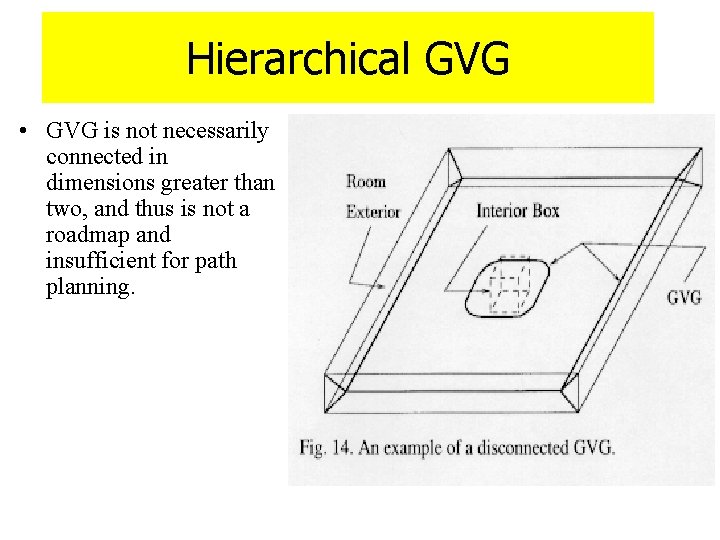
Hierarchical GVG • GVG is not necessarily connected in dimensions greater than two, and thus is not a roadmap and insufficient for path planning.

Hierarchical GVG • Higher order GVG is defined to connect the GVG: recursively defined on lower dimensional equidistant faces. • HGVG: the collection of all GVG and all higher order GVG. We will focus on R 3 only in the rest of this paper.

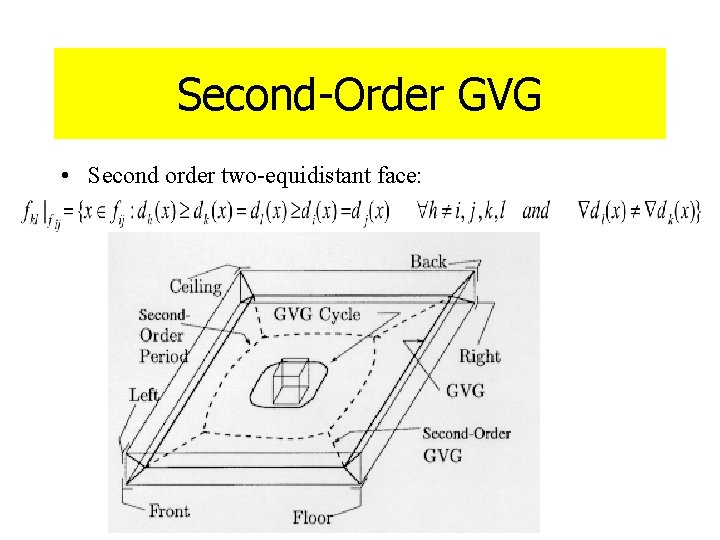
Second-Order GVG • Second order two-equidistant face:

Second-Order GVG • The cycle of the second order GVG implies the existence of GVG inside of it. • Linking from outer second order GVG to GVG is achieved via gradient descent of the distance to the second closest obstacle.

GVG Tracing Function • Edge tracing: trace the roots of the expression as is varied. x: point on the GVG. z 1: in the tangent direction of x. At x, let the hyperplane spanned by local coordinates z 2 -zm be termed the normal plane. The tracing function This function assumes a zero value only on the GVG.

GVG Edge Construction • edge construction: • predictor step: moves the robot for a small distance along the tangent direction of the GVG • corrector step: find the intersection of the GVG and the correcting plane. This is achieved through the Newton method: It can be proved that the Jacobian matrix is always nonsingular.

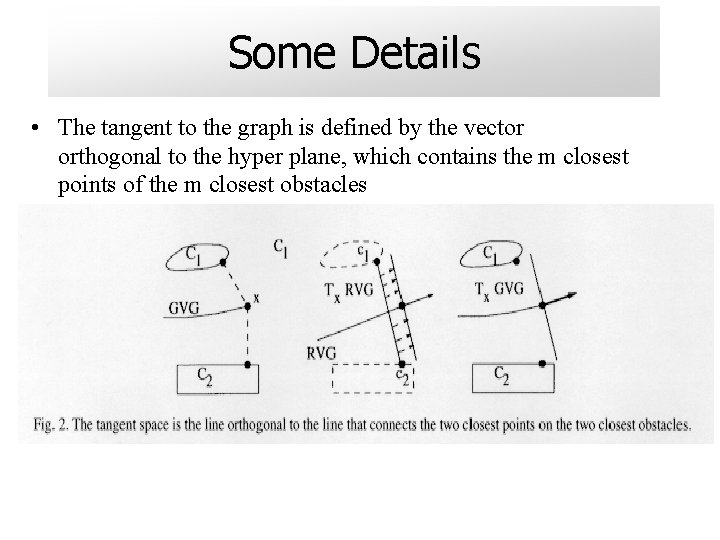
Some Details • The tangent to the graph is defined by the vector orthogonal to the hyper plane, which contains the m closest points of the m closest obstacles

Some Details • Meet point detection: by watching for an abrupt change in the direction of the gradients to the m closest obstacles. Accessibility: using gradient ascent on the multi-object distance function, moving in a direction to which the sensor with the smallest value is facing.

Construction of the Second. Order GVG • This section applies the same tracing method for GVG to trace the edges of second-order GVG. • The tracing function is: • Tangent direction: is the null space of the Jacobian of G 2:

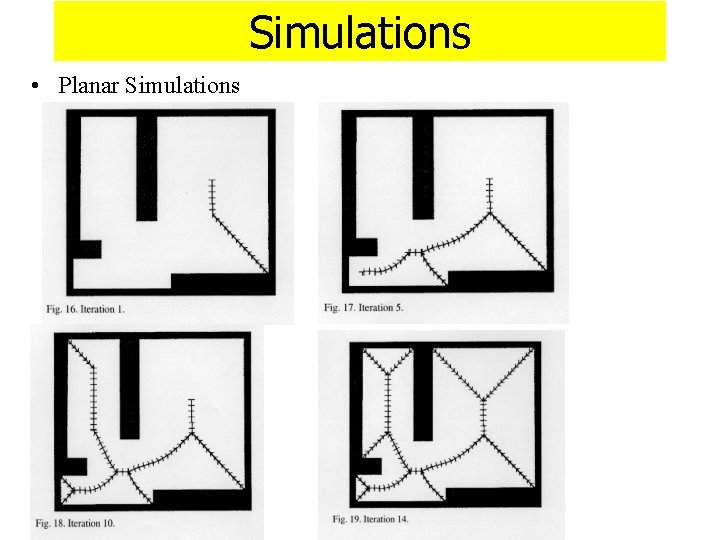
Simulations • Planar Simulations

19

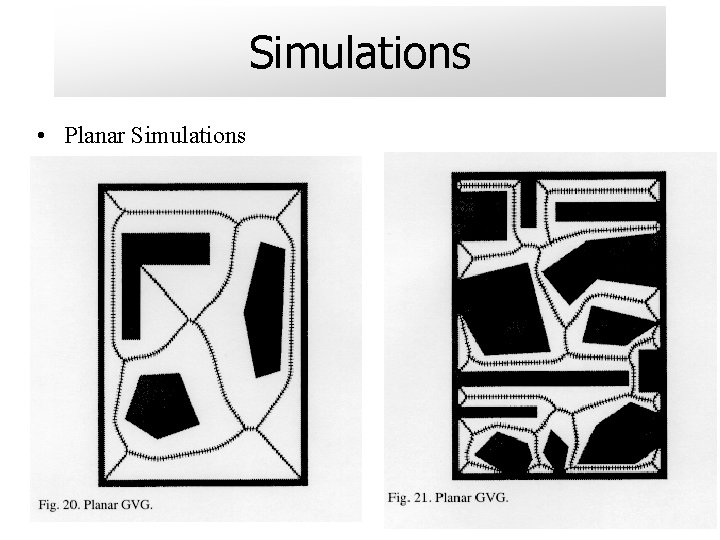
Simulations • Planar Simulations

Simulations • Three-Dimensional: GVG only, not connected; HGVG, GVG+GVG 2, connected

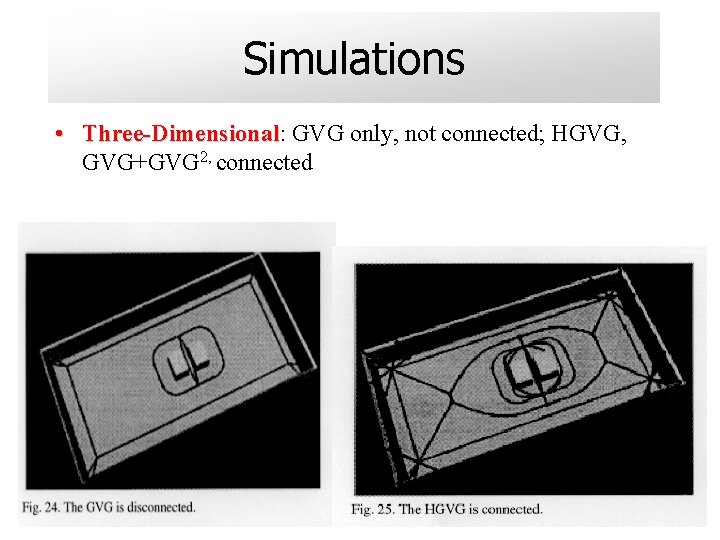
Simulations • Three-Dimensional: Three-Dimensional GVG only, not connected; HGVG, GVG+GVG 2, connected

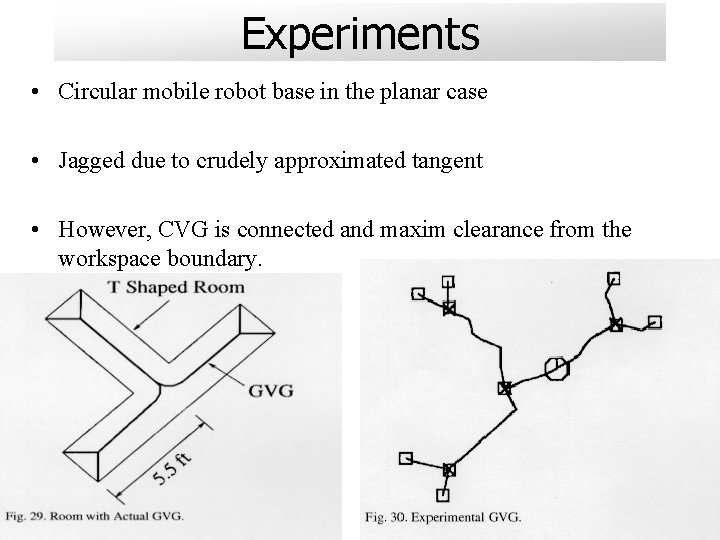
Experiments • Circular mobile robot base in the planar case • Jagged due to crudely approximated tangent • However, CVG is connected and maxim clearance from the workspace boundary.

Conclusions on GVG • An incremental procedure to construct the GVG and the HGVG is introduced • Requires only local sensor distance data • Future work: exploit geometries of the HGVG to locate itself on the partially explored map or conclude the robot has entered new territory.

The Basic Motion Problem

Let’s Assume… • We have an a priori map of the environment OR • We have sufficient sensor information to reconstruct the environment 26

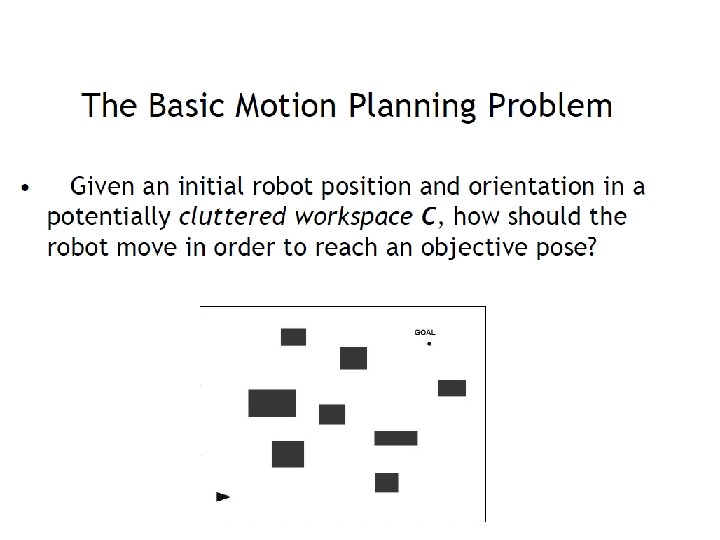
27

Supporting References • “Motion Planning Using Potential Fields, ” R. Beard & T. Mc. Clain, BYU, 2003 • You should download this from the course page and read it 28

Lecture Objectives • Examine alternate approaches to motion planning Roadmap Approach: – Visibility Graph Methods Cell Decomposition: – Exact Decomposition – Approximate: Uniform discretization & quadtree approaches Potential Fields

1. 2. 3. 4. 5. 6. 7. Sensor Based Algorithm Voronoi Diagrams Hierarchical Voronoi Diagrams Second Order Voronoi Diagrams Simulations The Basic Motion Problem 30

Sensor Based Exploration: Incremental Construction of the Hierarchical Generalized Voronoi Graph Howie Choset, Sean Walker, Kunnayut Eiamsa-Ard, Joel Burdick February 2000

32