Sensitive gas absorption coefficient measurements based on Q

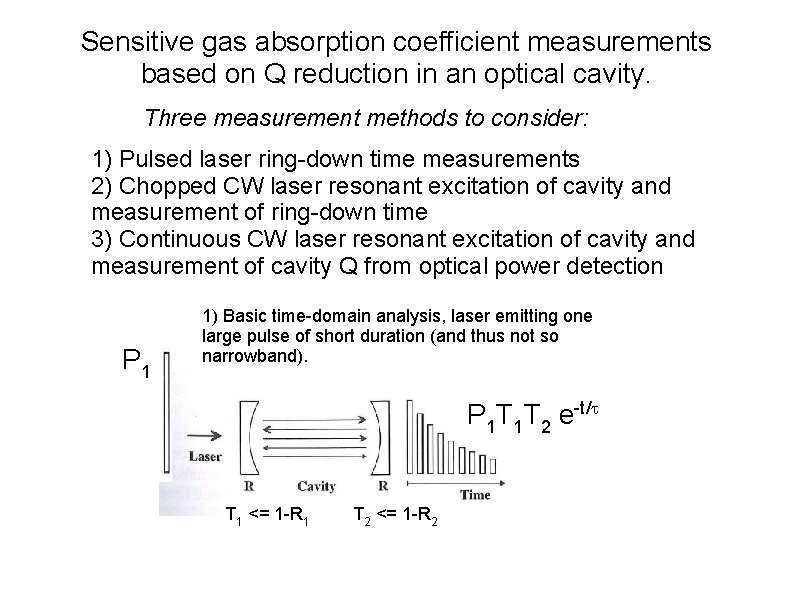
Sensitive gas absorption coefficient measurements based on Q reduction in an optical cavity. Three measurement methods to consider: 1) Pulsed laser ring-down time measurements 2) Chopped CW laser resonant excitation of cavity and measurement of ring-down time 3) Continuous CW laser resonant excitation of cavity and measurement of cavity Q from optical power detection P 1 1) Basic time-domain analysis, laser emitting one large pulse of short duration (and thus not so narrowband). P 1 T 1 T 2 e-t/ T 1 <= 1 -R 1 T 2 <= 1 -R 2

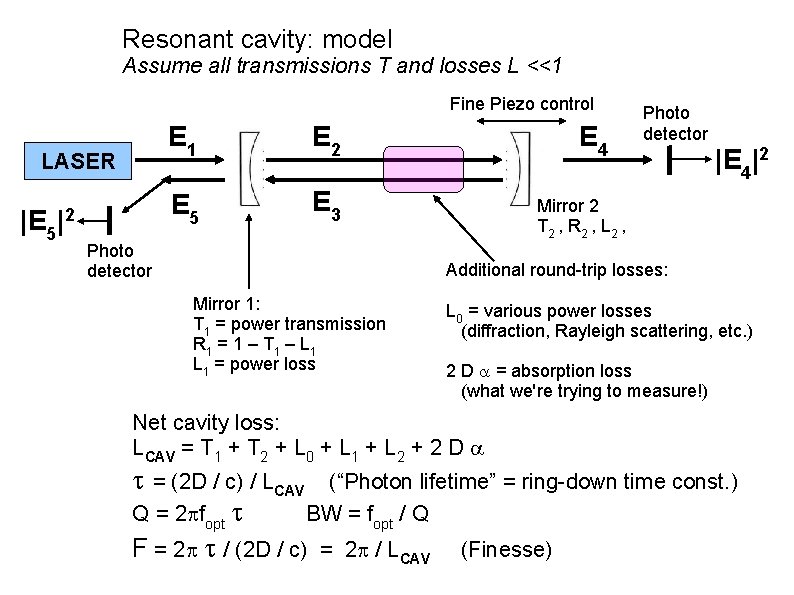
Resonant cavity: model Assume all transmissions T and losses L <<1 Fine Piezo control LASER |E 5 |2 E 1 E 2 E 5 E 3 Photo detector E 4 Photo detector |E 4|2 Mirror 2 T 2 , R 2 , L 2 , Additional round-trip losses: Mirror 1: T 1 = power transmission R 1 = 1 – T 1 – L 1 = power loss L 0 = various power losses (diffraction, Rayleigh scattering, etc. ) 2 D = absorption loss (what we're trying to measure!) Net cavity loss: LCAV = T 1 + T 2 + L 0 + L 1 + L 2 + 2 D = (2 D / c) / LCAV (“Photon lifetime” = ring-down time const. ) Q = 2 fopt BW = fopt / Q F = 2 / (2 D / c) = 2 / LCAV (Finesse)

D E 1 E 2 E 5 E 3 E 4 Intra-cavity waves E 2 and E 3 (at position of mirror 1 surface): E 3 * R 11/2 = (1 – LCAV / 2) ej 2 k. D E 2 = (1 – LCAV / 2) ej E 2 Resonance when = 0 (that is, 2 D = N ) Find that amplitude increased inside cavity at resonance: E 2 / E 1 = T 11/2 * 2 / LCAV On general principles: Since detection of sample absorption depends on loss of energy (photons) passing through sample, increasing the intracavity power |E 2|2 increases the potential detectivity.

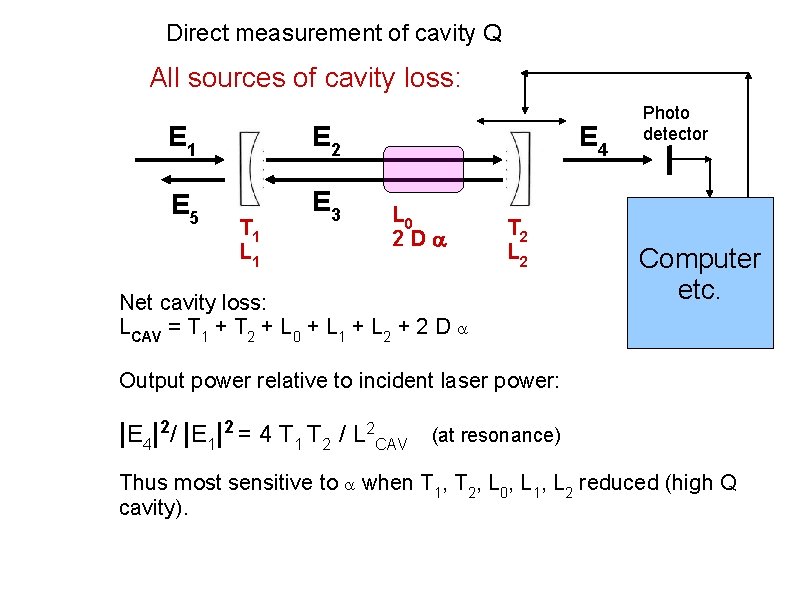
Direct measurement of cavity Q All sources of cavity loss: E 1 E 2 E 5 E 3 T 1 L 1 E 4 L 0 2 D T 2 L 2 Net cavity loss: LCAV = T 1 + T 2 + L 0 + L 1 + L 2 + 2 D Photo detector Computer etc. Output power relative to incident laser power: |E 4|2/ |E 1|2 = 4 T 1 T 2 / L 2 CAV (at resonance) Thus most sensitive to when T 1, T 2, L 0, L 1, L 2 reduced (high Q cavity).

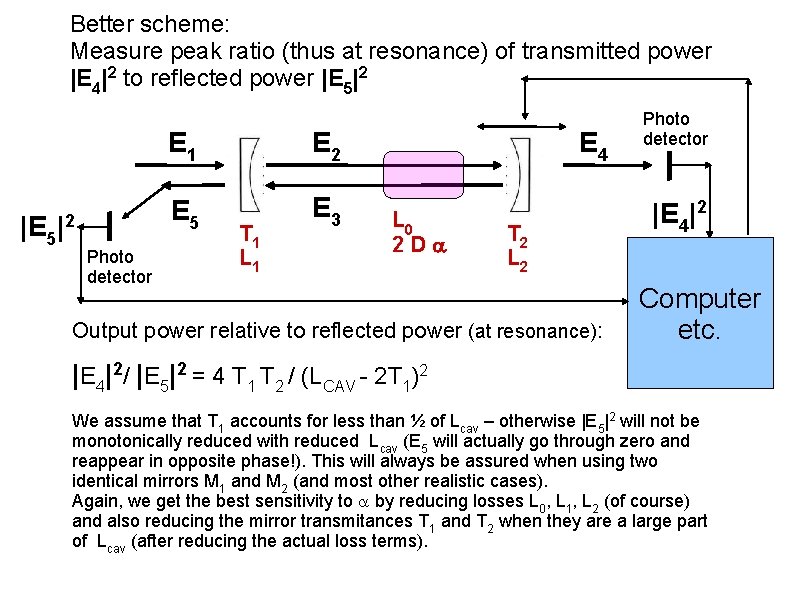
Better scheme: Measure peak ratio (thus at resonance) of transmitted power |E 4|2 to reflected power |E 5|2 |E 5 |2 Photo detector E 1 E 2 E 5 E 3 T 1 L 1 E 4 L 0 2 D T 2 L 2 Output power relative to reflected power (at resonance): Photo detector |E 4|2 Computer etc. |E 4|2/ |E 5|2 = 4 T 1 T 2 / (LCAV - 2 T 1)2 We assume that T 1 accounts for less than ½ of Lcav – otherwise |E 5|2 will not be monotonically reduced with reduced Lcav (E 5 will actually go through zero and reappear in opposite phase!). This will always be assured when using two identical mirrors M 1 and M 2 (and most other realistic cases). Again, we get the best sensitivity to by reducing losses L 0, L 1, L 2 (of course) and also reducing the mirror transmitances T 1 and T 2 when they are a large part of Lcav (after reducing the actual loss terms).

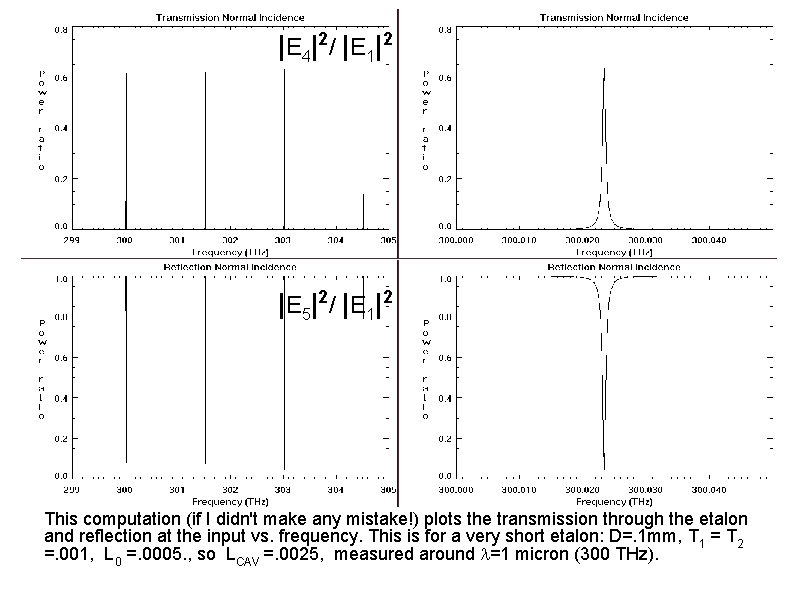
| E 4| 2/ | E 1| 2 | E 5| 2/ | E 1| 2 This computation (if I didn't make any mistake!) plots the transmission through the etalon and reflection at the input vs. frequency. This is for a very short etalon: D=. 1 mm, T 1 = T 2 =. 001, L 0 =. 0005. , so LCAV =. 0025, measured around =1 micron (300 THz).

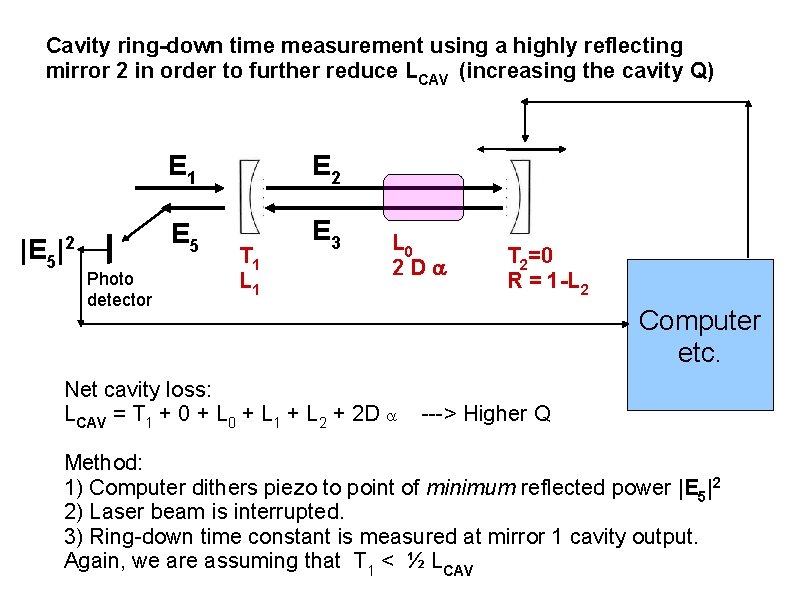
Cavity ring-down time measurement using a highly reflecting mirror 2 in order to further reduce LCAV (increasing the cavity Q) |E 5 |2 Photo detector E 1 E 2 E 5 E 3 T 1 L 0 2 D Net cavity loss: LCAV = T 1 + 0 + L 1 + L 2 + 2 D T 2=0 R = 1 -L 2 Computer etc. ---> Higher Q Method: 1) Computer dithers piezo to point of minimum reflected power |E 5|2 2) Laser beam is interrupted. 3) Ring-down time constant is measured at mirror 1 cavity output. Again, we are assuming that T 1 < ½ LCAV

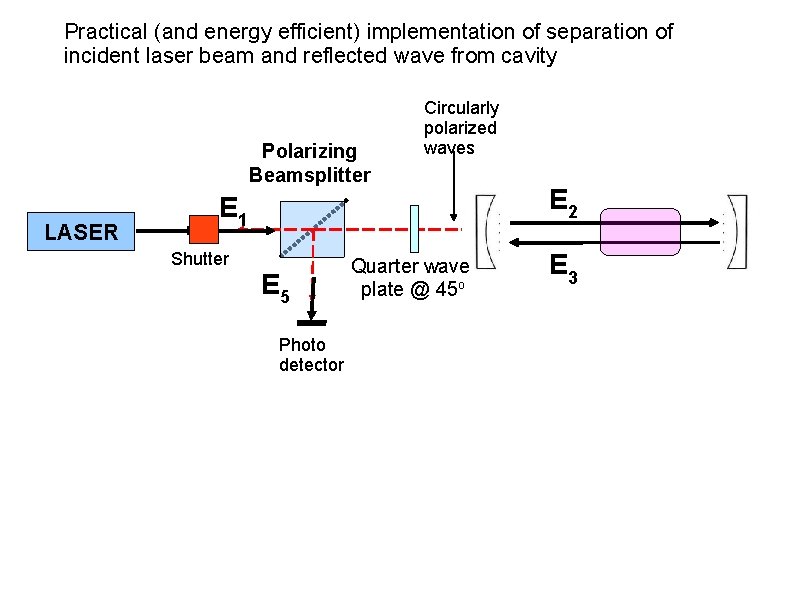
Practical (and energy efficient) implementation of separation of incident laser beam and reflected wave from cavity Polarizing Beamsplitter LASER Circularly polarized waves E 1 Shutter E 5 Photo detector Quarter wave plate @ 45 o E 2 E 3