Seminar on Geometric Approximation Algorithms Speaker Alon Horowitz

Seminar on Geometric Approximation Algorithms Speaker: Alon Horowitz

Outline of this lecture • What is WSPD • How to construct and represent WSPD efficiently • Applications of WSPD

What is WSPD • Let P be a set of n points in Rd, and ¼ > ɛ > 0 a parameter. • Say we want to represent all distances between points of P. Return all pairwise distances Return all n points in P (of size dn)

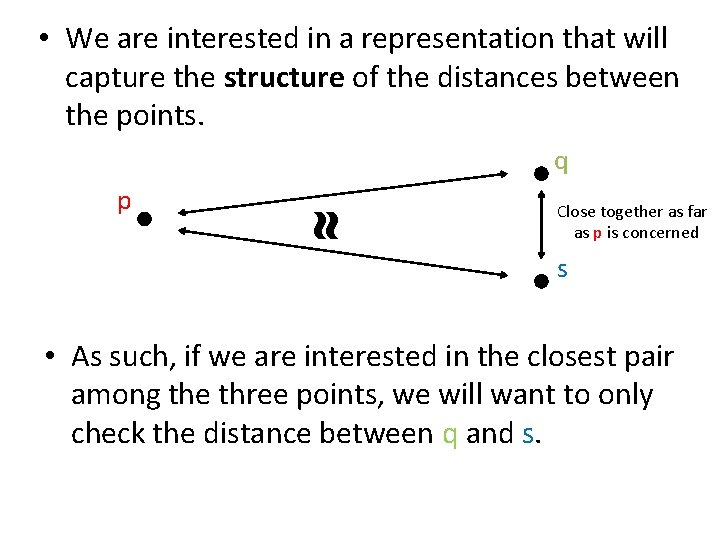
• We are interested in a representation that will capture the structure of the distances between the points. q ≈ p Close together as far as p is concerned s • As such, if we are interested in the closest pair among the three points, we will want to only check the distance between q and s.

Definitions • Denote by the set of all the (unordered) pairs of points formed by the sets A and B. • We will be informal and refer to as a pair of sets A and B. • Example: {1, 2, 3} = {{1, 2}, {1, 3}, {2, 3}}

Definitions • For a point set P, a pair decomposition of P is a set of pairs such that: 1. Ai , Bi P for every i 2. Ai ∩ Bi = ɸ for every i 3. • Translation: For any pair of distinct points p, q ϵ P, there is at least one pair {Ai , Bi} ϵ such that p ϵ Ai and q ϵ Bi

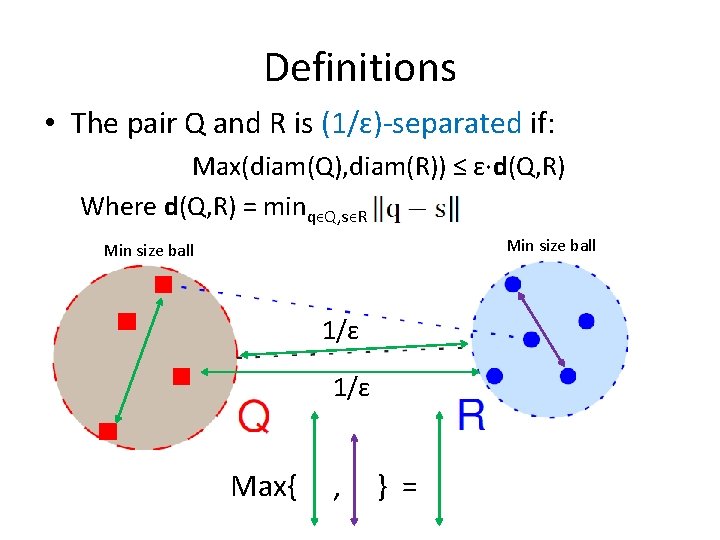
Definitions • The pair Q and R is (1/ɛ)-separated if: Max(diam(Q), diam(R)) ≤ ɛ∙d(Q, R) Where d(Q, R) = minqϵQ, sϵR Min size ball 1/ɛ Max{ , } =

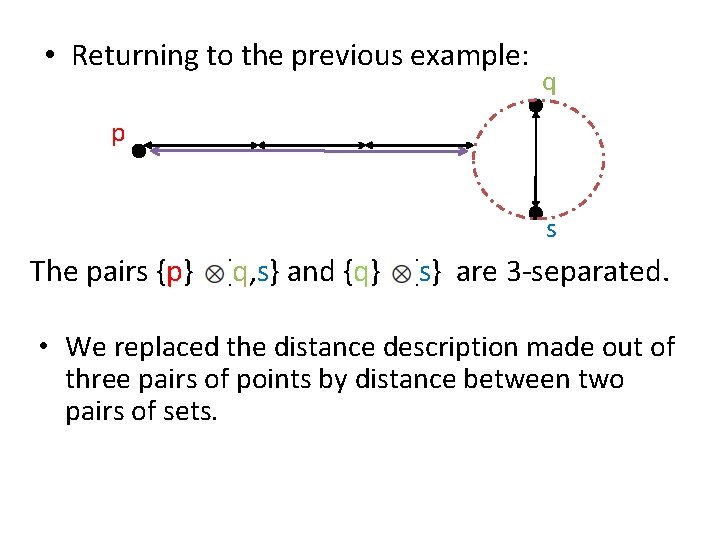
• Returning to the previous example: q p s The pairs {p} {q, s} and {q} {s} are 3 -separated. • We replaced the distance description made out of three pairs of points by distance between two pairs of sets.

Definitions • For a point set P, a well-separated pair decomposition (WSPD) of P with parameter 1/ɛ is a pair decomposition of P with a set of pairs: such that, for any i, the sets Ai and Bi are -separated. • In the last example we got: = { {{p}, {q, s}} , {{q}, {s}} } 1/ɛ

How to construct and represent WSPD efficiently • Representation • Construction algorithm • Analysis

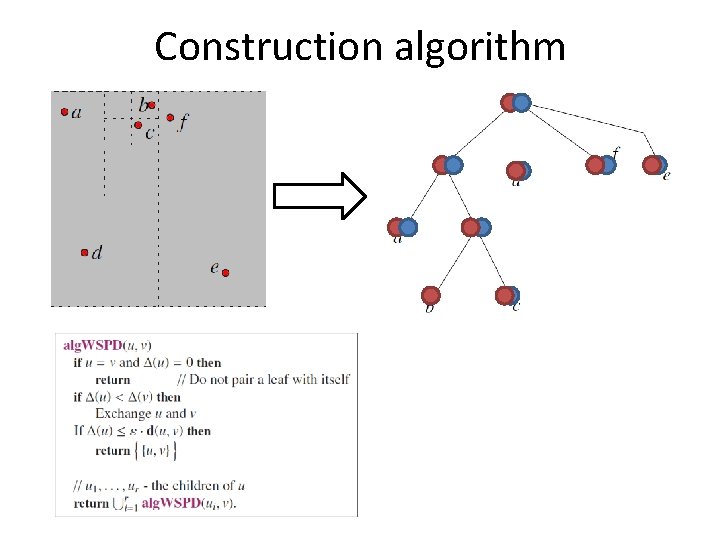
Representation • Instead of maintaining such decomposition explicitly, it is convenient to construct a tree T having the points of P as leaves. u V P = {a, b, c, d, e, f} (Ai , Bi) = (Pv , Pu) = ({b, c} , {e}) • Now every pair (Ai , Bi) is just a pair of nodes (v , u) of T, such that Ai = Pv and Bi = Pu , where Pv denotes the points of P stored in the subtree of v.

Representation • In our case, the tree we would use is a compressed quadtree of P. The diameter of a point set stored in a node drops quickly • There are many possible WSPDs that can be represented using the tree. • We will try to find a WSPD that is “minimal”.

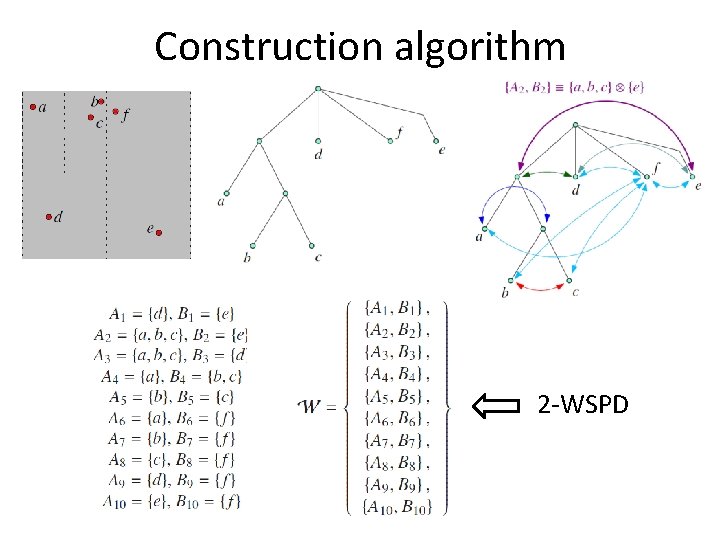
Construction algorithm Given a point set P in Rd: • Compute the compressed quadtree T of P. • Greedy – tries to put into the WSPD pairs of nodes in the tree that are as high as possible: – Start from root (The pair {root, root}). – Check if current pair is well separated. – If not, replace the bigger node (diameter wise) with his children.

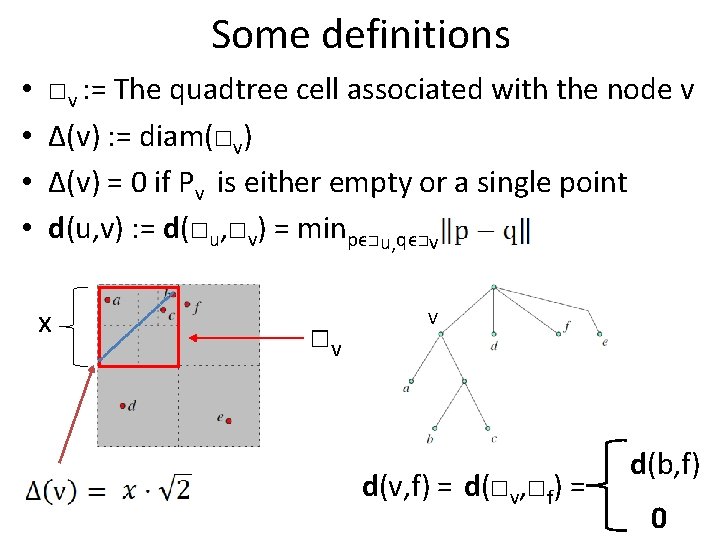
Some definitions • • □v : = The quadtree cell associated with the node v Δ(v) : = diam(□v) Δ(v) = 0 if Pv is either empty or a single point d(u, v) : = d(□u, □v) = minpϵ□u, qϵ□v x □v V d(v, f) = d(□v, □f) = d(b, f) 0

Construction algorithm

Construction algorithm

Construction algorithm 2 -WSPD

Analysis • • • alg. WSPD terminates alg. WSPD Computes a valid pair-decomposition The computed pairs are (1/ɛ)-separated The number of computed pairs is O(n/ɛd) (1/ɛ)-WSPD construction time is O(nlogn + n/ɛd)

alg. WSPD terminates • • If u, v are leaves then Δ(u) = 0 and Δ(v) = 0 Δ(u) ≤ ɛ∙d(u, v) True Always stops if both u and v are leafs Always terminates

alg. WSPD Computes a valid pair-decomposition • Reminder: For a point set P, a pair decomposition of P is a set of pairs such that: 1. Ai , Bi P for every i 2. Ai ∩ Bi = ɸ for every i 3. • 1. For every i, Ai , Bi corresponds to some Pu , Pv and by definition Pu , Pv P. • 3. Every pair of points of P is covered by a pair of subsets {Pu , Pv} output by the alg. WSPD algorithm By induction…

alg. WSPD Computes a valid pair-decomposition • 2. Let {u, v} be an output pair • If Pu and Pv are single point, then Pu ϶ x ≠ y ϵ Pv because of the first line in alg. WSPD Pu∩Pv =ɸ • If Pu or Pv are not single point, then: a: = max(diam(Pu), diam(Pv)) > 0 This implies that: d(Pu, Pv) ≥ d(□u, □v) = d(u, v) ≥ Δ(u)/ɛ ≥ a/ɛ > 0 Pu∩Pv =ɸ

The computed pairs are (1/ɛ)-separated • Reminder: The pair Q and R is (1/ɛ)-separated if: Max(diam(Q), diam(R)) ≤ ɛ∙d(Q, R) Where d(Q, R) = minqϵQ, sϵR • Proof: for every output pair {u, v}, we have by the design of the algorithm that: Max(diam(Pu), diam(Pv)) ≤ max{Δ(u), Δ(v)} ≤ ɛ∙d(u, v) Also, for any qϵPu and sϵPv we have: d(u, v) = d(□u, □v) ≤ d(Pu, Pv) ≤ d(q, s) since Pu □u and Pv □v

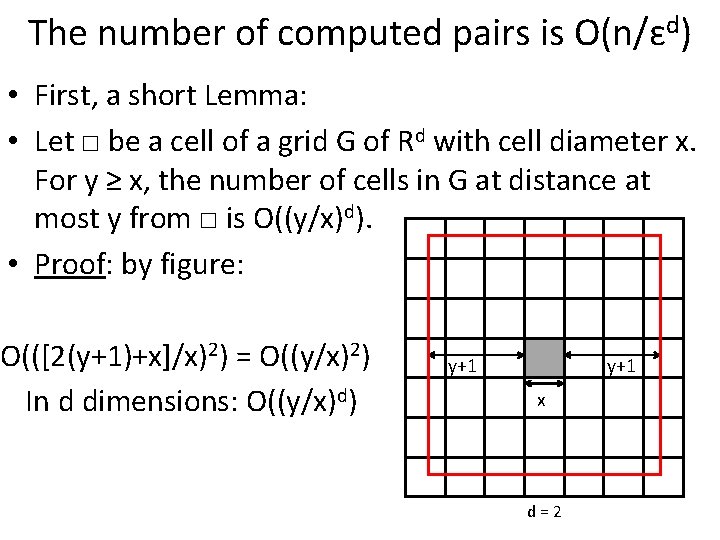
The number of computed pairs is O(n/ɛd) • First, a short Lemma: • Let □ be a cell of a grid G of Rd with cell diameter x. For y ≥ x, the number of cells in G at distance at most y from □ is O((y/x)d). • Proof: by figure: O(([2(y+1)+x]/x)2) = O((y/x)2) In d dimensions: O((y/x)d) y+1 x d=2

The number of computed pairs is O(n/ɛd) • Proof: Let {u, v} be a pair appearing in the output • Let's consider the sequence of recursive calls that led to this output. In particular, Let's assume that the last recursive call to alg. WSPD(u, v) was issued by alg. WSPD(u, v’), where v’ = p(v) (the parent of v in T) • This implies that Δ(u) ≤ Δ(v’) • Furthermore, the fact that alg. WSPD(u, v’) was invoked implies that alg. WSPD(p(u), a(v’)) has been considered and then p(u) was split. • This implies that Δ(a(v’)) ≤ Δ(p(u)) • To summarize: Δ(u) ≤ Δ(v’) ≤ Δ(a(v’)) ≤ Δ(p(u))

The number of computed pairs is O(n/ɛd) • Let us prove that each node v’ is charged at most O(1/ɛd) times • Since the pair {u, v’} was not output by alg. WSPD (despite being considered), we conclude: Δ(v’) > ɛ∙d(u, v) < Δ(v’)/ɛ : = r • Because we proved: Δ(u) ≤ Δ(v’) ≤ Δ(p(u)) then there are 3 possibilities: – Δ(u) = Δ(v’) – Δ(v’) = Δ(p(u)) – Δ(u) < Δ(v’) < Δ(p(u)) Possible?

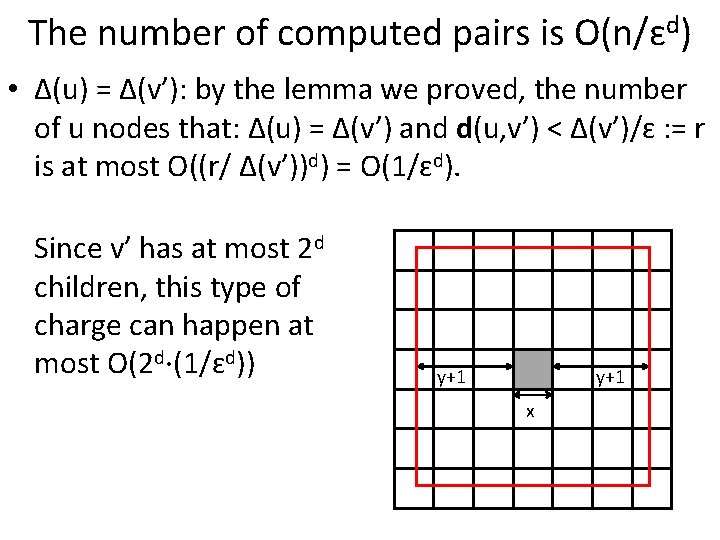
The number of computed pairs is O(n/ɛd) • Δ(u) = Δ(v’): by the lemma we proved, the number of u nodes that: Δ(u) = Δ(v’) and d(u, v’) < Δ(v’)/ɛ : = r is at most O((r/ Δ(v’))d) = O(1/ɛd). Since v’ has at most 2 d children, this type of charge can happen at most O(2 d∙(1/ɛd)) y+1 x

The number of computed pairs is O(n/ɛd) • Δ(v’) = Δ(p(u)): by the same argument, the number of p(u) nodes that: d(p(u), v’) ≤ d(u, v’) < r is at most O(1/ɛd). Since also p(u) has at most 2 d children at most O(2 d∙ 2 d∙(1/ɛd)) • Δ(u) < Δ(v’) < Δ(p(u)): Let □’ be the cell in G containing □u. Observe that □u □’ □p(u). In addition: d(□’, □v’) ≤ d(□u, □v’) = d(u, v’) < r. As before, it follows that there at most O(1/ɛd) cells like □’, and as before, total number of charges is at most O(2 d∙(1/ɛd)). □’ □p(u) □u □v’

The number of computed pairs is O(n/ɛd) • In conclusion, v’ can be charged at most O(2 d∙ 2 d∙(1/ɛd)) = O(1/ɛd) times. • Since there are O(n) nodes in T, the total number of pairs generated by alg. WSPD is O(n/ɛd). • Every point of P is present in O(1/ɛd) pairs. • Since running time of alg. WSPD is linear in the output size, and quadtree construction time is O(nlogn) we conclude: (1/ɛ)-WSPD construction time is O(nlogn + n/ɛd)

Applications of WSPD • • Closest pair All nearest neighbors Spanners Approximating the Minimum Spanning Tree

Closest pair • Let P be a set of points in Rd, we would like to compute the closest pair. • Lemma: let W be a (1/ɛ)-WSPD of P, for ɛ ≤ ½. There exists a pair {u, v}ϵW, such that: – |Pu| = |Pv| = 1 – is the distance of the closest pair.

Closest pair • Proof: Let p, q be the closest pair and let {u, v}ϵW be the pair such that pϵPu and qϵPv • Let assume by contradiction that there is an additional point sϵ Pu Contradiction to p, q being the closest pair

Closest pair Algorithm: • Compute 2 -WSPD of P • Scan all pairs of W • Compute distance between pairs {u, v} which are singletons • Return the closest pair encountered

All nearest neighbors • Given a set P of points in Rd, we would like to compute for each point qϵP its nearest neighbor in P. • Is nearest neighbor a symmetrical relationship? q is the nearest neighbor to p, but s is the nearest neighbor to q

All nearest neighbors Algorithm: • Compute 4 -WSPD of P • Scan all pairs of W • Compute distance between pairs {u, v} such that Pu or Pv is a singleton • For each Pu = {p}, record for p the closest point to it in Pv • Return the recorded nearest point for every point p in P

All nearest neighbors • Lemma: Let p be a point in P and let q be the nearest neighbor to p in P{p}, then there exists a pair {u, v}ϵW such that Pu={p} and qϵPv • Proof: Consider {u, v}ϵW such that pϵPu and qϵPv Diam(Pu) ≤ ɛd(Pu, Pv) ≤ ɛ||p-q|| ≤ ||p-q||/4 • If Pu contained any other point except p then contradiction to q being the nearest neighbor to p

All nearest neighbors • Let P be a set of n points in the plane, then one can solve the all nearest neighbor problem, in O(n(logn + logɸ(P)) time, where ɸ is the spread of P • Difficulties: according to the algorithm: § Compute distance between pairs {u, v} such that Pu or Pv is a singleton § For each Pu = {p}, record for p the closest point to it in Pv • What if Pv is very big? ? ?

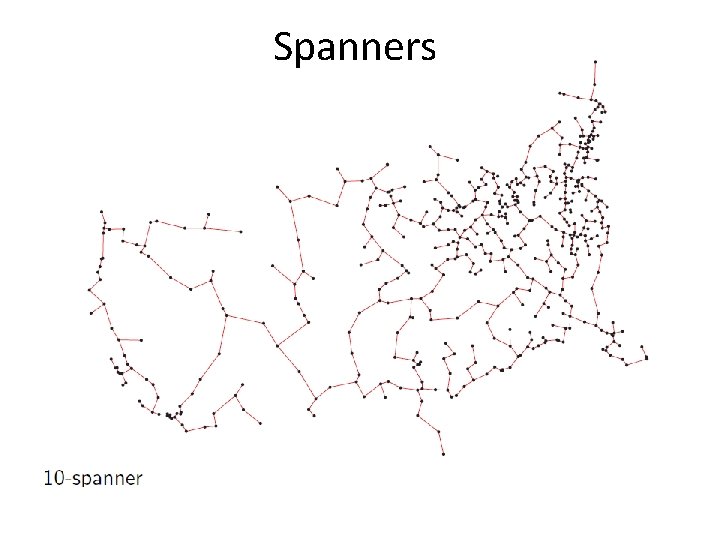
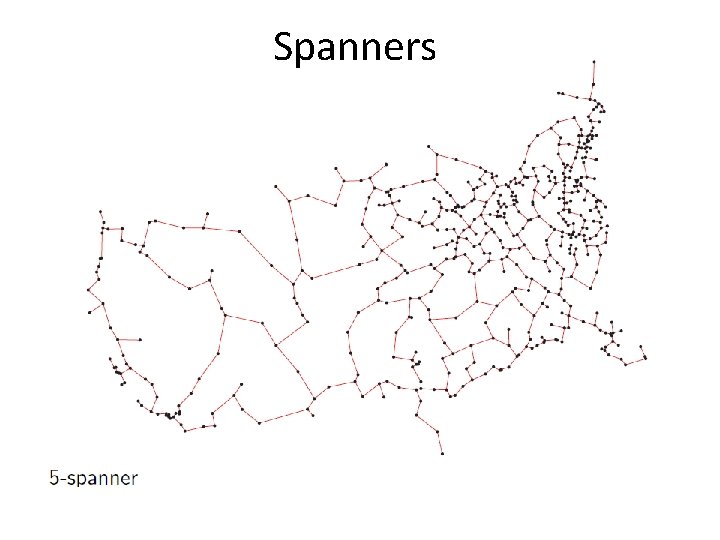
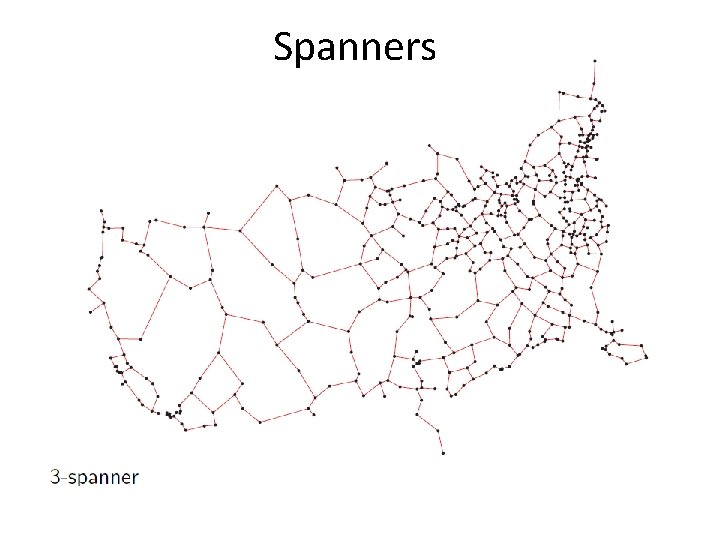
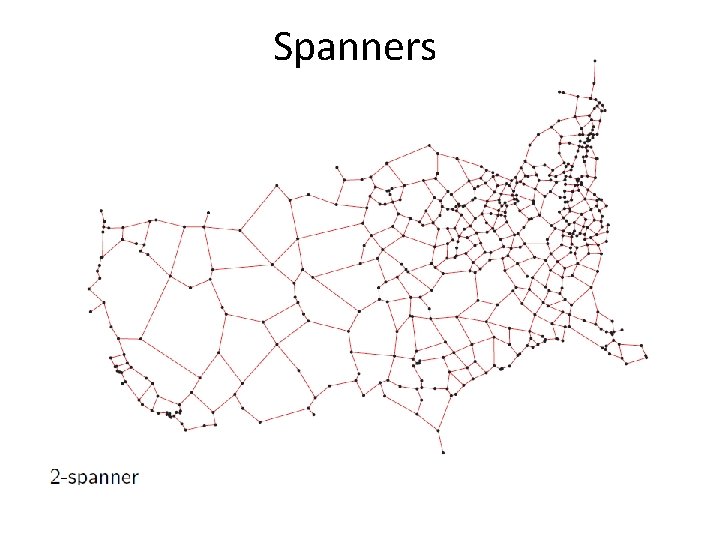
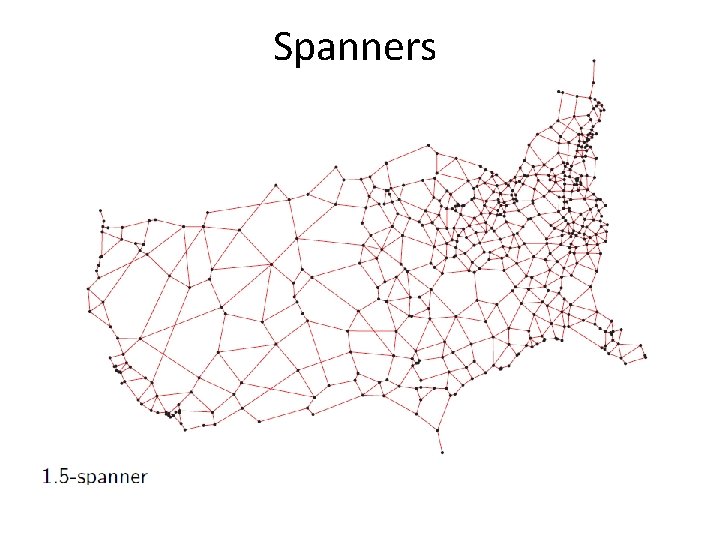
Spanners Definitions: • d. G(q, s) : = distance of the shortest path between vertices q, s in weighted graph G. • A t-spanner of a set of points P in Rd is a weighted graph G whose vertices are the points of P, and for any q, sϵP, we have: v d. G is a metric (complies with the triangle inequality)

Spanners • Let P be a set of n points in Rd and let 1 ≥ ɛ > 0 be a parameter • we would like to compute a (1+ɛ)-spanner of P with O(n/ɛd) edges in O(nlogn + n/ɛd) time • (1+ɛ)-spanners approximate the complete graph with a relative error ɛ

Spanners

Spanners

Spanners

Spanners

Spanners

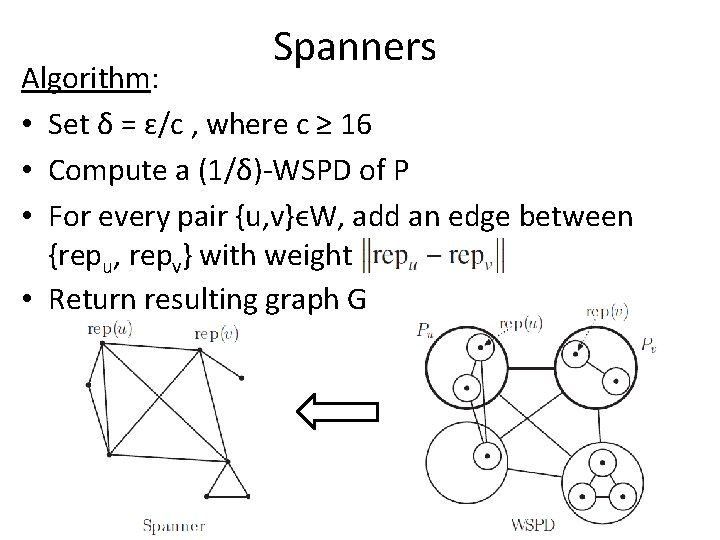
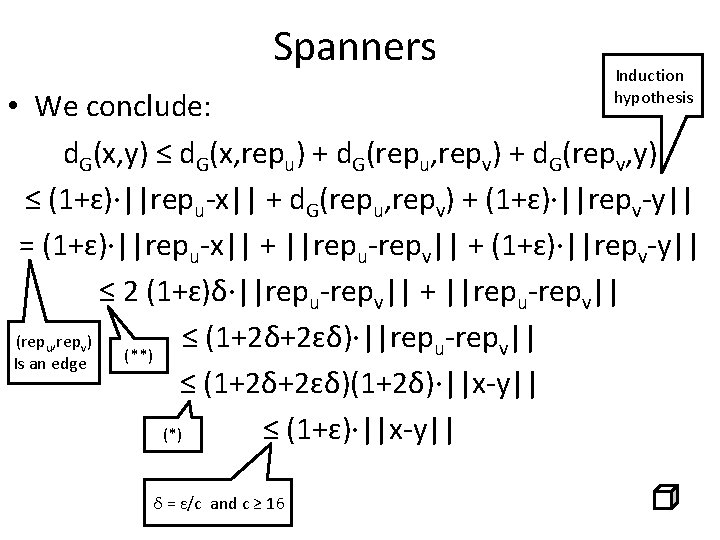
Spanners Algorithm: • Set δ = ɛ/c , where c ≥ 16 • Compute a (1/δ)-WSPD of P • For every pair {u, v}ϵW, add an edge between {repu, repv} with weight • Return resulting graph G

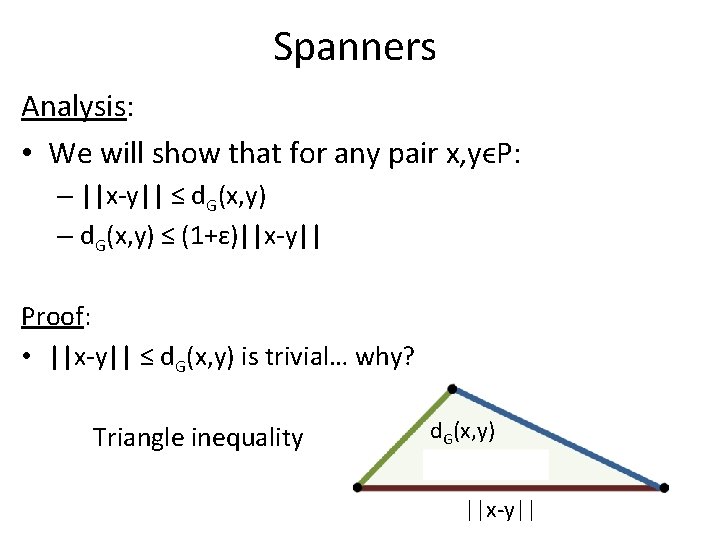
Spanners Analysis: • We will show that for any pair x, yϵP: – ||x-y|| ≤ d. G(x, y) – d. G(x, y) ≤ (1+ɛ)||x-y|| Proof: • ||x-y|| ≤ d. G(x, y) is trivial… why? Triangle inequality d. G(x, y) ||x-y||

Spanners • d. G(x, y) ≤ t||x-y|| by induction on the distance of the pairs: • Let's assume that for any pair z, wϵP: ||z-w||<||x-y|| d. G(z, w) ≤ (1+ɛ)||z-w|| • The pair x, y must appear in some pair {u, v}ϵW, where xϵPu and yϵPv , thus: (*) • Also: (**)

Spanners Induction hypothesis • We conclude: d. G(x, y) ≤ d. G(x, repu) + d. G(repu, repv) + d. G(repv, y) ≤ (1+ɛ)∙||repu-x|| + d. G(repu, repv) + (1+ɛ)∙||repv-y|| = (1+ɛ)∙||repu-x|| + ||repu-repv|| + (1+ɛ)∙||repv-y|| ≤ 2 (1+ɛ)δ∙||repu-repv|| + ||repu-repv|| ≤ (1+2δ+2ɛδ)∙||rep -rep || (rep , rep ) u v (**) Is an edge ≤ (1+2δ+2ɛδ)(1+2δ)∙||x-y|| ≤ (1+ɛ)∙||x-y|| (*) u v δ = ɛ/c and c ≥ 16

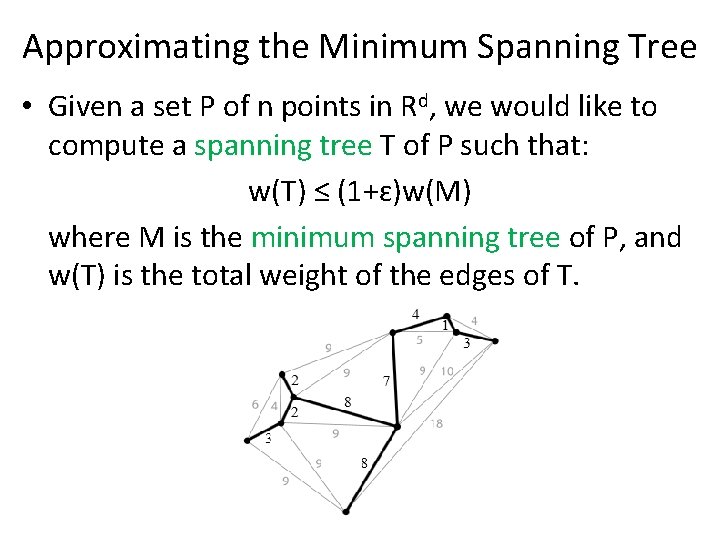
Approximating the Minimum Spanning Tree • Given a set P of n points in Rd, we would like to compute a spanning tree T of P such that: w(T) ≤ (1+ɛ)w(M) where M is the minimum spanning tree of P, and w(T) is the total weight of the edges of T.

Approximating the Minimum Spanning Tree Algorithm: • Compute a (1+ɛ)-spanner G of P • Compute the minimum spanning tree T of G • Return T as the approximate minimum spanning tree Running Time: • Computing a minimum spanning tree of a graph, with n vertices and m edges takes O(nlogn + m) time Computing T takes O(nlogn + n/ɛd) time

Approximating the Minimum Spanning Tree • We need to prove that T is the required approximation Proof: • π(q, s) : = shortest path between q and s in G • M: = the minimum spanning tree of P • Since G is a (1+ɛ)-spanner, for any q, sϵP: w(π(q, s)) ≤ (1+ɛ)||q-s|| • Let’s look at G’ = (P, E) which is a connected subgraph of G, where E =

Approximating the Minimum Spanning Tree • Since G is a (1+ɛ)-spanner: • Since G’ is a connected spanning subgraph of G: w(T) ≤ w(G’) ≤ (1+ɛ)w(M)

That’s All… 100 points On a Circle