Seminar 1 Efficient Algorithms for Molecular Dynamics Simulation

Seminar 1: Efficient Algorithms for Molecular Dynamics Simulation Andrew Noske

About the Project Part of TOMSK (Towards Molecular Structure Kinetics) Build an “engine layer” for particle simulations

About Molecular Simulations Real molecules obey quantum laws… but can approximate with classical laws. n e. g. : Newton’s law: force=mass*acceleration Molecular Dynamics (MD): integrates equations of motion of atoms each timestep. n Cannot predict precisely what will happen: generates statistical prediction.

Chosen Interaction Model Lennard Jones Potential Pair Equation: I will use this to simulate atoms in a stable liquid. NOTE: Will be easy to overwrite/change interaction model & add statistical analysis functions (e. g. : calc Temperature).

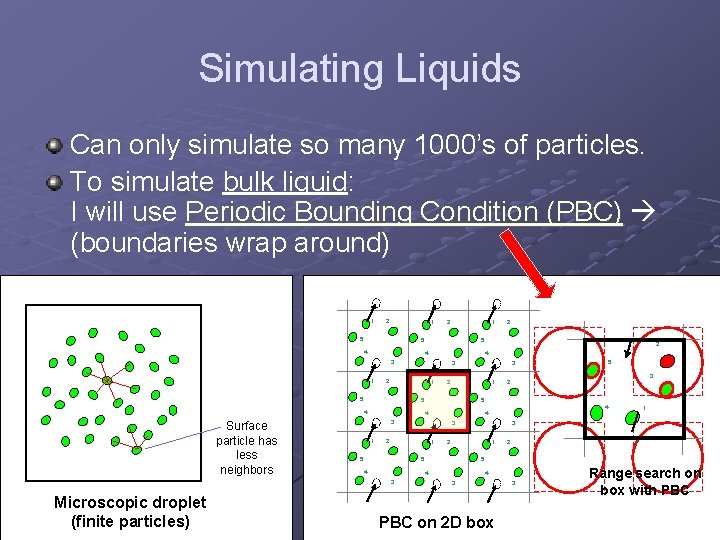
Simulating Liquids Can only simulate so many 1000’s of particles. To simulate bulk liquid: I will use Periodic Bounding Condition (PBC) (boundaries wrap around) 1 2 1 5 2 5 4 1 1 1 4 3 2 1 1 3 2 1 5 4 3 2 4 3 5 5 5 4 2 5 4 3 Microscopic droplet (finite particles) 3 2 5 4 1 2 4 3 2 5 4 3 Surface particle has less neighbors 1 4 3 PBC on 2 D box 3 Range search on box with PBC

N-body Problem N-body problem: all (N) particles in a system have pair-wise interaction. Consider ALL Solutions: n Brute force approach compare all pairs O(N 2) n Better approach: approximate distant forces Lead to many specific solutions. Approximate

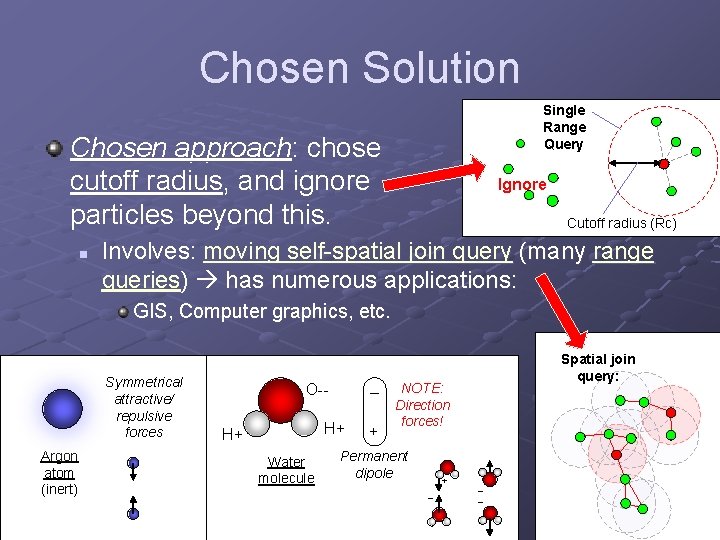
Chosen Solution Single Range Query Chosen approach: chose cutoff radius, and ignore particles beyond this. n Ignore Cutoff radius (Rc) Involves: moving self-spatial join query (many range queries) has numerous applications: GIS, Computer graphics, etc. Symmetrical attractive/ repulsive forces Argon atom (inert) O-- – H+ H+ Water molecule + Spatial join query: NOTE: Direction forces! Permanent dipole + – – –

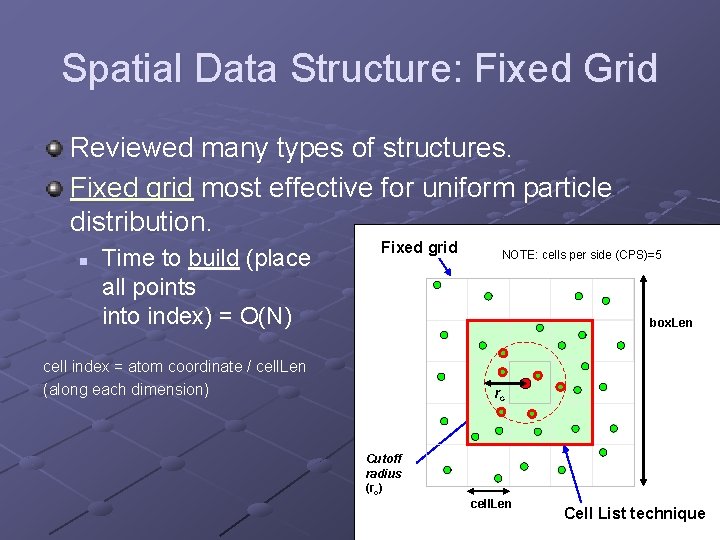
Spatial Data Structure: Fixed Grid Reviewed many types of structures. Fixed grid most effective for uniform particle distribution. n Time to build (place all points into index) = O(N) Fixed grid NOTE: cells per side (CPS)=5 box. Len cell index = atom coordinate / cell. Len (along each dimension) rc Cutoff radius (rc) cell. Len Cell List technique

Scientific Process Using Visual C++ console application. n n Am using OO principles. Have read “Effective C++” & now reading “More Effective C++”. Testing process: n n Run a series of simulations in batch… Output results to CSV… including: grid parameters, clock tics elapsed, primary focus distance calculates, & more n n Analyze/graph CSV using Excel. Can be time consuming!

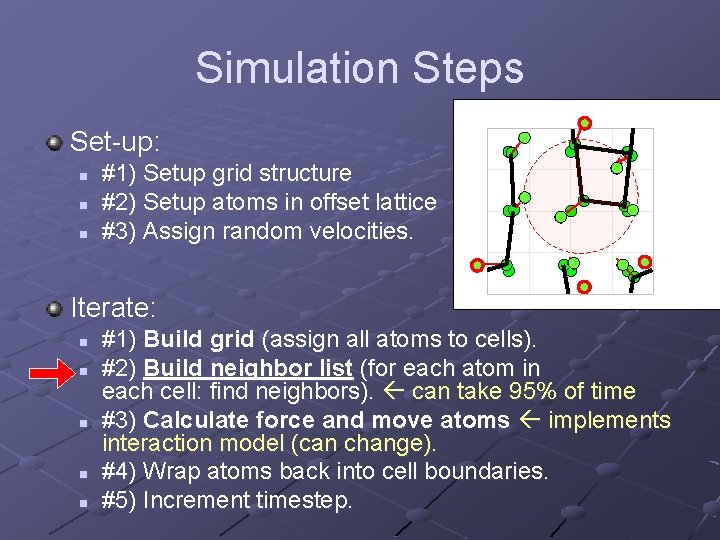
Simulation Steps Set-up: n n n #1) Setup grid structure #2) Setup atoms in offset lattice #3) Assign random velocities. Iterate: n n n #1) Build grid (assign all atoms to cells). #2) Build neighbor list (for each atom in each cell: find neighbors). can take 95% of time #3) Calculate force and move atoms implements interaction model (can change). #4) Wrap atoms back into cell boundaries. #5) Increment timestep.

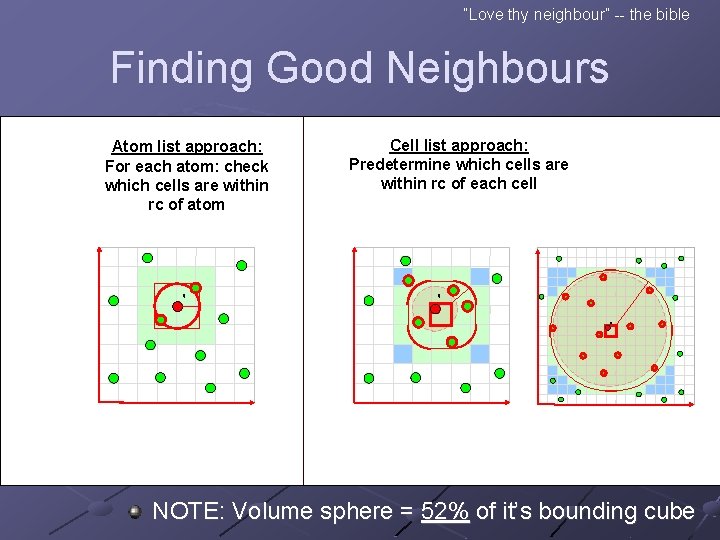
“Love thy neighbour” -- the bible Finding Good Neighbours Atom list approach: For each atom: check which cells are within rc of atom q Cell list approach: Predetermine which cells are within rc of each cell q q NOTE: Volume sphere = 52% of it’s bounding cube

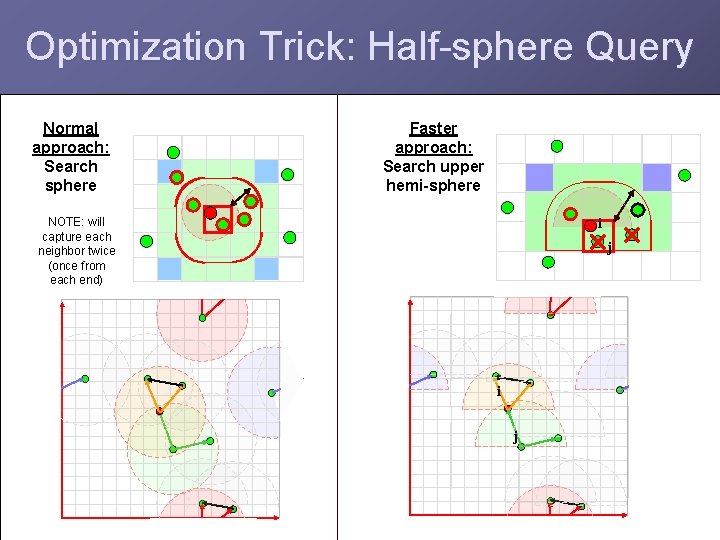
Optimization Trick: Half-sphere Query Normal approach: Search sphere Faster approach: Search upper hemi-sphere NOTE: will capture each neighbor twice (once from each end) i j

Smaller Optimization Tricks Early elimination if distance between atoms along any dimension > rc. Don’t calculate sqrt: n n Lennard-Jones can be done using dist 2 NOTE: if (dist 2 <= cutoff. Radius 2) is in range Determine optimal # of cells per size. n Is cell length = cutoff radius optimal? j i

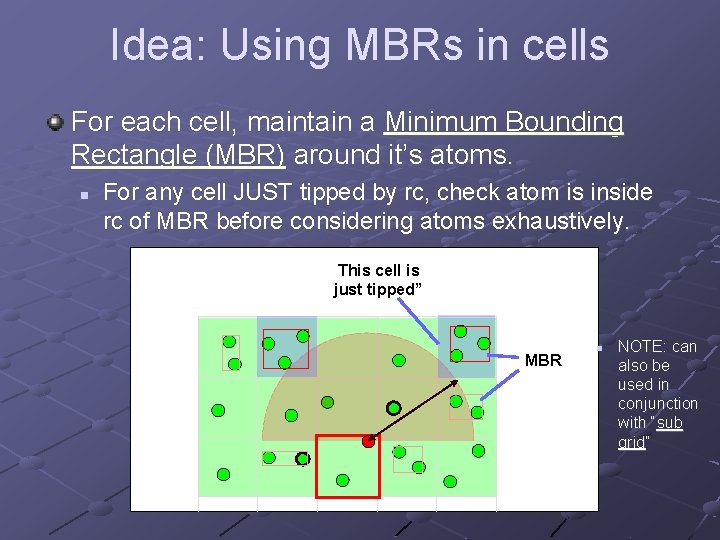
Idea: Using MBRs in cells For each cell, maintain a Minimum Bounding Rectangle (MBR) around it’s atoms. n For any cell JUST tipped by rc, check atom is inside rc of MBR before considering atoms exhaustively. This cell is just tipped” MBR n NOTE: can also be used in conjunction with “sub grid”

Improving Cache Hits through Spatial Locality Spatial locality principle: objects close to referred ones will probably be requested again in the future. n Unsorted atoms means many cache misses. 4 5 3 2 1 6

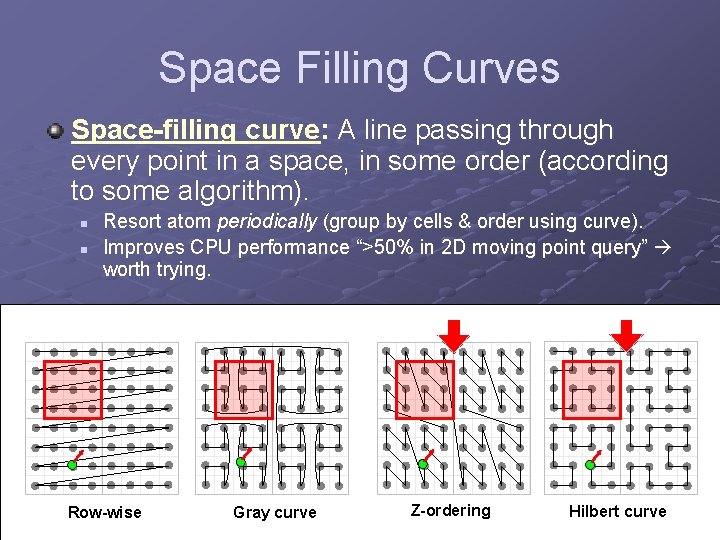
Space Filling Curves Space-filling curve: A line passing through every point in a space, in some order (according to some algorithm). n n Resort atom periodically (group by cells & order using curve). Improves CPU performance “>50% in 2 D moving point query” worth trying. Row-wise Gray curve Z-ordering Hilbert curve

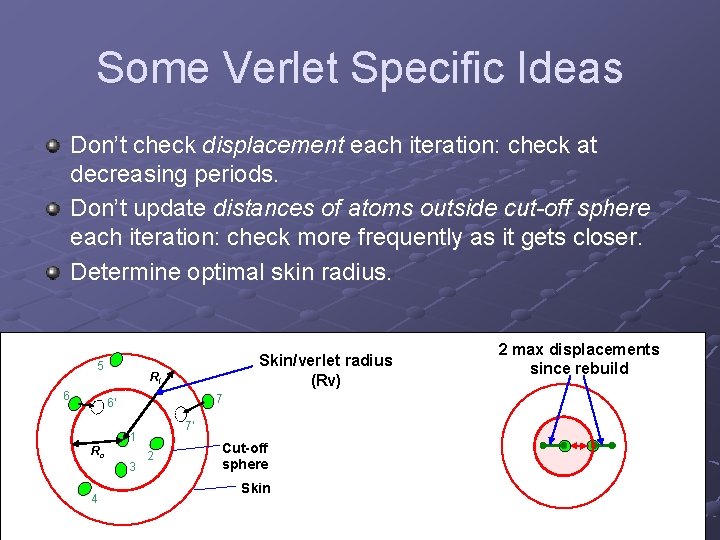
Verlet Neighbour List Choose a “skin radius” greater than rc. Build the “verlet neighbor list” using skin radius Next few iterations: update list; check which neighbour pairs are inside rc. Refinement: only rebuild list when: sum of 2 max displacement (of any 2 atoms) > skin “thickness”. 5 6 Skin/verlet radius (Rv) Rl 7 6' 7' 1 Rc 3 4 2 Cut-off sphere Skin 2 max displacements since rebuild

Some Verlet Specific Ideas Don’t check displacement each iteration: check at decreasing periods. Don’t update distances of atoms outside cut-off sphere each iteration: check more frequently as it gets closer. Determine optimal skin radius. 5 6 Skin/verlet radius (Rv) Rl 7 6' 7' 1 Rc 3 4 2 Cut-off sphere Skin 2 max displacements since rebuild

Performance vs. Accuracy Some techniques that will improve performance, but decrease “accuracy”: n n n Don’t always rebuild/update neighbor list when necessary. small timestep larger timestep Increasing timestep Decreasing cutoff radius I can graph these by testing against a control. large rc smaller rc

Progress Basic grid is implemented Thesis started. Several graphs obtained. Added front end: n n Uses MFC (Microsoft Foundation Class) using Open. GL. Demonstrates building on engine layer. Lets me see particles animate (& work out problems) Code messy Is still MUCH to implement & test.

Conclusion Molecular dynamics : an (approximated) simulation of real world particle behaviour. n Periodic Bounding Condition used for “bulk” liquid 6 Rl 6' 7' 1 Rc rc 2 3 Best existing approach: n 4 5 Verlet list, using cell list & fixed grid to build. Ideas for improvement: n n n Minimal half cell list templates. MBRs inside cells. Space filling curves. Thesis may resemble a guide to implementing/optimizing moving spatial join queries. Still much to be done.

Thank You… Any Questions?

EXTRA SLIDE Revised Goal Implement engine as efficient as possible. How it should work: n Pass in minimum parameters: # atoms, offset, max velocity & box size (or load atom data from file). cutoff radius n Engine should set remaining details to optimal. Including: cells per side, verlet radius, subgrid? mbr? algorithm? etc. rc

EXTRA SLIDE Idea: Sub Grid “Sub grid adjacency list template guide”: break each cell into (imaginary) sub-grid. n When considering an atom, check with sub-cell it belongs to, that sub-cell will refine which adjacent cells to search. NOTE: n n n My primary focus is: reducing time per iteration… but main memory requirements (& setup time) also important. Choosing cell length equal to rc is typical. But is it optimal? No one method/metric is likely to be optimal in ALL cases too many parameters.