Semidefinite Programming Based Approximation Algorithms Uri Zwick Tel

Semidefinite Programming Based Approximation Algorithms Uri Zwick Tel Aviv University UKCRC’ 02, Warwick University, May 3, 2002.

Outline of talk Semidefinite programming MAX CUT (Goemans, Williamson ’ 95) MAX 2 -SAT and MAX DI-CUT (FG’ 95, MM’ 01, LLZ’ 02) MAX 3 -SAT (Karloff, Zwick ’ 97) -function (Lovász ’ 79) MAX k-CUT (Frieze, Jerrum ’ 95) Colouring k-colourable graphs (Karger, Motwani, Sudan ’ 95)

Positive Semidefinite Matrices A symmetric n n matrix A is PSD iff: • x. TAx 0 , for every x Rn. • A=BTB , for some m n matrix B. • All the eigenvalues of A are non-negative. Notation: A 0 iff A is PSD

Linear Programming Semidefinite Programming max c x s. t. ai x bi x 0 max C X s. t. Ai X bi X 0 Can be solved exactly in polynomial time Can be solved almost exactly in polynomial time

LP/SDP algorithms • Simplex method (LP only) • Ellipsoid method • Interior point methods Algorithms work well in practice, not only in theory!

Semidefinite Programming (Equivalent formulation) max cij (vi vj) (k) s. t. aij (vi vj) b vi Rn X ≥ 0 iff X=BTB. If B = [v 1 v 2 … vn] then xij = vi · vj.

Lovász’s -function (one of many formulations) max J X s. t. xij = 0 , (i, j) E I X = 1 X 0 Orthogonal representation of a graph: vi vj = 0 , whenever (i, j) E

The Sandwich Theorem (Grötschel-Lovász-Schrijver ’ 81) Size of max clique Chromatic number

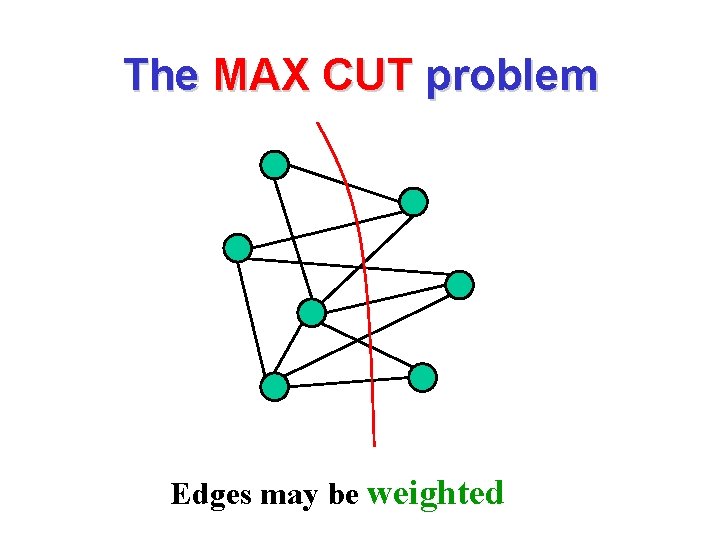
The MAX CUT problem Edges may be weighted

The MAX CUT problem: motivation Given: n activities, m persons. Each activity can be scheduled either in the morning or in the afternoon. Each person interested in two activities. Task: schedule the activities to maximize the number of persons that can enjoy both activities. If exactly n/2 of the activities have to be held in the morning, we get MAX BISECTION.

The MAX CUT problem: status • Problem is NP-hard • Problem is APX-hard (no PTAS unless P=NP) • Best approximation ratio known, without SDP, is only ½. (Choose a random cut…) • With SDP, an approximation ratio of 0. 878 can be obtained! (Goemans-Williamson ’ 95) • Getting an approximation ratio of 0. 942 is NP-hard! (PCP theorem, …, Håstad’ 97)

A quadratic integer programming formulation of MAX CUT

An SDP Relaxation of MAX CUT (Goemans-Williamson ’ 95)

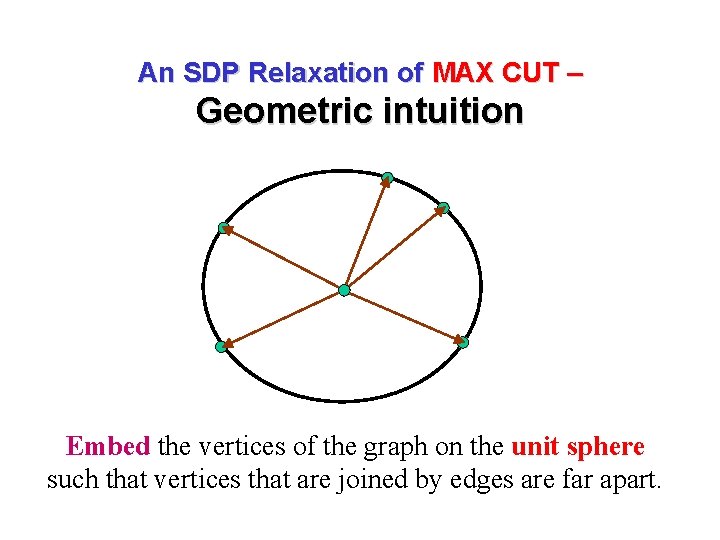
An SDP Relaxation of MAX CUT – Geometric intuition Embed the vertices of the graph on the unit sphere such that vertices that are joined by edges are far apart.

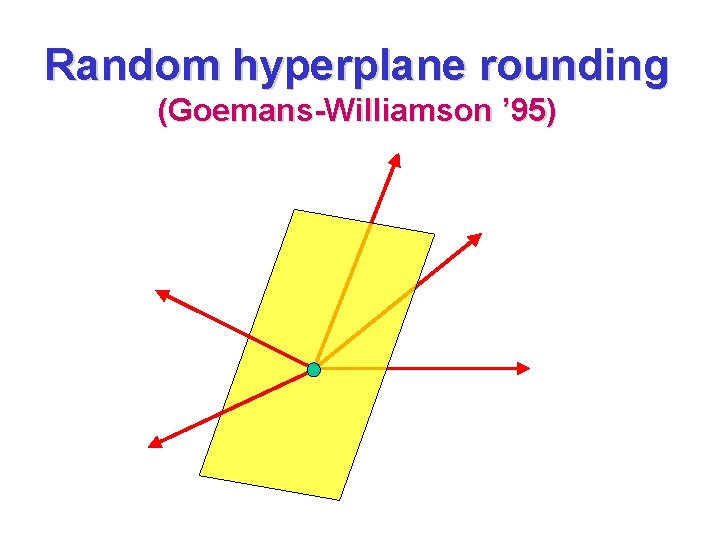
Random hyperplane rounding (Goemans-Williamson ’ 95)

To choose a random hyperplane, choose a random normal vector r If r = (r 1 , r 2 , …, rn), and r 1, r 2 , … , rn N(0, 1), then the direction of r is uniformly distributed over the n-dimensional unit sphere.

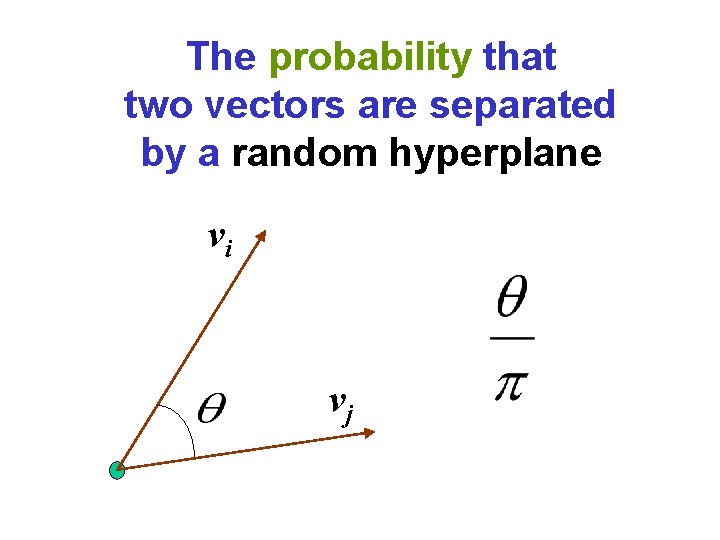
The probability that two vectors are separated by a random hyperplane vi vj

Analysis of the MAX CUT Algorithm (Goemans-Williamson ’ 95)

Is the analysis tight? Yes! (Karloff ’ 96) (Feige-Schechtman ’ 00)

The MAX Directed-CUT problem Edges may be weighted

The MAX 2 -SAT problem

A Semidefinite Programming Relaxation of MAX 2 -SAT (Feige-Lovász ’ 92, Feige-Goemans ’ 95) Triangle constraints

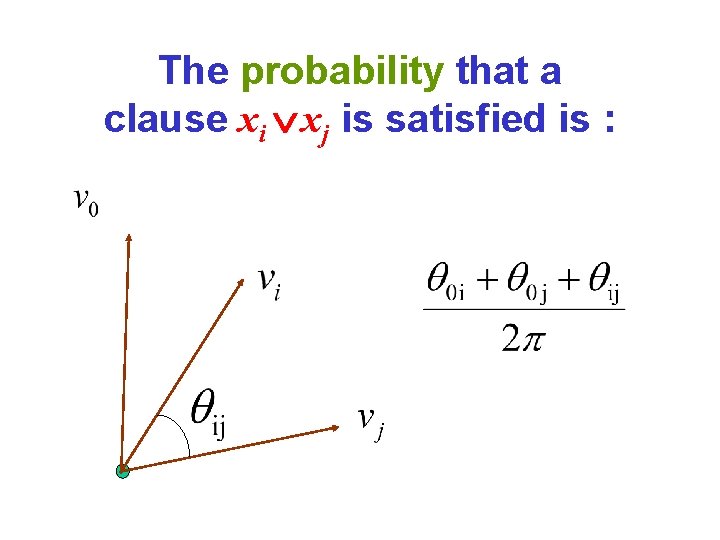
The probability that a clause xi xj is satisfied is :

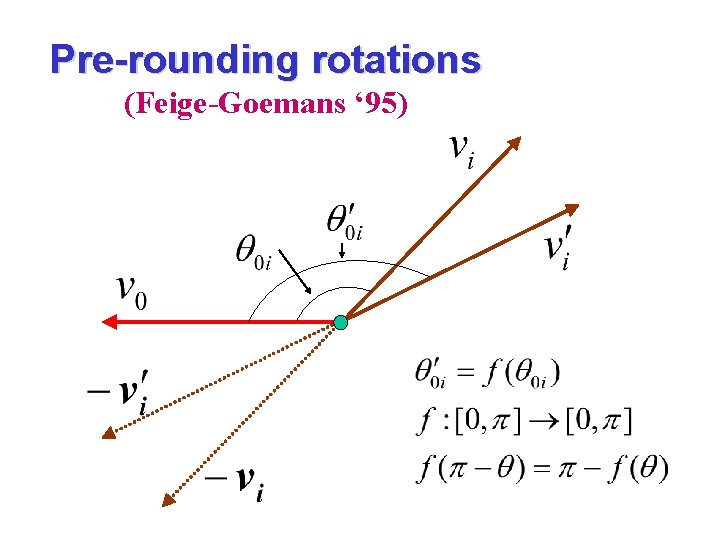
Pre-rounding rotations (Feige-Goemans ‘ 95)

Skewed hyperplanes (Feige-Goemans ’ 95, Matuura-Matsui ’ 01) Choose a random vector r that is skewed toward v 0. Without loss of generality v 0 = (1, 0, …, 0). Let r = (r 1 , r 2 , …, rn), where r 2 , …, rn ~ N(0, 1). Choose r 1 according to a different distribution.

“Threshold” rounding (Lewin-Livnat-Zwick ’ 02) Choose a random vector r perpendicular to v 0. Set xi=1 iff vi · r ≥ T( v 0· vi ).

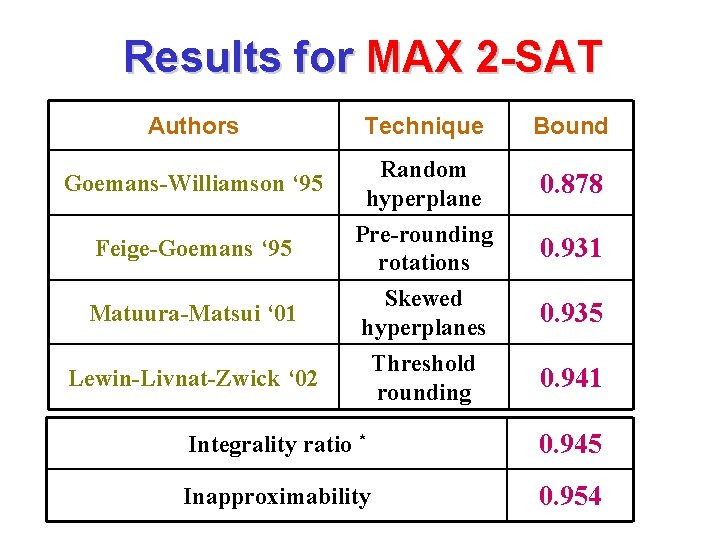
Results for MAX 2 -SAT Authors Technique Bound Goemans-Williamson ‘ 95 Random hyperplane 0. 878 Feige-Goemans ‘ 95 Pre-rounding rotations 0. 931 Matuura-Matsui ‘ 01 Lewin-Livnat-Zwick ‘ 02 Skewed hyperplanes Threshold rounding 0. 935 0. 941 Integrality ratio * 0. 945 Inapproximability 0. 954

The MAX 3 -SAT problem (Karloff-Zwick ’ 97 Zwick ’ 02) A performance ratio of 7/8 is obtained using: § § A more complicated SDP relaxation The simple random hyperplane rounding. A much more complicated analysis. Computer assisted proof. (Z’ 02)

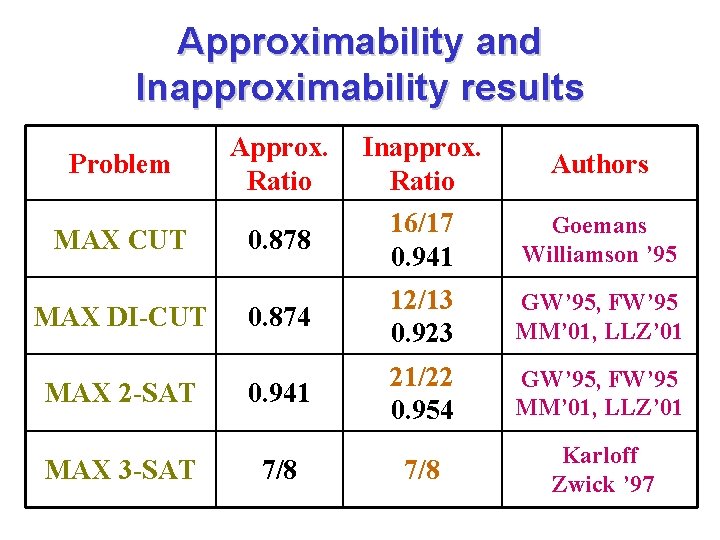
Approximability and Inapproximability results Problem MAX CUT MAX DI-CUT MAX 2 -SAT MAX 3 -SAT Approx. Ratio Inapprox. Ratio Authors 0. 878 16/17 0. 941 Goemans Williamson ’ 95 0. 874 12/13 0. 923 GW’ 95, FW’ 95 MM’ 01, LLZ’ 01 0. 941 21/22 0. 954 GW’ 95, FW’ 95 MM’ 01, LLZ’ 01 7/8 Karloff Zwick ’ 97 7/8

What else can we do with SDPs? • MAX BISECTION (Frieze-Jerrum ’ 95) • MAX k-CUT (Frieze-Jerrum ’ 95) • (Approximate) Graph colouring (Karger-Motwani-Sudan’ 95)

(Approximate) Graph colouring • Given a 3 -colourable graph, colour it, in polynomial time, using as few colours as possible. • Colouring using 4 colours is still NP-hard. (Khanna-Linial-Safra’ 93 Khanna-Guruswami’ 01) • A simple combinatorial algorithm can colour, in polynomial time, using about n 1/2 colours. (Wigderson’ 81) • Using SDP, can colour (in poly. time) using n 1/4 colours (KMS’ 95), or even n 3/14 colours (BK’ 97).

Vector k-Coloring (Karger-Motwani-Sudan ’ 95) A vector k-coloring of a graph G = (V, E) is a sequence of unit vectors v 1 , v 2 , … , vn such that if (i, j) E then vi · vj = -1/(k-1). The minimum k for which G is vector k-colorable is A vector k-coloring, if one exists, can be found using SDP.

Lemma: If G = (V, E) is k-colorable, then it is also vector k-colorable. Proof: There are k vectors v 1 , v 2 , … , vk such that vi · vj = -1/(k-1), for i ≠ j. k=3:

Finding large independent sets (Karger-Motwani-Sudan ’ 95) Let r be a random normally distributed vector in Rn. Let. I’ is obtained from I by removing a vertex from each edge of I.

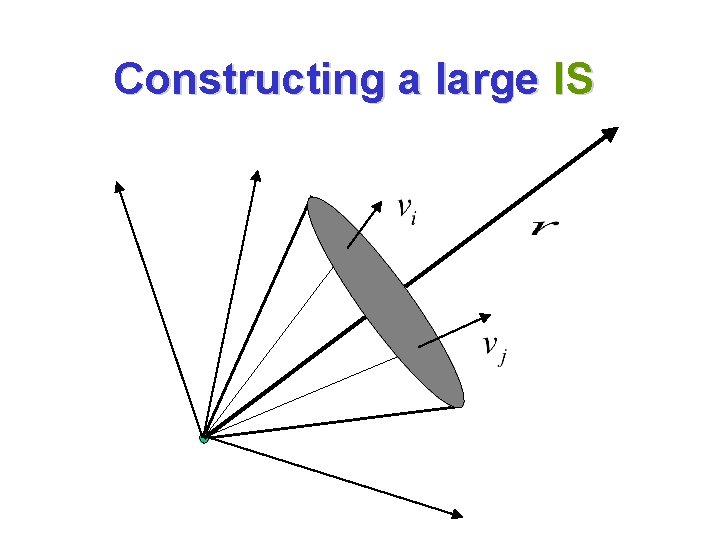
Constructing a large IS

Colouring k-colourable graphs using min{ Δ 1 -2/k , n 1 -3/(k+1) } colours. (Karger-Motwani-Sudan ’ 95) Colouring 3 -colourable graphs using n 3/14 colours. (Blum-Karger ’ 97) Colouring 4 -colourable graphs using n 7/19 colours. (Halperin-Nathaniel-Zwick ’ 01)

Open problems • Improved results for the problems considered. • Further applications of SDP.