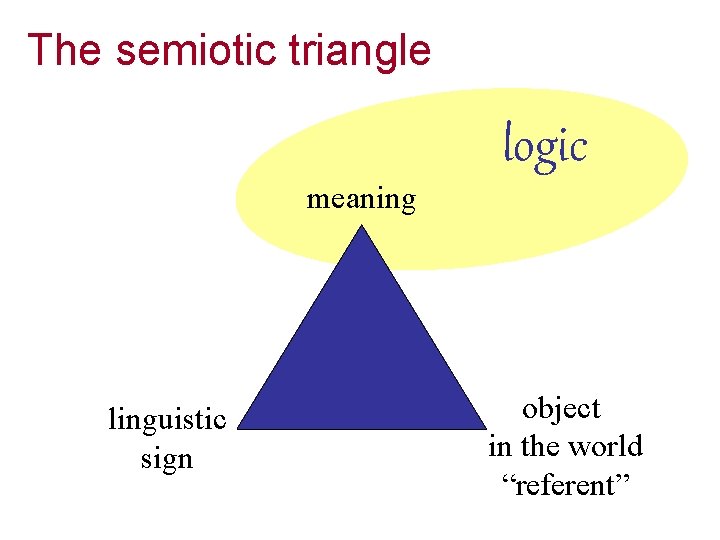
Semantics Logic and Semantics The semiotic triangle logic










- Slides: 15

Semantics Logic and Semantics

The semiotic triangle logic meaning linguistic sign object in the world “referent”

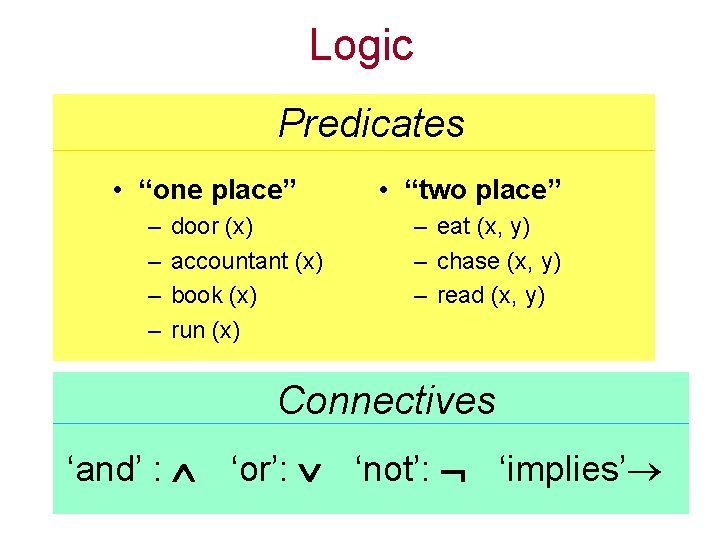
Logic Predicates • “one place” – – door (x) accountant (x) book (x) run (x) • “two place” – eat (x, y) – chase (x, y) – read (x, y) Connectives ‘and’ : ‘or’: ‘not’: ‘implies’

Logical formulae • “If someone chases someone else then both people run” what predicates? what connectives?

Logical formulae • “If someone chases someone else then both people run” chase (x, y) run (x) run (y) person (x) person (y) chase (x, y) run (x) run (y)

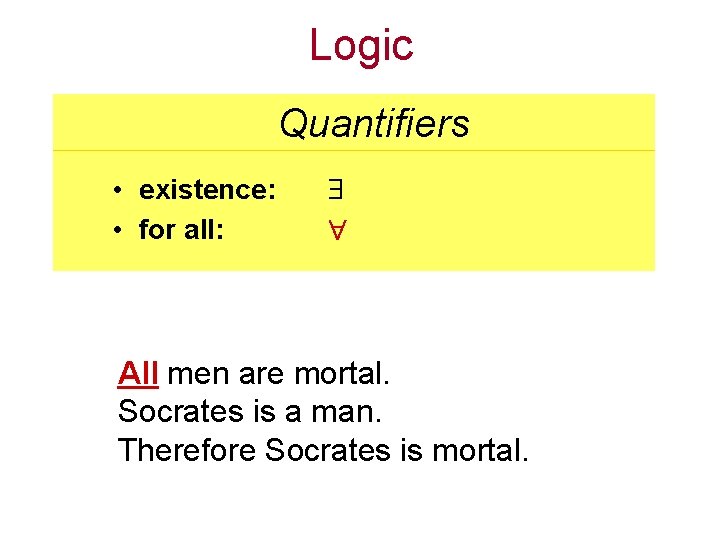
Logic Quantifiers • existence: • for all: All men are mortal. Socrates is a man. Therefore Socrates is mortal.

Logic Quantifiers • existence: • for all: All men are mortal. Socrates is a man. Therefore Socrates is mortal.

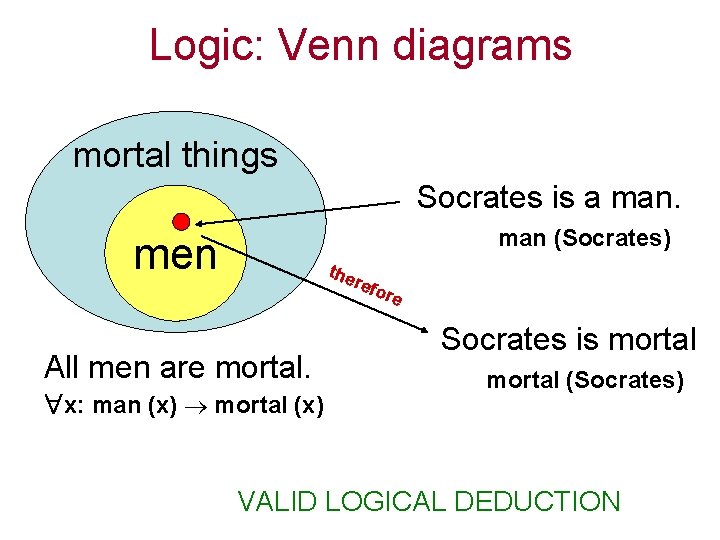
Logic Quantifiers • existence: • for all: All men are mortal. • x: man (x) mortal (x) Socrates is a man. • man (Socrates) Therefore Socrates is mortal (Socrates)

Logic Quantifiers • existence: • for all: All men are mortal. • x: man (x) mortal (x) Some man is mortal. • x: man (x) mortal (x)

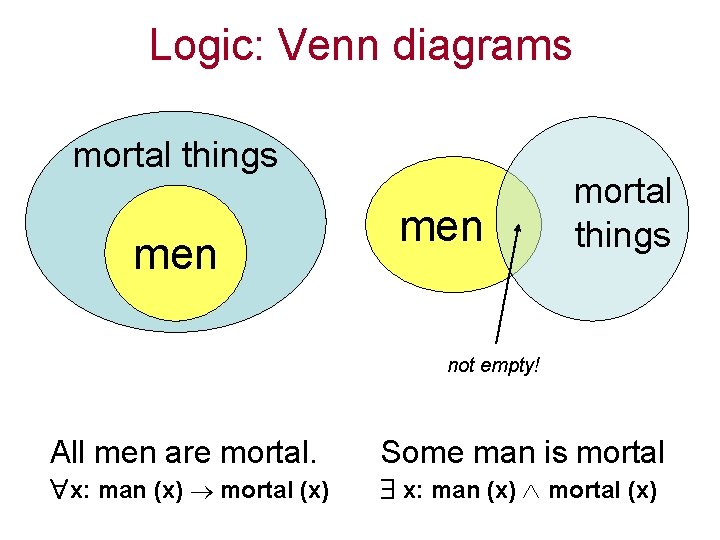
Logic: Venn diagrams mortal things men mortal things not empty! All men are mortal. x: man (x) mortal (x) Some man is mortal x: man (x) mortal (x)

Logical Scope Quantifiers • existence: • for all: All men like some mountain. • x: man (x) like (x, y) • • mountain (y) y: mountain (y) ( x: man (x) like (x, y)) • x: man (x) ( y: mountain (y) like (x, y))

Logical Scope All men like some mountain. higher scope • y: mountain (y) ( x: man (x) like (x, y)) lower scope • x: man (x) ( y: mountain (y) like (x, y))

Logic: Venn diagrams mortal things Socrates is a man (Socrates) men the refo All men are mortal. x: man (x) mortal (x) re Socrates is mortal (Socrates) VALID LOGICAL DEDUCTION

Componential Meanings for verbs… • Dowty… – The door is open. – The door opens. – John opened the door. open(x) become(open(x)) cause(John, become(open(x))) –Statives, inchoatives, causatives…

Logic: capturing ambiguity 1. Every person in this room speaks two languages. 2. Two languages are spoken by everyone in this room. what predicates? what connectives? what quantifiers?