Semantics Describing the meanings of Programs n n

Semantics

Describing the meanings of Programs: n n n Programmers need to know precisely what the statements of a language do. English explanations in language manuals are often imprecise and incomplete. Semantics formalisms are needed by programmers and compiler writers.

Operational Semantics n Describe the meaning of a program by executing its statements on a machine (real or virtual) n The changes that occur in the machine’s state when it executes a given statement define the meaning of that statement. Imagine a machine: n It represents a change in the machine state n

Describing the operational semantics of high-level language statements requires the construction of a real or abstract (virtual) computer. n Example: n The hardware of a computer is a pure interpreter for its machine language Example: n load x architecture

A pure interpreter for a programming language can be constructed in software. (The interpreter is a virtual computer) n Problems with this approach: 1. Complexities of the hardware and operating system will make the interpreter difficult to understand. 2. The semantic definition done this way would be available only for those with an identically configured computer. (machine dependent) n A better alternative is to make a complete computer simulation. n n n The process: Build a translator To translate source code to the machine code of an idealized computer Build a simulator for the idealized computer.

This approach describes the meaning of high-level language statements in terms of statements in a simpler, lower-level language. Example C statement: for ( expr 1; expr 2; expr 3 ) { ---} Operational semantics: expr 1; loop: if expr 2 == 0 goto out --expr 3; goto loop out- - - for ( i = 0; I < 50; ++i ) { ---}

n n n The first and most significant use of formal operational semantics was to describe the semantics of PL/1 (Wegner, 1972). That particular abstract machine and the translation rules for PL/1 were together named the Vienna Definition Language (VDL), after the city where IBM devised it. Operational semantics depends on programming languages of lower levels, not mathematics

Axiomatic Semantics n n It was defined in conjunction with the development of a method to prove the correctness of programs. Such correctness proofs, when they can be constructed, show that a program performs the computation described by its specification.

Axiomatic Semantics is: n n n Based on formal logic (predicate calculus) Original purpose: formal program verification Axioms or inference rules are defined for each statement type in the language

Axioms / Inference Rules n n n This allows for transformations of expressions to other expressions The expressions are called “assertions” In a proof, each statement of a program is both preceded and followed by a logical expression. These logical expressions, rather than the entire state of the abstract machine (operational semantics), are used to specify the meaning of the statement. An assertion before a statement is called a precondition; {P} A precondition states the relationships and constraints among variables that are true at that point of execution An assertion following a statement is called a post condition; {Q} {P} statement {Q}

Note: We assume all variables are integer type Examples Assignment statement 1. {k = 5} k k + 1 {k = 6} 2. {j = 3 k = 4} j j + k {j = 7 k = 4} 3. {a > 0} a a – 1 {a 0}

n n For these examples, correctness is easy to prove either proceeding from the precondition to the post condition or from the post condition to the precondition. Many times starting with the post condition and working backwards to derive the precondition proves easier.

Example 1 n n n {k = 6} post condition {k + 1 = 6} substituting k + 1 for k in post condition {k = 5} precondition, after simplification

Example 2 n n n {j = 7 and k = 4} post condition {j + k = 7 and k = 4} substituting j + k for j in post condition {j = 3 and k = 4} precondition, after simplification.

Example 3 n n {a 0} post condition {a – 1 0} substituting a – 1 for a in post condition {a 1} simplification {a > 0} precondition, since a 1 a > 0 assuming a is an integer

In {PRE} C {POST} The meaning of the command C can be viewed as the order pair <PRE, POST>, called a specification of C n We say that the command C is correct with respect to the specification, if: n n n The precondition is true The command halts And the resulting values make the post condition true. *Extending this notation to an entire program supplies a meaning of program correctness and a semantics to programs in a language.

A Weakest Precondition is the least restrictive one that will guarantee the postcondition Example {b > 10} a b+1 {a > 1} WP {b > 0} a b+1 {a > 1}

Definition n n A program is partially correct with respect to a precondition and a post condition provided that if the program is started with values that make the precondition true, the resulting values make the post condition true when the program halts (if ever). Partial Correctness = (precondition termination post condition)

Definition n n If it can also be shown that the program terminates when started with values satisfying the precondition, the program is called (totally) correct. Total Correctness = (partial correctness termination)

Axioms and Rules of Inference Given an assignment of the form: V = E and a post condition Q, we use the notation: P = [E / V] or P = Q[V E] or P = QV E to indicate the substitution of E in place of each free occurrence of V in Q This notation enables us to give an axiomatic definition for the assignment command. {Q[V E]} V = E {Q}

Example {a > 0} a=a– 1 {a 0} Proof of correctness {a > 0} {a 1} {a – 1 0} = {Q(a – 1)} a=a– 1 {a 0} = {Q(a)}

Example Compute the weakest precondition of the following statement and post condition: x=2*y– 3 {x > 25} {2 * y – 3 > 25} {2 * y > 28} {y > 14} WP

Note: n n A given assignment statement with both a precondition and a post condition can be considered a theorem. We could say that proving the correctness of a program is like proving a theorem.

Rules of Inference n For axiomatic specifications, we introduce rules of inference that have the form:

Interpretation of the notation If S 1, S 2, …, Sn have all been verified, we may conclude that S is valid. Example The sequencing of two commands {P 1} S 1 {P 2} S 2 {P 3}

Example: (Find the WP) y = 3 * x + 1; x = y + 3; {x < 10} y = 3 * x + 1; {y < 7} x = y + 3; {x < 10} {3 * x + 1 < 7} {3 * x < 6} {y + 3 < 10} WP { x < 2} {y < 7} WP {x < 2} y = 3 * x + 1; {y < 7} x=y+3 {x < 10}

The IF command ( IF – THEN – ELSE ) n n The if command involves a choice between alternatives. Note that the Boolean expression B is used as part of the assertion in the premises of the rule.

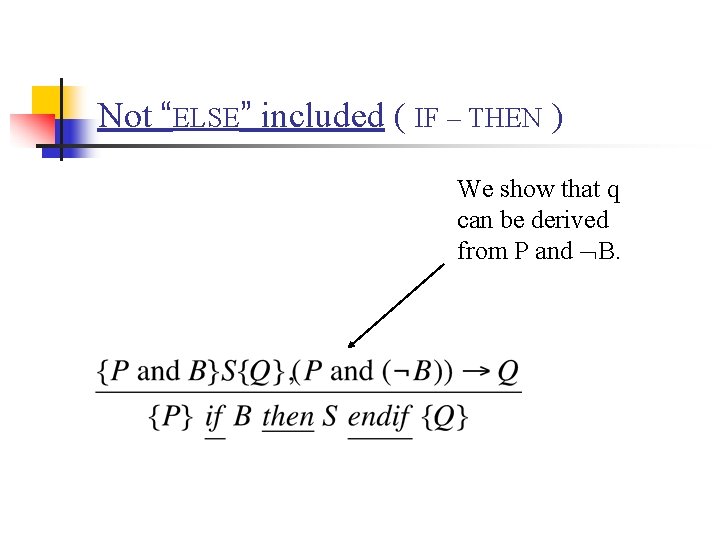
Not “ELSE” included ( IF – THEN ) We show that q can be derived from P and B.

Example if (x > 0) y=y– 1 else y=y+1 {y > 0}

1) We use the axiom in the first assignment statement y=y– 1 {y > 0} 2) Second assignment statement. y=y+1 {y > 0} {y – 1 > 0} {y + 1 > 0} {y > 1} {y > – 1} { y > 1} {y > – 1} The rule of consequence allows us to use {y > 1} as the precondition of the whole statement.

While command the Loop Invariant n In this definition P is called the Loop Invariant.

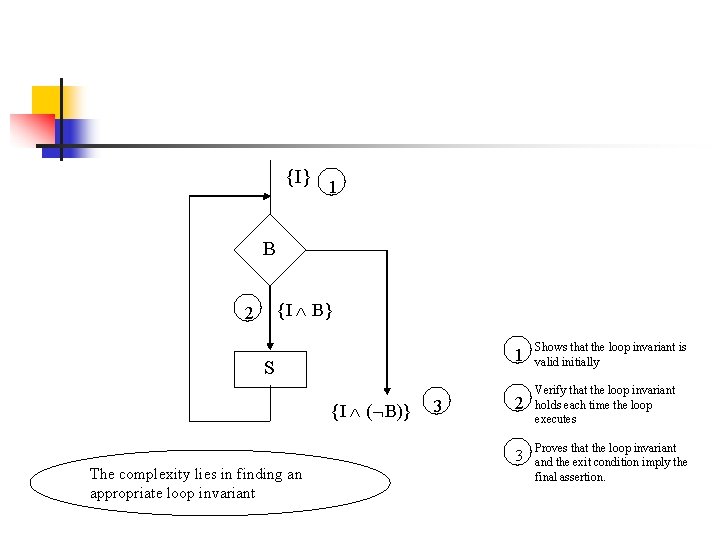
{I} 1 B {I B} 2 S {I ( B)} The complexity lies in finding an appropriate loop invariant 3 1 Shows that the loop invariant is valid initially 2 Verify that the loop invariant holds each time the loop executes 3 Proves that the loop invariant and the exit condition imply the final assertion.

n n As we have called P the invariant, let us rewrite the while axiom as: Where I is the loop invariant

The complete axiomatic description of a while construct requires all of the following to be true, in which I is the loop invariant: 1) P I, the weakest precondition for the while statement must guarantee the truth of I. 2) {I and B}S{I}, the statement does not affect the loop invariant. 3) (I and (not B)) Q, the loop invariant implies the post condition at termination. 4) The loop terminates (In general, this may be very difficult to prove).

n To find the loop invariant, we can use a method similar to that used for determining the inductive hypothesis in mathematical induction: n n “The relationship for a few cases is computed, with the hope that a pattern emerges that will apply to the general case. ” It is useful to treat the process of producing a WP as a function: n WP(statement, post condition) = precondition

Example while (y <> x) do y : = y + 1 endwhile {y = x}

Step 1: Find the invariant (I)

It is obvious that: {y < x} will suffice for cases of one or more iterations.

Combining {y < x} with {y = x} for 0 iterations, we get I = {y x} the loop invariant 1. P = I, P I 2. {I and B}S{I} {y x and y < > x}y = y + 1{y x} I B we compute the WP. WP(y : = y + 1, {y x}) = {y + 1 x} {y < x} and {y x and y < >x} { y < x} which proves the assertion {y < x} is implied by {y x and y < > x}

3. {(I and not(B)} Q ? {(y x) and not(y <> x)} {y = x} {(y x) and (y = x)} {y = x}, so proven. 4. The loop terminates? Since x and y are integers and {P} = {I} states that {y x}, and the loop body increases y with each iteration until y is equal to x, it will eventually terminate.

n To define the entire semantics of a programming language using axiomatic methods, there must be an axiom or an inference rule for each statement type in the language.

Axiomatic Semantics is a powerful tool for research into program correctness proofs. n n It provides an excellent framework in which to reason about programs It has limited usefulness for either compiler writers or language users.

Denotational Semantics is the most rigorous, widely-known method for describing the meaning of programs. n n n Based on recursive function theory The most abstract semantics description method Originally developed by Scott and Strachey (1970) We can predict the behavior of each program without actually executing it on a compiler Denotational Semantics assigns a meaning not only to a complete program, but also to every phrase in the programming language n n Every expression Every command Every declaration Etc.

n n n The meaning of each phrase is called a denotation and it represents a mathematical entity. (A denotation of the phrase) We specify the programming language’s semantics by functions that map phrases to their denotations. These functions are called: Semantic functions

Example n n Consider a language of binary numerals, such as ‘ 110’ and ‘ 10101’. The numeral ‘ 110’ is intended to denote the number six and ‘ 10101’ denotes twenty-one. It is important to understand that a numeral is a syntactic entity, whereas a number is a semantic entity. A number is an abstract concept, not dependent on any particular syntactic representation.

Example of number as an abstract concept n The natural number six is n n n denoted by ‘ 101’ in the language of binary numerals, denoted by ‘ 6’ in the language of decimal numerals, denoted by ‘VI’ in the language of Roman numerals.

n Traditionally, denotational definitions use special brackets: The emphatic brackets to separate the syntactic world from the semantic world.

n For instance, if P is a syntactic phrase in a programming language, then the denotational specification of the language will define a mapping meaning so that meaning P is the denotation of P An abstract mathematical entity that models the semantic of P.

Example n n n The expressions “ 2 * 4”, “(5 + 3)”, “ 008”, and “ 8” are syntactic phrases that all denote the same abstract object, namely the integer 8. The denotational definition is meaning 2*4 008 = meaning (5 + 3) = 8 =8

n sometimes we call it valuation instead of meaning 2*4 valuation 2*4 =8

Example n n Syntax of binary numerals NUMERAL : : = 0 | 1 | NUMERAL 0 | NUMERAL 1 each numeral denotes a natural number in the following domain (semantic domain) NATURAL = {0, 1, 2, 3, …}

Semantic Function n meaning : numeral natural map each numeral to the natural number it denotes

We can define a new meaning by four equations (semantic equations) n valuation or meaning 0 =0 n meaning 1 =1 n meaning N 0 = 2 * meaning N n meaning N 1 = 2 * meaning N +1

Now we can use the semantic equations to determine the denotations of any binary numeral in our little tiny language. n meaning 110 = 2 * (2 * meaning = 2 * (2 * 1 + 1) = 2 * (2 + 1) =2*3 =6 = 2 * meaning 1 + 1) 11

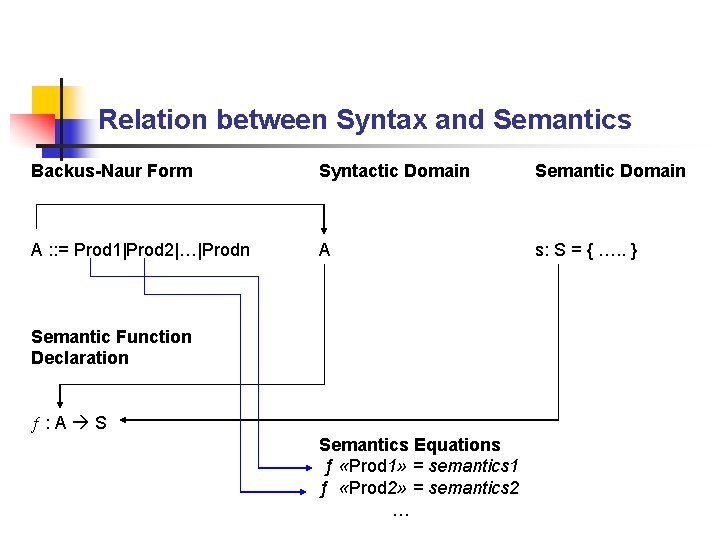
Relation between Syntax and Semantics Backus-Naur Form Syntactic Domain Semantic Domain A : : = Prod 1|Prod 2|…|Prodn A s: S = { …. . } Semantic Function Declaration ƒ: A S Semantics Equations ƒ «Prod 1» = semantics 1 ƒ «Prod 2» = semantics 2 …

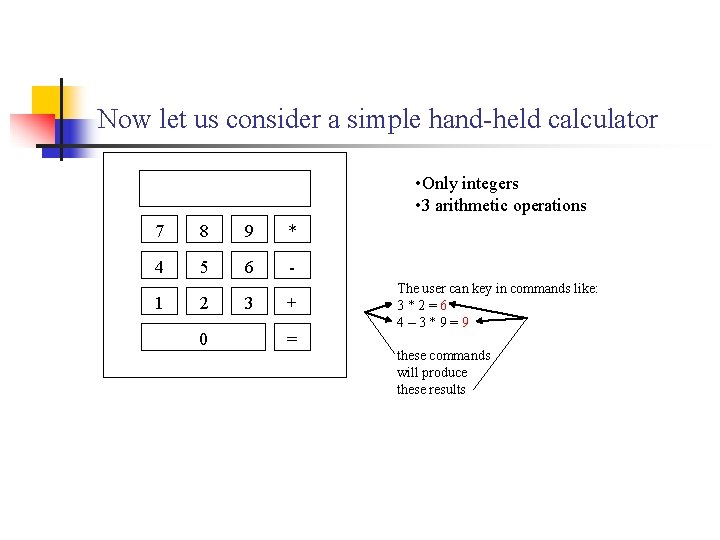
Now let us consider a simple hand-held calculator • Only integers • 3 arithmetic operations 7 8 9 * 4 5 6 - 1 2 0 3 + = The user can key in commands like: 3*2=6 4– 3*9=9 these commands will produce these results

Syntax of the Calculator Language We can identify four phrase classes n n commands ‘ 3 * 9 = ’, ‘ 40 – 3 * 9 = ’ EXPR expressions ‘ 3 * 9’, ‘ 40 – 3 * 9’ NUM numerals ‘ 3’, ‘ 9’, ‘ 40’ DIG digits (‘ 0’, ‘ 1’, ‘ 2’, …, ‘ 9’) COM we call COM, EXPR, NUM, and DIG non-terminal symbols. n COM will be the start symbol

Production Rules n n COM : : = EXPR : : = NUM | EXPR + NUM | EXPR – NUM | EXPR * NUM : : = DIG | NUM DIG : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Syntax Trees The sentence or command COM EXPR EXPR NUM NUM 40 – 3 * 9 =

Let us define the semantics of the language CALC (calculator) n Abstract syntax command : : = expression : : = numeral | expression + expression | expression – expression | expression * expression

We need to define CALC on the following domain n Integers = {…, -3, -2, -1, 0, 1, 2, 3, . . . } and the following auxiliary functions n n n sum difference product : integer integer : integer

We will assume that n n sum(i, j) = fail (does not occur!) when CALC commands are executed, the effect is to display its result (an integer) n Let the denotation of each command C be the integer it displays n Each expression E also denotes an integer (its value) n Each numeral N denotes a natural number

We formalize these statements by introducing the concept of semantics functions: n n n execute: command integer evaluate: expression integer valuation: numeral natural As there is only one form of command (‘E = ’) we define the semantic function execute by a single equation. n execute E= = evaluate E

As there are four forms of expression, we need four equations to define the semantic function evaluate: n evaluate E 1+E 2 = sum (evaluate E 1, evaluate E 2) n evaluate E 1+E 2 = difference (evaluate E 1, evaluate E 2) n evaluate E 1+E 2 = product (evaluate E 1, evaluate E 2) n valuation 0 =0 was defined above.

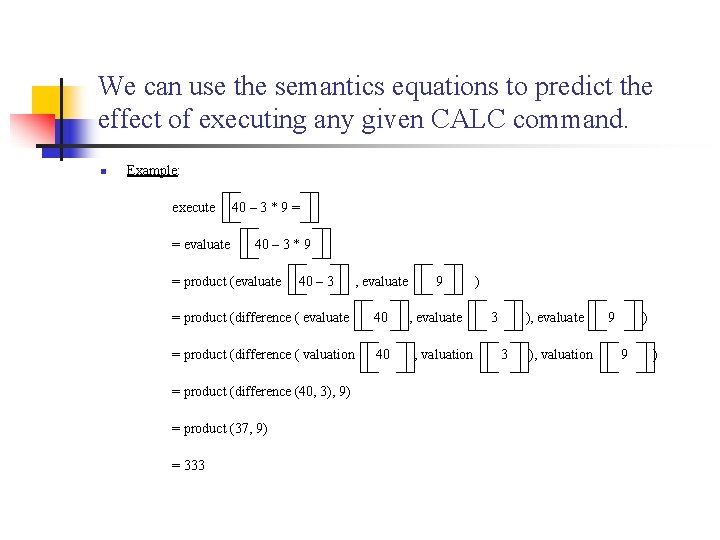
We can use the semantics equations to predict the effect of executing any given CALC command. n Example: execute = evaluate 40 – 3 * 9 = product (evaluate 40 – 3 , evaluate 9 = product (difference ( evaluate 40 , evaluate = product (difference ( valuation 40 = product (difference (40, 3), 9) = product (37, 9) = 333 , valuation ) 3 ), evaluate 3 ), valuation 9 )