Semantica operazionale La semantica ha lo scopo di

Semantica operazionale: • La semantica ha lo scopo di definire il significato di un programma, • la semantica operazionale raggiunge tale scopo definendo il comportamento del sistema (calcolatore) mentre esegue il programma. • Il comportamento del programma viene definito utilizzando un sistema di transizioni in cui – le configurazioni devono permettere di definire lo stato del sistema, – le configurazioni terminali rappresentano i risultati, – le transizioni descrivono l’evoluzione del sistema durante la computazione delle istruzioni del programma. 12/14/2021 1

Un sistema di transizioni per espressioni semplici • Il sistema di transizioni che descrive la semantica di un linguaggio di programmazione (anche se non completo), è piuttosto complesso, per cui verrà introdotto per passi; • Inizieremo con semplice linguaggio di espressioni che può essere descritto da un sistema di transizione molto semplice • via estenderemo il linguaggio, con nuovi meccanismi e di conseguenza il sistema di transizioni verrà anch’esso esteso. Espresioni semplici 12/14/2021 Exp: : = Exp Op Exp | Num | ‘(‘Exp’)’ Op: : = + | - | * | / Num: : =. . . 2

Il sistema di transizioni per le espressioni semplici Semantica di Exp: S < , T , > • {E | E Exp} {n | n } • T {n | n } • (Expop) E exp n E’ exp n’ n [op] n’ = m exp exp E op E’ exp m (Exp()) (Exp. Num) 12/14/2021 E exp n (E) exp n n exp n 3

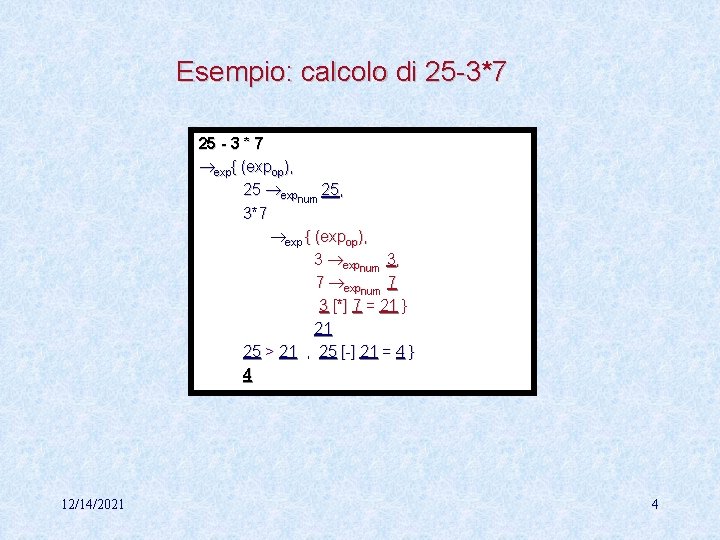
Esempio: calcolo di 25 -3*7 25 - 3 * 7 exp{ (expop), 25 expnum 25, 3*7 exp { (expop), 3 expnum 3, 7 expnum 7 3 [*] 7 = 21 } 21 25 > 21 , 25 [-] 21 = 4 } 4 12/14/2021 4

Semantica Operazionale: Espressioni Ia estensione (identificatori per costanti) • Riferire una quantità mediante un nome è utile ed è prassi comune in molti formalismi. • Le variabili in matematica sono dei nomi (identificatori) ai quali è associato un valore. • Nei linguaggi di programmazione di tipo imperativo (e quindi anche object-oriented come Java) gli identificatori con associato il valore sono un meccanismo fondamentale per la definizione dei programmi. = 138, 16 allorche’ Pigreco=3, 14 2 * Pigrego * 22 = 138, 226 allorche’ Pigreco=3, 1415 12/14/2021 5

Identificatori • In ogni linguaggio è necessario definire dei nomi, nei L. P. i nomi vengono chiamati identificatori ed hanno una particolare sintassi, generalmente: Ide: : =Lettera Carattere* Lettera: : =A|B|C|…|Z|a|b|…|z, Carattere: : =Lettera|Cifra|Simbolo, Cifra: : =0|1|2|…|9, Simbolo: : =-|$|%|: |<|…, Alcuni simboli non sono ammessi 12/14/2021 6

Un linguaggio d’espressioni con identificatori di costanti Una grammatica G Exp: : = Exp Op Exp | Num | ‘(‘ Exp ‘)’ | Ide Op: : = + | - |* | / Num: : = … Ide: : =. . . 12/14/2021 7

Frame • Un frame è una funzione da Identificatori in Valori: Ide Val. • è una funzione parziale cioè definita solo per alcuni valori del dominio per gli altri è indefinita ( ). • w è il frame sempre indefinito (cioè x Ide w(x)= Esempi: se 1={<Pigreco, 3. 14>, <Euro, 1936>} e 2={<Pigreco, 3. 1415>} 1(Pigreco)=3. 14 (2 * Pigrego * 22) 1 = 138, 16 2(Pigreco)=3. 1415 (2 * Pigrego * 22) 2 = 138, 226 1(Euro)= 1936 2(Euro)= 12/14/2021 8

Espressioni con identificatori di costanti Semantica di Exp: S < , T , > • {<E, > | E Exp, {Ide Val} {n | n } • T {n | n } <E, > exp n <E’, > exp n’ n [op 1] n’ = m • (Exp ) exp exp <E op 1 E’, > exp m +|- (Exp()) 12/14/2021 <E, > exp n <(E), > exp n (Exp. Num) <n, > exp n (Exp. Ide) (x)= n <x, > exp n 9

Esempio: calcolo di 2*Pigreco*22 <2 * Pigreco * 22, {Pigreco=3}> exp{ (exp*|/), 2 expnum 2 , Pigreco * 22 exp { (exp*|/), Pigreco exp { (exp. Ide), (Pigreco)=3 } 3 22 expnum 22 3 [*] 22 = 66 } 66 2 [*] 66 = 132 } 132 12/14/2021 10