Semantic networks An alternative knowledge representation framework Semantic

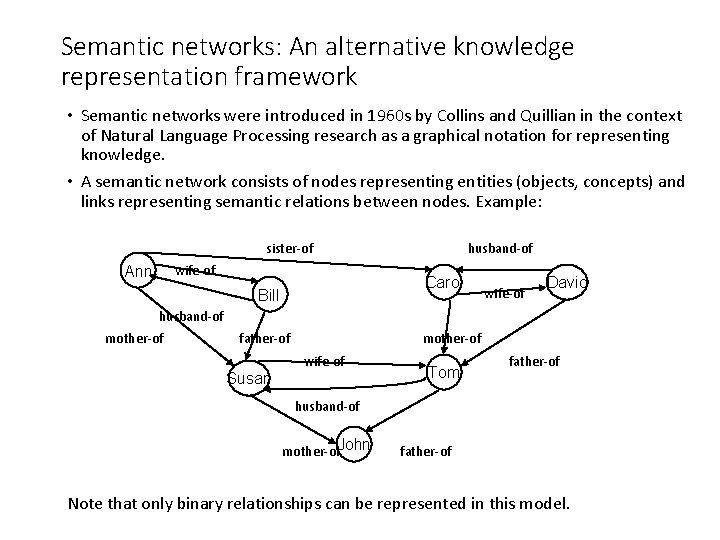
Semantic networks: An alternative knowledge representation framework • Semantic networks were introduced in 1960 s by Collins and Quillian in the context of Natural Language Processing research as a graphical notation for representing knowledge. • A semantic network consists of nodes representing entities (objects, concepts) and links representing semantic relations between nodes. Example: sister-of wife-of Ann husband-of Carol Bill wife-of David husband-of mother-of father-of Susan mother-of wife-of Tom father-of husband-of mother-of. John father-of Note that only binary relationships can be represented in this model.

Foundation of semantic networks Every sentence in NL can be divided into 2 or 3 main components: • the subject (a required component) refers to the origin of the action; • the predicate / relation (a required component) refers to the action itself; • The object (not required) is associated with the predicate and identifies the direction of the action. Examples: Ann IS-A-SISTER-OF Carol. Jones TEACHES Math 101. All these are binary relations consisting of a Zlatareva IS-A Lecturer. subject, a predicate, and an object. A binary predicate/relation, R, between two sets of elements, A and B, is a set of ordered pairs of elements of these two sets. Example: Jones A, Math 101 B, TEACHES R. 2

Domain and Range of a relation • The domain of R is a set of all objects x A, such that x R y. • The range of R is a set of all objects y B, such that x R y. Example: If we consider ALL people who teach as elements of set A, then each one of these people can be substituted for x. If we consider ALL courses as elements of set B, then each one of these courses can be substituted for y. Note that some binary relations can be expressed as equivalent unary relations. Example: Zlatareva IS-A Lecturer, can be represented as Lecturer(Zlatareva). • A unary predicate/relation on a set A is simply a subset of A, i. e. Zlatareva A, where Zlatareva C and C A. • Unary relations are called classes. 3

Description logics (book, page 456) Description logics are decidable fragments of FOL intended to represent categories (classes/concepts), the relations between classes (roles) and individuals. Example: Consider category “Student”. One possible definition of this category is Student And(takes-classes, does-homeworks, is-responsible) Note that this definition can be translated into the following FOL sentence x (Student(x) <=> Takes-classes(x) & Does-homeworks(x) & & Is-responsible(x)) Example: Consider category of men with at least three sons who are all unemployed and married to doctors, and at most two daughters who are all professors in physics or chemistry departments. Man 3 SS 2 SD And(Man, At-Least(3, Son), At-Most(2, Daughter), All(Son, And(Unemployed, Married, All(Spouse, Doctor))), All(Daughter, And(Professor, Fills(Department, Physics, Chemistry)))). DLs is a family of logics which defer by their expressivity depending on the constructors employed to build complex descriptions from simple ones. They are used primarily to describe declarative knowledge.

General Architecture of Description Logics DL knowledge base consists of 3 parts: • The TBox, which contains terminological knowledge, i. e. knowledge about concepts in a domain). Examples: • Student Person ⊓ takes. Course In FOL, x (Student(x) <==> Person(x) & y (takes. Course(x, y) & Course(y))) • Student ⊑ Person In FOL, x (Student(x) Person(x)). • The ABox, which contains assertion knowledge, i. e. knowledge about individuals. Example: Student (Bob), takes. Course (Bob, Computer. Science) • The RBox, which contains role-centric knowledge, i. e. knowledge about interdependences between roles/properties Example: teaches. Grad. Course ⊑ teaches. At. Univ RBox is not required; only more expressive DLs have constructors to handle RBoxes. The smallest deductively complete DL is called ALC (Attributive Language with Complements).

ALC: Syntax § ALC Atomic types: • Concept names: A, B, C, … • Top and bottom concepts, ᴛ and • Role names: R, S, … § ALC Constructors: ⊓, ⊔, , R. C and R. C § Class inclusion and equivalence axioms: ⊑, Example: Student ⊑ Person, Ph. DThesis Dissertation § Complex class relations are built from atomic types and ⊓, ⊔, Example: Instructor ⊑ (Staff ⊓ Professor) ⊔ Lecturer In FOL: x Instructor(x) (Staff(x) Professor(x)) Lecturer(x) § Quantifiers on Roles: • Strict binding of a role to a class. Example: A thesis must be authored by a student, i. e. Thesis ⊑ author. Student In FOL: x (Thesis(x) y(author(x, y) Student(y))) • Open binding of a role to a class. Example: Every student has at least one advisor, i. e. Student ⊑ advisor. Professor In FOL: x (Student(x) y (advisor(x, y) Professor(y)))

ALC: Formal Syntax § Production rules for creating classes in ALC : C, D : : = A | T | | C ⊓ D | C ⊔ D | R. C where A is an atomic class, C and D are complex classes, and R is a role. § An ALC TBox contains assertions of the forms C ⊑ D and C D § An ALC ABox contains assertions of the form C(a) and R(a, b), where a and b are individuals. § An ALC Knowledge Base = {TBox, ABox}.

ALC: Semantics § An interpretation, I = ( I, . I), is defined by: • A domain of individuals, I • An interpretation function. I which maps • Individual names, a, to domain elements a. I I • Class names, C, to a set of domain elements CI I • Role names, R, to a set of pairs of domain elements R I I I § An interpretation, I, for axioms: • C(a) holds iff a. I CI • R(a, b) holds iff (a. I, b. I) RI • C ⊑ D holds iff CI DI • C D holds iff CI = DI § An interpretation, I, for complex classes is defined as follows: • TI = I and I = • (C ⊓ D)I = CI DI , (C ⊔ D)I = CI DI , ( C)I = I CI • R. C = {a I |( b I ) ((a, b) RI b CI )} • R. C = {a I | ( b I ) ((a, b) RI b CI )}

More DL constructors that are beyond ALC § Number restrictions for roles. Example: 20 has. Student § Qualified number restrictions for roles. Example: 6 has. Student. Graduate § Nominals (definition by enumeration): {CS 151, CS 152, CS 253} § Concrete domains (datatypes): has. Student. ( 20) § Inverse roles: has. Child- has. Parent § Transitive roles: has Ancestor ⊑+ has Ancestor § Role composition: has. Parent. has. Brother (uncle) Constructors allowed to define the specific DL. Examples • • • S: ALC + Transitive roles; R: Role constructors; O: Nominals; I: Inverse roles; Q: Qualified number restrictions; (D): datatypes. SROIQ(D) is the DL behind the latest version of OWL 2.

Questions DLs inference must address § Does the knowledge base make sense? § Are there empty classes? § Are two classes equivalent? § Does one class subsume another class? § Are two classes disjoined? § Is a given individual a member of a specified class? § Find all individuals of a given class. The so-called tableaux algorithm (initially developed for FOL) is adapted to DLs to guarantee that these questions are answered in finite time. Tableaux algorithm proves unsatisfiability of a KB using the refutation method and transformation rules similar to Wang’s algorithm (called here tableaux extension rules)

Tableaux algorithm: PL example Given an expression in disjunctive normal form, construct the tableaux / decision tree where each node is a logical formula, each path from the root note to a leaf note is a conjunction of formulas, and each branch of a path is a disjunction of formulas. To build the tree, we apply the following rules: Example: (A & B & C) (D & A) (B & D) -rule (A & B & C) -rule (D & A) (B & D) -rule A (D & A) B D C A (B & D) B D -- -Rules: (A & B) => A, B (A B) => A, B -- -Rules: A A B B A (A & B) B A A B B -- Double negation rule: A => A -- True => False, False => True

Tableaux Algorithm for ALC Step 1: Translate the DL KB to a negation normal form (NNF) using the following transformations: i. Substitute C D by C ⊑ D and D ⊑ C ii. Substitute C ⊑ D by C ⊔ D iii. Apply all possible NNF transformations to complex classes: i. NNF ( C) NNF (C) ii. NNF (C ⊔ D) NNF (C) ⊔ NNF (D) iii. NNF (C ⊓ D) NNF (C) ⊓ NNF (D) iv. NNF ( (C ⊔ D)) NNF ( C) ⊓ NNF ( D) v. NNF ( (C ⊓ D)) NNF ( C) ⊔ NNF ( D) vi. NNF ( R. C) ( R). NNF (C) viii. NNF ( R. C) ( R). NNF ( C) ix. NNF ( R. C) ( R). NNF ( C)

Tableaux Algorithm for ALC (contd. ) Step 2: Apply the following tableaux expansion rules to derive new ABox facts until no more rules can be applied (in which case we say that the tableaux is fully expanded). § ⊓ -Rule if (C ⊓ D) (a) ABox and {C(a), D(a)} ABox, then ABox’ = Abox {C(a), D(a)} § ⊔ -Rule if (C ⊔ D) (a) ABox and {C(a), D(a)} ABox = , then ABox’ = ABox {C(a)} and ABox” = ABox {D(a)} § -Rule if R. C(a) ABox and there is no b such that C(b) ABox and R(a, b) ABox then Abox ‘ = Abox {C(z), R(a, z)} for a new individual z ABox § -Rule if R. C(a) ABox and R(a, b) Abox, but C(b) ABox then Abox ‘ = Abox {C(b)} The algorithm returns TRUE if there is a clash-free tableaux and FALSE if the tableaux is closed. The tableaux is closed if all its paths are closed, where a path is closed if a formula and its negation occur along that path, or if false occurs. To prove X, we must obtain a closed tableaux for X.

Example Let TBox = {Professor ⊑ (Person ⊓ Staff) ⊔ (Person ⊓ Student)} Prove: Professor ⊑ Person Step 1: Negate the conclusion you want to prove. (Professor ⊑ Person) Step 2: Convert all formulas in the NNF: TBox = { Professor ⊔ (Person ⊓ Staff) ⊔ (Person ⊓ Student)} NNF ( (Professor ⊑ Person)) = NNF ( ( Professor ⊔ Person)) = = NNF (Professor) ⊓ NNF ( Person) = Professor ⊓ Person Step 3: Apply the tableaux extension rules to derive new ABox facts from the TBox extended with the negated theorem.

Example: step 3 (contd. ) (1)Professor(a) ⊓ Person(a) (Consider a new individual a for whom you are disproving theorem) (2) Apply ⊓-rule to (1): Professor(a) closed path (3)Apply ⊓-rule to (1): Person(a) closed path (4) Professor(a) ⊔ (Person(a) ⊓ Staff(a)) ⊔ (Person(a) ⊓ Student(a)) (5)Apply ⊔-rule to (4): Professor(a) (6) Apply ⊔-rule to (4): (Person(a) ⊓ Staff(a)) ⊔ (Person(a) ⊓ Student(a)) (7) Apply ⊔-rule to (6): (Person(a) ⊓ Staff(a)) (8) Apply ⊔-rule to (6): (Person(a) ⊓ Student(a)) closed path (9) Apply ⊓-rule to (7): Person(a) (10) Apply ⊓-rule to (7): Staff(a) (11) Apply ⊔-rule to (8): Person(a) (12) Apply ⊔-rule to (8): Student(a) No more rules can be applied – the tableaux is fully expanded and closed. Therefore, the original theorem is proved.

Another example Given the following KB: Woman Person ⊓ Female Man Person ⊓ Woman Mother Woman ⊓ has. Child. Person Father Man ⊓ has. Child. Person Parent Mother ⊔ Father Grandmother Woman ⊓ has. Child. Parent Prove: Grandmother ⊑ Person. 1. Negate the goal and add it to the KB, i. e. add (Grandmother ⊓ Person). 2. Translate the KB into the negation normal form i. ) substitute A B with A ⊑ B and B ⊑ A Woman ⊑ Person ⊓ Female ⊑ Woman Man ⊑ Person ⊓ Woman ⊑ Man Mother ⊑ Woman ⊓ has. Child. Person ⊑ Mother Father ⊑ Man ⊓ has. Child. Person ⊑ Father Parent ⊑ Mother ⊔ Father ⊑ Parent Grandmother ⊑ Woman ⊓ has. Child. Parent ⊑ Grandmother 16

Subsumption example (contd. ) ii. ) substitute A ⊑ B with A ⊔ B and then apply all possible transformations to complex classes to bring negation down to atomic classes: Woman ⊔ (Person ⊓ Female) ⊔ Woman Person ⊔ Female ⊔ Woman Man ⊔ (Person ⊓ Woman) ⊔ Man Person ⊔ Woman ⊔ Man Mother ⊔ (Woman ⊓ has. Child. Person) ⊔ Mother Woman ⊔ has. Child. Person ⊔ Mother Father ⊔ (Man ⊓ has. Child. Person) ⊔ Father Man ⊔ has. Child. Person ⊔ Father Parent ⊔ (Mother ⊔ Father) Parent ⊔ Mother ⊔ Father (Mother ⊔ Father) ⊔ Parent ( Mother ⊓ Father) ⊔ Parent Grandmother ⊔ (Woman ⊓ has. Child. Parent) ⊔ Grandmother Woman ⊔ has. Child. Parent ⊔ Grandmother Note: means “equivalent” / “becomes” 17

The (beginning of the) proof (1)Grandmother(a) ⊓ Person(a) # An individual a for whom we are disproving the # theorem. (2) Apply ⊓-rule to (1): Grandmother(a) (3) Apply ⊓-rule to (1): Person(a) closed path (4) Grandmother ⊔ (Woman ⊓ has. Child. Parent) (5) Apply ⊔-rule to (4) : Grandmother(a) (6) Apply ⊔-rule to (4) : Woman ⊓ has. Child. Parent (7) Apply ⊓-rule to (6): Woman(a) (8) Apply ⊓-rule to (6): has. Child. Parent (9) Woman ⊔ (Person ⊓ Female) closed path (10) Apply ⊔-rule to (9): Woman(a) (11) Apply ⊔-rule to (9): Person ⊓ Female closed path (12) Apply ⊓-rule to (11): Person(a) (12) Apply ⊓-rule to (11): Female(a) (13) Person ⊔ Female ⊔ Woman all three paths (14) Apply ⊔-rule to (13): Person(a) are closed (14) Apply ⊔-rule to (13): Female(a) (14) Apply ⊔-rule to (13): Woman(a) 18

More reasoning tasks Note: the tableau above is not fully expanded. There are more formulas that can be transformed by means of ⊓-rule, ⊔-rule, -rule and -rule. To prove the original goal, we must show that all paths of the fully expanded tableau are closed. Although fully mechanical, this process is very tedious for a human – automated theorem provers like Pellet and Fact++ (both employed in Protégé) do a much better job. The classification task can be reduced to inconsistency checking as well. To prove that individual x is a member of class A, we can prove that A(x) is inconsistent instead. To find all members of a class (task called instance generation/retrieval), we must show A(x) for all x. To prove that a class A is inconsistent (i. e. has no members), we can add A(x) to the KB and show that the resulting set is inconsistent (i. e. assume that there is a member x A and proof a contradiction). To prove A ⊔ B (class disjointness), we can prove that adding A ⊓ B to the KB makes it inconsistent. 19

Inconsistency example Consider the following KB: Bear Animal ⊓ Omnivore eat. Animal Panda Bear ⊓ Vegetarian eat. Animal It is easy to see that this KB is inconsistent. Assume that there exists an individual x which is a member of the class Panda. Then: Panda(x) Bear(x) AND Vegetarian(x) x does not eat animals Bear(x) Animal(x) AND Omnivore(x) x eats animals Contradiction, therefore class Panda must be empty. Note: reasoning over defined classes ONLY! 20

DLs Reasoners: Pellet performs all three reasoning tasks that were discussed: i. Subsumption: prove that any instance of class A is an instance of B. This is the most basic reasoning task. It allows us to think of a single class hierarchy as we design the ontology and leave the job of inferring the multiple inheritance polyhierarchy to the reasoner. ii. Classification: prove that an individual x is a member of class A, i. e. A(x). iii. Inconsistency: prove that no individual is a member of some class A, in which case the ontology is considered inconsistent. Next, examples from Pizza ontology are used to illustrate these tasks.

Primitive and defined classes in Protege Recall from the Pizza tutorial that we distinguish between primitive classes and defined classes. The difference between them is that primitive classes state only necessary conditions for a class membership, while defined classes state both necessary and sufficient conditions for class membership. Consider class Cheesy. Pizza. It is defined as “any pizza with some cheese topping”. If you save Pizza ontology as. ttl file, you will see the following code for Cheesy. Pizza: : Cheesy. Pizza rdf: type owl: Class ; rdfs: sub. Class. Of : Pizza , [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: some. Values. From : Cheese. Topping ]. This definition does not allow us to derive that if an individual is a Pizza and it has some Cheese. Topping, then it must be a member of the class Cheesy. Pizza. To make this conclusion, we must say that not only all members of class Cheesy. Pizza are members have some Cheese. Topping, but also that all members of the anonymous restriction class are also members of class Cheesy. Pizza, i. e. to make the two classes equivalent. 22

Cheesy. Pizza as a defined classes Here is the “revised” definition of Cheesy. Pizza: : Cheesy. Pizza rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Pizza [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: some. Values. From : Cheese. Topping ] ) ; rdf: type owl: Class ]. That is, Cheesy. Pizza is now equivalent to a new class which is an intersection of class Pizza and the anonymous Restriction class along the property has. Topping. Reasoning is carried out only over defined classes. 23

Subsumption example: Pellet has derived the subclasses of Cheesy. Pizza 24

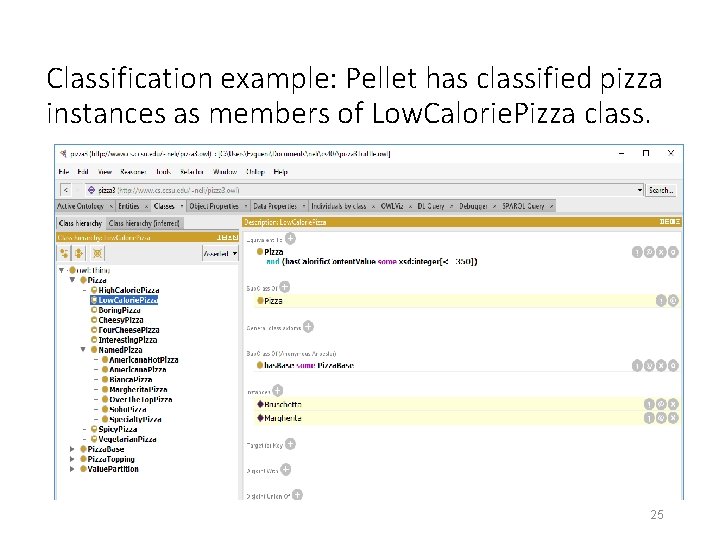
Classification example: Pellet has classified pizza instances as members of Low. Calorie. Pizza class. 25

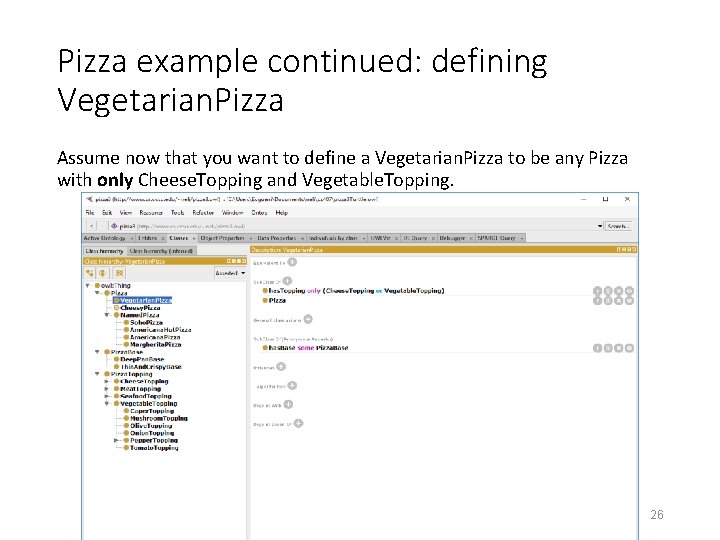
Pizza example continued: defining Vegetarian. Pizza Assume now that you want to define a Vegetarian. Pizza to be any Pizza with only Cheese. Topping and Vegetable. Topping. 26

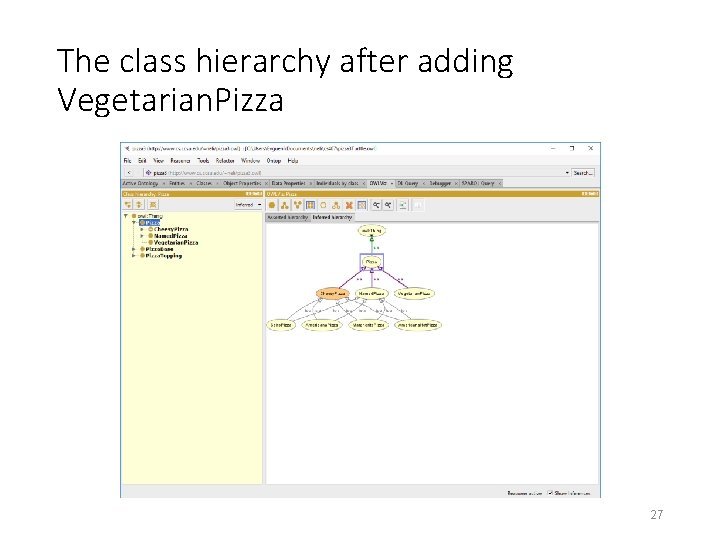
The class hierarchy after adding Vegetarian. Pizza 27

The reasoner classifies Vagetarian. Pizza as a Pizza, but to classify a named pizza as a Vegetarian. Pizza, we must convert the latter into a defined class, i. e. to state that any Pizza with ONLY Cheese. Topping and/or Vegetarian. Topping MUST be a Vegetarian Pizza (for ex. Margharita. Pizza must be a vegetarian Pizza – but NOTICE -- IT DOES NOT!). 28

Why Pellet does not classify Margherita. Pizza as a Vegetarian. Pizza? The role of the OWA As we have already discussed, DLs and thus OWL employ OWA. That is, we cannot assume something just because it is not stated explicitly. Although we have defined Margherita. Pizza to have cheese and tomato topping, under the OWA it is assumed that it may have other toppings as well which are not declared. Therefore, the answer to the question “Does Margherita. Pizza have other toppings than cheese and tomato? ” under the OWA is “Don’t know”. Under the CWA, the answer will be “NO”, but this assumption is not in place here. To enforce the “NO” answer (or kind-of CWA), we must impose the closure axiom on the has-topping property. The closure axiom on a property has. Topping for Margherita. Pizza is has. Topping (Mozzarella. Topping ⊔ Tomato. Topping) 29

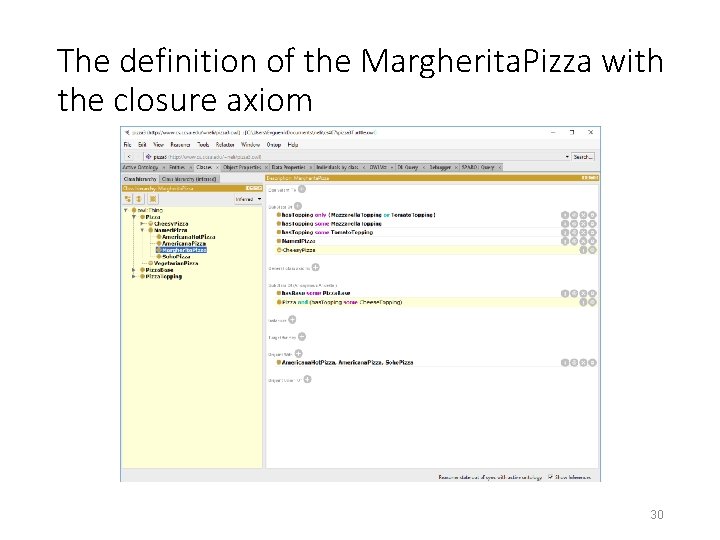
The definition of the Margherita. Pizza with the closure axiom 30

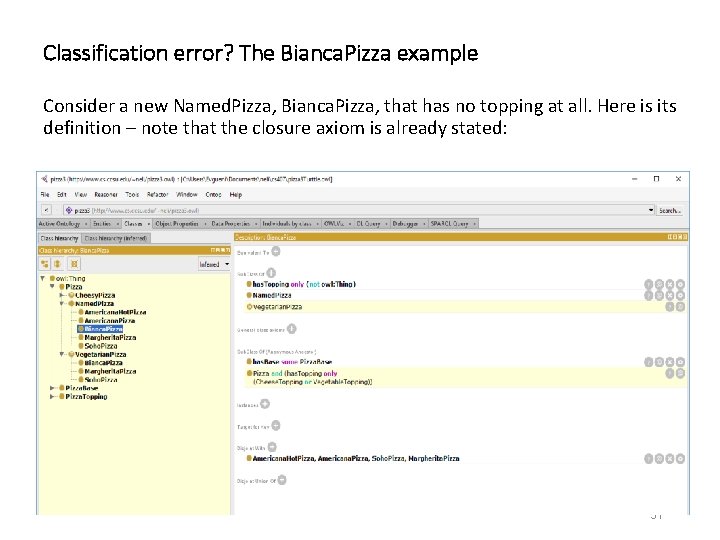
Classification error? The Bianca. Pizza example Consider a new Named. Pizza, Bianca. Pizza, that has no topping at all. Here is its definition – note that the closure axiom is already stated: 31

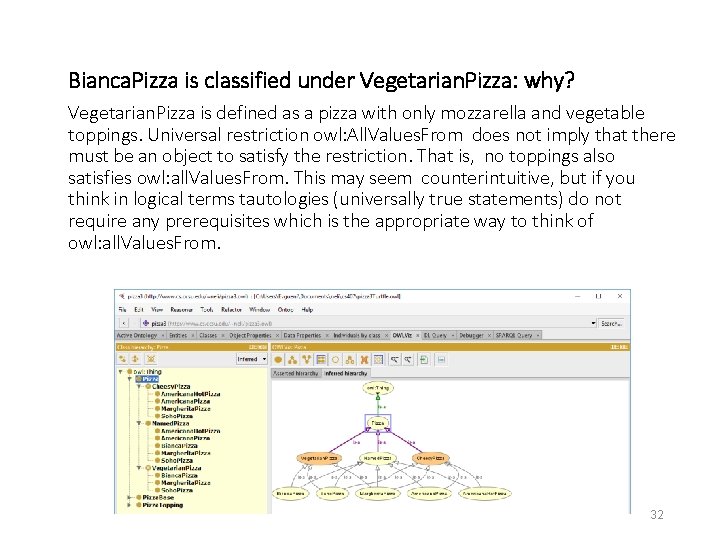
Bianca. Pizza is classified under Vegetarian. Pizza: why? Vegetarian. Pizza is defined as a pizza with only mozzarella and vegetable toppings. Universal restriction owl: All. Values. From does not imply that there must be an object to satisfy the restriction. That is, no toppings also satisfies owl: all. Values. From. This may seem counterintuitive, but if you think in logical terms tautologies (universally true statements) do not require any prerequisites which is the appropriate way to think of owl: all. Values. From. 32

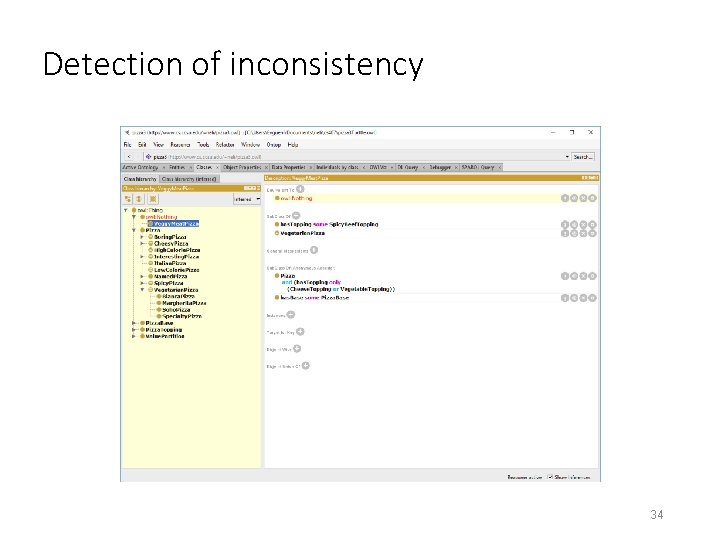
Inconsistency example: Untangling • Notice that each of the Named. Pizza subclasses were classified as subclasses of Cheesy. Pizza. The reasoner returns the inferred polyhierarchy (a hierarchy where classes may have multiple parents). This process of computing all implicit subsumptions in the ontology is called untangling. • While our original class hierarchy has an easy to build and maintain tree structure, the inferred polyhierarchy is a complex graph including all implicit relations between classes. • Untangling will also explicate inconsistencies in the ontology by identifying empty classes, i. e. classes that cannot have any members. Consider a new class Veggy. Meat. Pizza defined as a subclass of Vegetarian. Pizza with the following restriction on property has. Topping owl: some. Values. From Spicy. Beef. Topping Inferred hierarchy with detected inconsistency is shown next. 33

Detection of inconsistency 34

Notice that Veggy. Meat. Pizza is identified by the reasoner as an inconsistent class, i. e. a class that cannot have any members. It is very important in such cases to know what causes the inconsistency. Protégé explain inference feature (? option for owl: nothing on the Description panel) returns the following explanation for the detected inconsistency: 35

Cardinality restrictions in Protégé offers all three kinds of cardinality restrictions: • owl: qualified. Cardinality – specifies the exact number of relationships along a given property that an individual must participate in. • owl: min. Qualified. Cardinality – specifies the minimum number of relationships along a given property that an individual must participate in. • owl: max. Qualified. Cardinality – specifies the maximum number of relationships along a given property that an individual must participate in. Example: Boring. Pizza, a pizza with at most 1 toping : Boring. Pizza rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Pizza [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: max. Qualified. Cardinality "1"^^xsd: non. Negative. Integer ; owl: on. Class : Pizza. Topping ] ) ; rdf: type owl: Class ]. Bianca. Pizza will be classified as Boring. Pizza. 36

Cardinality restrictions in Protégé (contd. ) Example: Interesting. Pizza, a pizza with at least 3 toppings. : Interesting. Pizza rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Pizza [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: min. Qualified. Cardinality "3"^^xsd: non. Negative. Integer ; owl: on. Class : Pizza. Topping ] ) ; rdf: type owl: Class ]. Example: Four. Cheese. Pizza, a pizza with 4 cheeses toppings. : Four. Cheese. Pizza rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Pizza [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: qualified. Cardinality "4"^^xsd: non. Negative. Integer ; owl: on. Class : Cheese. Topping ] ) ; rdf: type owl: Class ]. 37

More pizza types: Specialty. Pizza Let us create Specialty. Pizza with only and exactly 4 cheese toppings, but possibly other topping as well. : Specialty. Pizza rdf: type owl: Class ; rdfs: sub. Class. Of : Named. Pizza , [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: all. Values. From : Cheese. Topping ], [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: qualified. Cardinality "4"^^xsd: non. Negative. Integer ; owl: on. Class : Cheese. Topping ]. Pellet will classify Specialty. Pizza as Vegetarian. Pizza and Four. Cheese. Pizza, which is, in turn, Interesting. Pizza and Cheesy. Pizza. 38

More pizza types: Over. The. Top. Pizza Consider also Over. The. Top. Pizza with 4 cheese toppings and at least 1 more any choice topping. : Over. The. Top. Pizza rdf: type owl: Class ; rdfs: sub. Class. Of : Named. Pizza , [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: min. Qualified. Cardinality "5"^^xsd: non. Negative. Integer ; owl: on. Class : Pizza. Topping ], [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: qualified. Cardinality "4"^^xsd: non. Negative. Integer ; owl: on. Class : Cheese. Topping ]. Pellet will classify Over. The. Top. Pizza as Four. Cheese. Pizza, which is, in turn, Interesting. Pizza and Cheesy. Pizza. 39

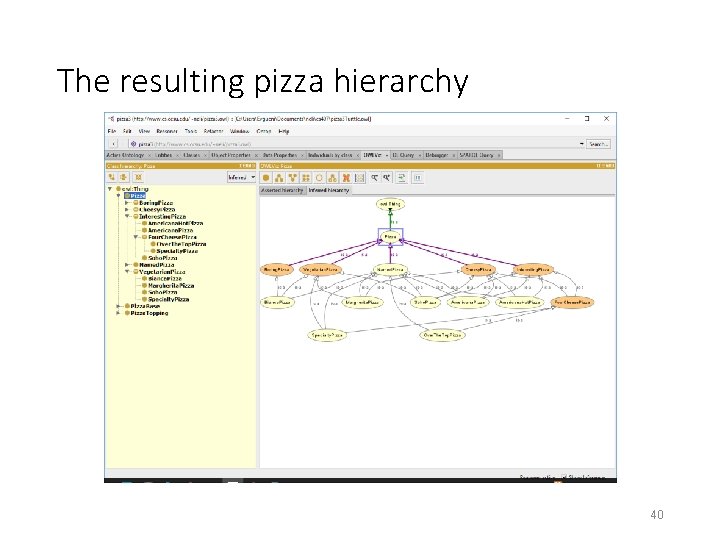
The resulting pizza hierarchy 40

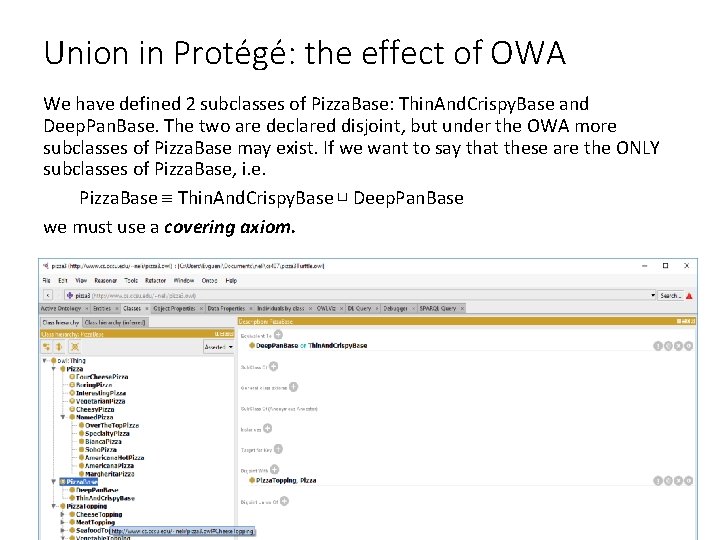
Union in Protégé: the effect of OWA We have defined 2 subclasses of Pizza. Base: Thin. And. Crispy. Base and Deep. Pan. Base. The two are declared disjoint, but under the OWA more subclasses of Pizza. Base may exist. If we want to say that these are the ONLY subclasses of Pizza. Base, i. e. Pizza. Base Thin. And. Crispy. Base ⊔ Deep. Pan. Base we must use a covering axiom. 41

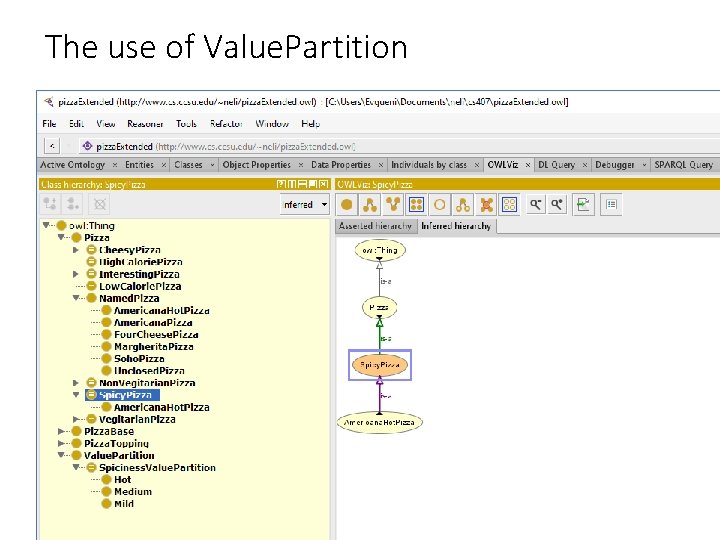
Value Partitions: a useful design pattern in ontology engineering to eliminate the need for a covering axiom We can create a “value partition” class to serve as a superclass of all union classes in the ontology. Example: Assume we have the following two value partitions Pizza. Base. Value. Partition Thin. And. Crispy. Base or Deep. Pan. Base (instead of covering Pizza. Base as done above) Spiciness. Value. Partition Hot or Medium or Mild To describe the spiciness of different types of toppings, let us have a new object property, has. Spiciness, and let us assign to all toppings some spiciness. Assume now that we want to create a new defined class Spicy. Pizza which has at least one topping with spiciness “Hot”, i. e. Spicy. Pizza and has. Topping some (Pizza. Topping and (has. Spyciness some Hot)) OR instead, we can create a new class Hot. Pizza. Topping and (has. Spyciness some Hot) 42

Spicy. Pizza: the definition : Spicy. Pizza rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Pizza [ rdf: type owl: Restriction ; owl: on. Property : has. Topping ; owl: some. Values. From [ owl: intersection. Of ( : Pizza. Topping [ rdf: type owl: Restriction ; owl: on. Property : has. Spiciness ; owl: some. Values. From : Hot ] ) ; rdf: type owl: Class ] ] ); rdf: type owl: Class ]. Notice that the outlined anonymous class defines the intersection of class Pizza. Topping and restriction class on individuals that has. Spiciness some Hot. The alternative way to define this would be to create a subclass of Pizza. Topping, Hot. Pizza. Topping, with the same restriction. Then, Spicy. Pizza would be defined as a 43 class of individuals that has. Topping some Hot. Pizza. Topping, as suggested above.

The use of Value. Partition 44

Introduction to Homework 4 project Assume that you are building an application for collecting demographic information about families (along the lines of US Census project) or an application to explicate hidden family or inter-family relations. First, you must build the domain model, something that we called ontological engineering. That is, ontological engineering is a set of tasks related to the development of ontologies for a particular domain. This includes: • Defining concepts/classes in the domain. • Arranging them in a subclass-superclass hierarchy, but no need to do this in a precise way, because it is the reasoner’s job to compute the final polyhierarchy. • Defining properties/relations and constraints on their values. • Defining individuals (if any) and filling in property values. Assume that the backbone of your ontology has already been done. You need to extend the current prototype according to a given specification. You have 2 example ontologies to work with (next two slides). Choose one for your project.

Example domain 1: [cs. ccsu. edu/~neli/Family. Project. owl] Interested to learn more about this project (may also help with the homework), see (voted session’s best paper ) https: //www. iiis. org/CDs 2020/CD 2020 Spring/papers/ZA 969 NZ. pdf

Example domain 2: [cs. ccsu. edu/~neli/Family. Project. Tiny 2. ttl] 47

48

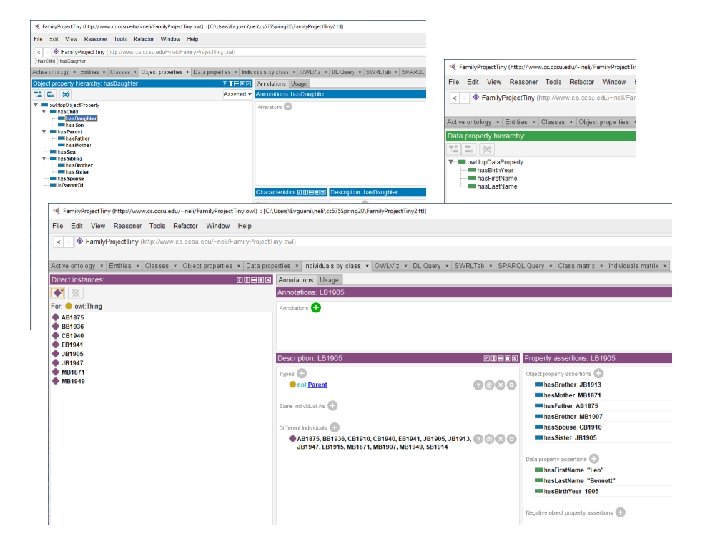
The A-box: Bennett family We want to reason about families (here the Bennett family) – who are the members of the extended family, family units, families with/without children, parents of 1/2/3… children, parents of girls/boys only, etc… all demographic information about families that you can think of. Individuals are defined in terms of: • Parents (has. Mother, has. Father) • Siblings (has. Brother, has. Sister) • Spouse (has. Spouse) • First name, Last name, Birthyear All individuals are of type owl: Named. Individual. Also all individuals are made different. If they would have not been made different, it would be assumed that some individuals have different name. That is, if you ask which families have at least 2 children, the answer would be incorrect because (of the Non-unique name assumption) families with 2, 3, etc. children would not be returned assuming that this might be just 1 child with 2, 3, etc. names. Note: Always make individuals DIFFERENT, and if the same individual has different names, use same. As to state that. 49

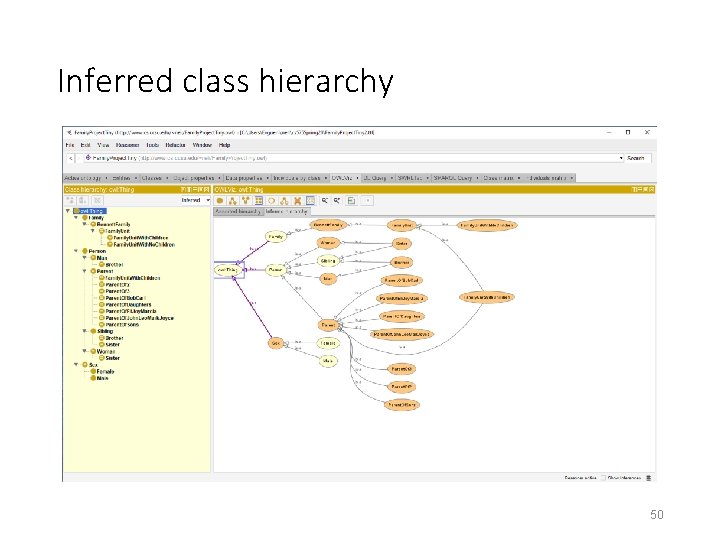
Inferred class hierarchy 50

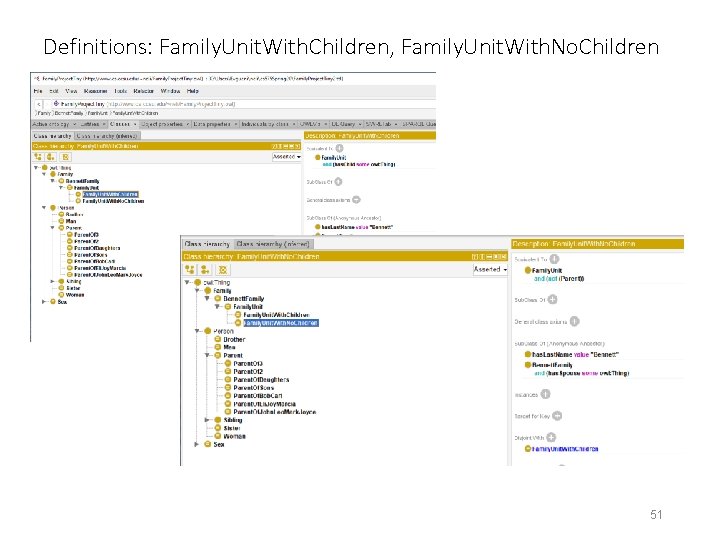
Definitions: Family. Unit. With. Children, Family. Unit. With. No. Children 51

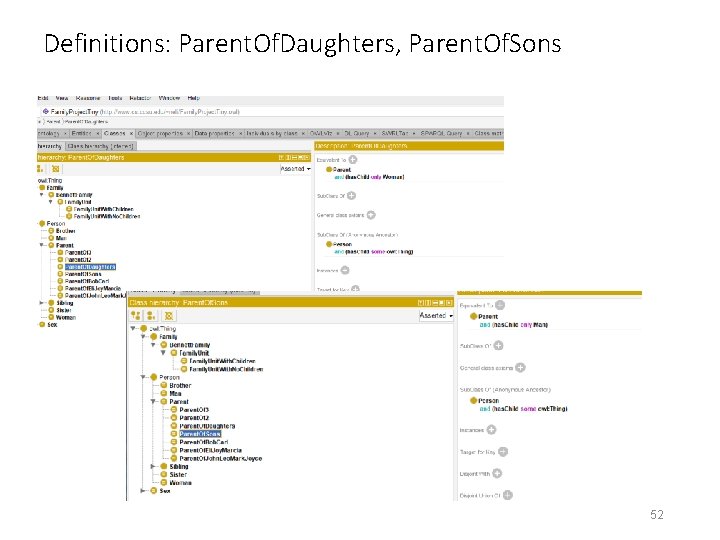
Definitions: Parent. Of. Daughters, Parent. Of. Sons 52

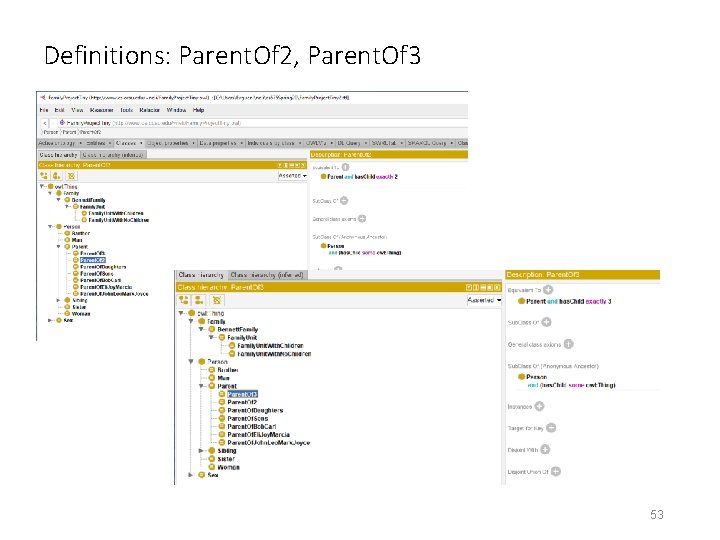
Definitions: Parent. Of 2, Parent. Of 3 53

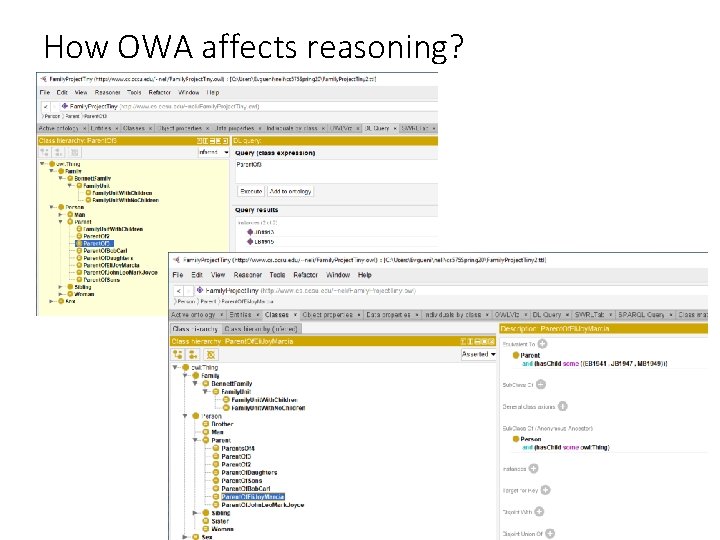
How OWA affects reasoning? 54

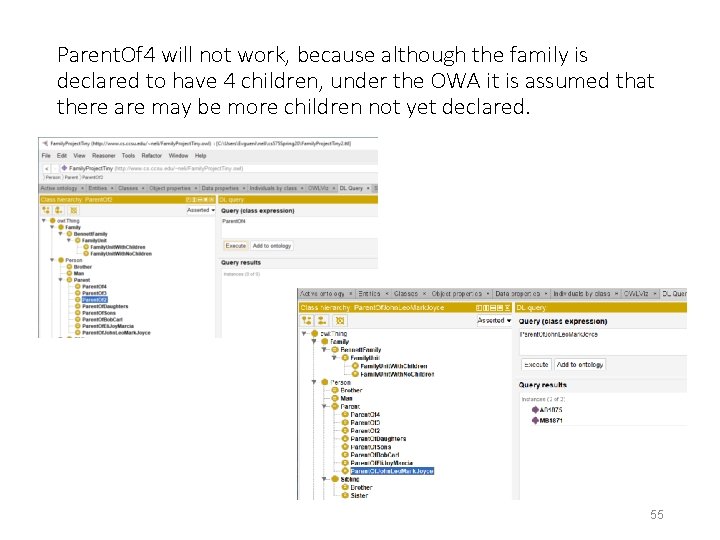
Parent. Of 4 will not work, because although the family is declared to have 4 children, under the OWA it is assumed that there are may be more children not yet declared. 55

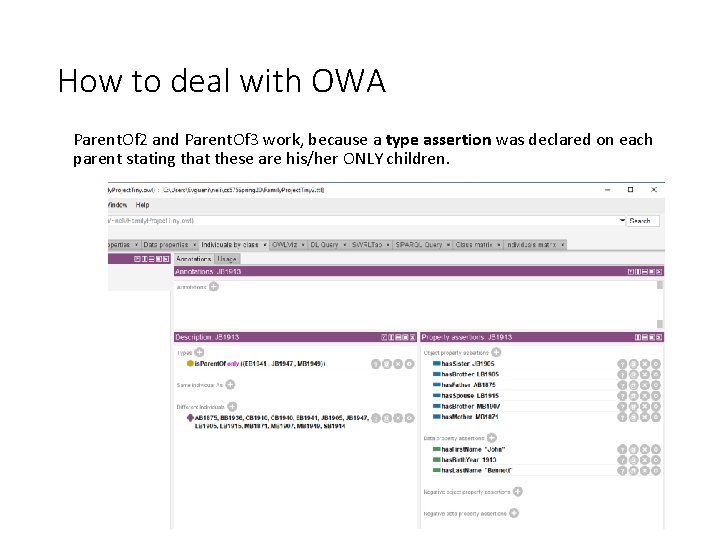
How to deal with OWA Parent. Of 2 and Parent. Of 3 work, because a type assertion was declared on each parent stating that these are his/her ONLY children. 56

The role of type assertions and more ways to deal with OWA Type assertions allow us to “close” the world. In example above, we say “JB 1913 has only 3 children are these are the once enumerated into the closed class {EB 1941, JB 1947, MB 1949}. That is, we enforce the CWA on the A-box. Note that such closure type assertions slow down the reasoner considerably. There are other ways to impose CWA on a domain. In Pizza example, value partitions and covering axioms do the same. Recall {Hot, Medium, Mild} were the only values for the Spaciness. Value. Partition, and the covering axiom states that Spaciness. Value. Partition Hot or Medium or Mild Notice that owl: all. Values. From also imposes a closure on the restriction and says that the subject of this property can ONLY be of the specified type. Example: Parent. Of. Daughters Parent and has. Child only Woman 57

Reasoning about classes vs reasoning about individuals • Similar in that both result is new triples being added to the data set. • Very different from a modelling perspective: • Reasoning about individuals draw conclusions about individuals (new triples added to the A-box). • Reasoning about classes draw general conclusions about classes (new triples added to the T-box). No individuals are involved in this case. Example: Family. Unit. With. Children is derived to be a subclass of Parent class. New derived triples are of the following types: o A rdfs: subclass. Of B o P rdfs: sub. Property. Of Q o A rdfs: domain B o A rdfs: range B All these new relations are reflected in the inferred structure of the dataset. 58