Selfsimilar analysis of various nonlinear partial differential equations

Self-similar analysis of various non-linear partial differential equations Imre Ferenc Barna Wigner Research Center of the Hungarian Academy of Sciences, Budapest 2 ELI-ALPS Nonprofit Kft Szeged 1

Outline • Introduction various PDEs, basic solutions self-similar, travelling wave , an example heat conduction • Systems I already investigated a list of various Navier-Stokes equations, heat conduction mechanisms, other physical systems • The Oberbeck-Bousinesq equ chaos versus solutions • Non-linear Maxwell equations plus ELI related idea • Summary & Outlook

The very basic of the idea Initially: a (nonlinear) partial differential equation (system) for u(x, t) is given Ansatz : combination from space and time variable x, t to a new variable η(x, t) so u(η) Result: a (nonlinear) ordinary differential equation (system) u’ (η) + with some tricks analytic solutions can be found which depend on some free physical parameter(s), general properties are interesting e. g. shock, compact support makes physics

The basic linear partial differential equations 1 no-time dependence we do not consider in the following 2 there is mathematical maximum principle for the solutions in time, dispersion, but infinite propagation speed for the solution, heat conduction or diffusion eq. 3 no-maximum principle for the solution, finite propagation speed, wave eq. There are well-behaving basic solutions for 2 -3 Idea: is to use these solutions for any kind of non-linear PDEs, to investigate how the wave or diffusive character are conserved, (ther is no theory for nonlin PDEs)

Physically important solutions of PDEs - Travelling waves: arbitrary wave fronts u(x, t) ~ g(x-ct), g(x+ct) - Self-similar in 1 D Sedov, Zeldovich, Barenblatt in Fourier heat-conduction

Physically important solutions of PDEs II - generalised self-similar: - one case: blow-up solution: goes to infinity in finite time other forms are available too - generalized travelling waves, exponential method

Physically important solutions of PDEs III - additional: additive separable multiplicative separable generalised separable eg. these are all Ansätze, there are methods too, eg. Lie algebra, Bäcklund transformation, Painleve analysis, and so

First example: ordinary diffusion/heat conduction equation U(x, t) temperature distribution Fourier law + conservation law • parabolic PDA, no time-reversal sym. • strong maximum principle ~ solution is smeared out in time • • the fundamental solution: general solution is: • • • kernel is non compact = inf. prop. Speed paradox of heat cond. Problem from a long time But have self-similar solution

Very first example: how the method works General remarks: 1) No contradiction among the exponents = exists a dissipative solution it is not always a case 2) No extra free parameters, eg. equation of state, all the parameters are fixed, no different , solutions/physics for different materials

Systems I investigated till now non-linear heat conduction in solids in 1 D various Navier-Stokes equations in 2 d or 3 d generalised Fourier heat conduction laws compressible, noncompressible, Newtonian and non-Newtonian shock wave solutions, compact support 2 published papers 1 in progress 3 published papers Coupling the two effects, most interesting field 2 published papers, 1 in progress I will explain in details non-linear Maxwell equations field dependent material equations, analogy came from Fourier heat cond. 1 published papers 1 work is in progress ELI related I will explain in details

Various hydrodynamical equations Starting point: Ideal compressible flow, continuity equation + Euler equation based on conservation laws (no heat exchange) (in 1 dimension) how to go further? Incompressibility or + Equation of state Bernulli Eq. eg. or + extra terms, viscosity Navier-Stokes

Various dissipative fluid equations Non-compressible and Newtonian (I) Compressible and Newtonian (II) 0 Non-compressible and Non. Newtonian (III) (an example) Compressible and Non-Newtonian tooo complicated, we will see… Euler description, v velocity field, p pressure, a external field viscosity, density, kompressibility, E stress tensor, n behav. ind.

Various dissipative fluid equations Non-compressible and Newtonian (I) I. F. Barna Compressible and Newtonian (II) I. F. Barna, L. Mátyás Non-compressible and Non. Newtonian (III) Compressible and Non-Newtonian tooo complicated, we will see… Commun in Theor. Phys. 56, (2011) 745 I. F. Barna, G. Bognár, K. Hriczó Mathematical Modelling and Analysis 21, (2016) 83 Fluid Dyn. Res. 46, (2014) 055508 Critique: not much modelling, just solving the basic equations

Other analytic solutions all are for non-compressible N-S Without completeness, usually from Lie algebra studies Presented 19 various solutions one of them is: Ansatz: Solutions are Kummer functions as well “Only” Radial solution for 2 or 3 D Ansatz: Sedov, stationary N-S, only the angular part

Other Analytic solutions • the Russians and the NASA have probably even more… Sometimes I find scientific reports – for flows - which were confidental 40 years ago • “The results are sometimes difficult to find because the studies were conducted in the last century and often published in reports of limited circulation”

My 3 dimensional Ansatz A more general function does not work for N-S Geometrical meaning: all v components with coordinate constrain x+y+z=0 lie in a plane = equivalent The final applied forms

The second example - the Oberbeck-Boussinesq pde system - two-dimensional Navier-Stokes equation coupled to heat conduction via Boussinesq approx. (the simplest way) - exhaustively investigated system, the first meteorological model for the atmosphere NS. for the x horiz. cor. NS. for the z vert. cord. heat conduction eq. continuity eq.

Oberbeck-Boussinesq PDE system - investigated via stream function with Fourier expansion, can lead to chaotic ODE systems highly truncated, considering only 1 term strange attractor

Our applied Ansatz, self. -sym. exponents and the ODE system, we investigate the original hydrodynamical system (use the evarage temperature) positive exponents, mean dissipative solutions note: ½ is a simple diffusion exponent, pressure and temperature behave differently the remaining ODE system can be solved analytically

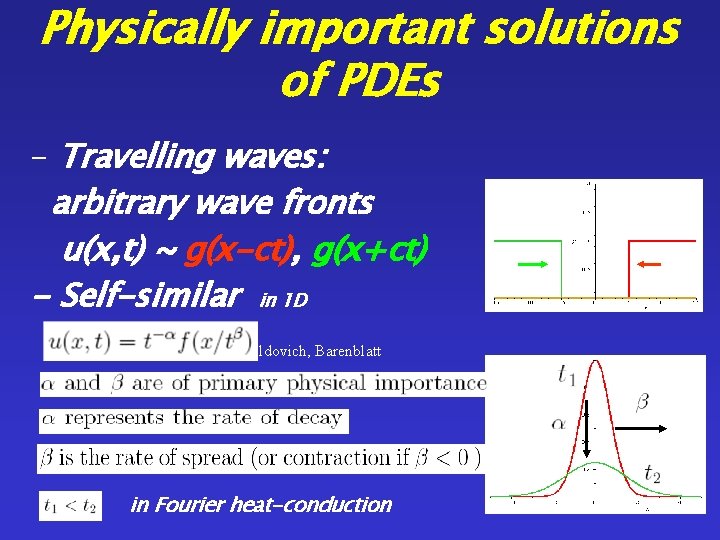
The temperature field Eq. 3 separates from Eq. 1 -2 can be expressed with the help of the Error functions For fixed t and x T(x) has the same shape so any inhomogenity can start the Rayleigh- Bénard convection this is the main result Chaos solitons and fractals 78 (2015) 249

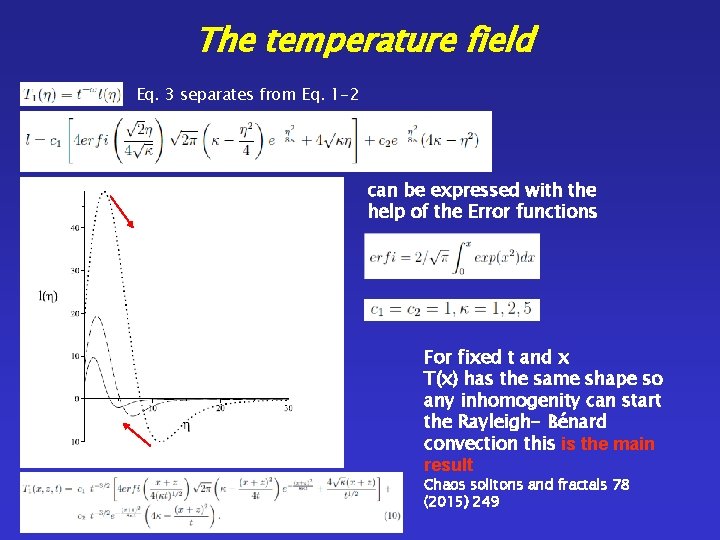
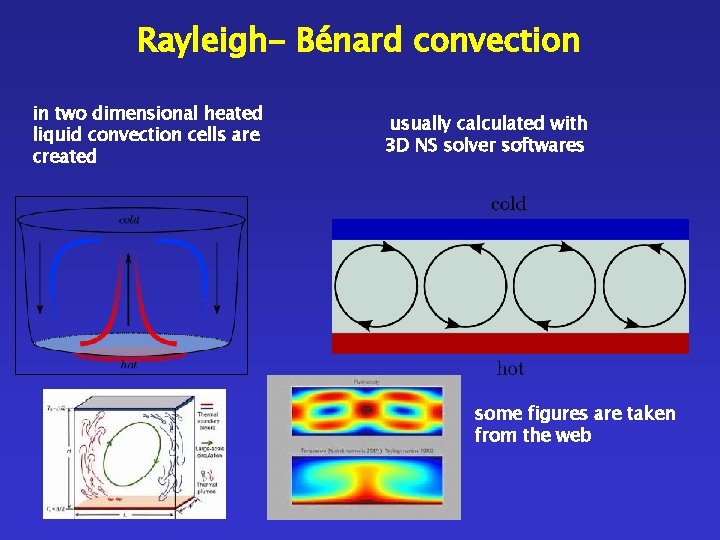
Rayleigh- Bénard convection in two dimensional heated liquid convection cells are created usually calculated with 3 D NS solver softwares some figures are taken from the web

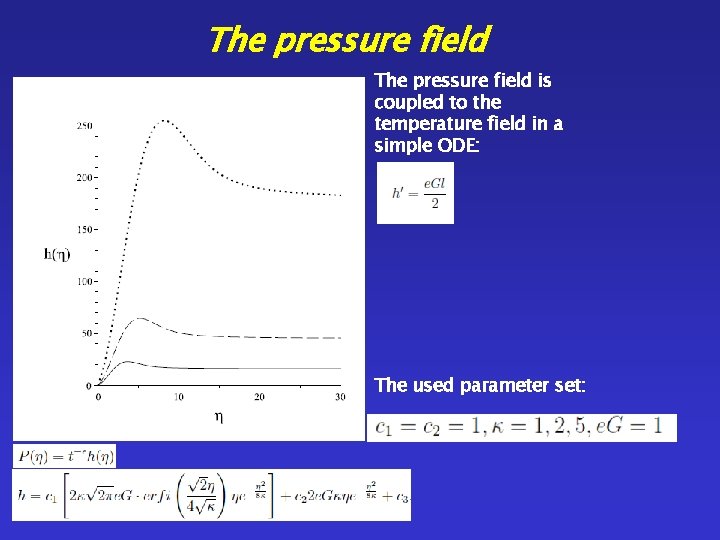
The pressure field is coupled to the temperature field in a simple ODE: The used parameter set:

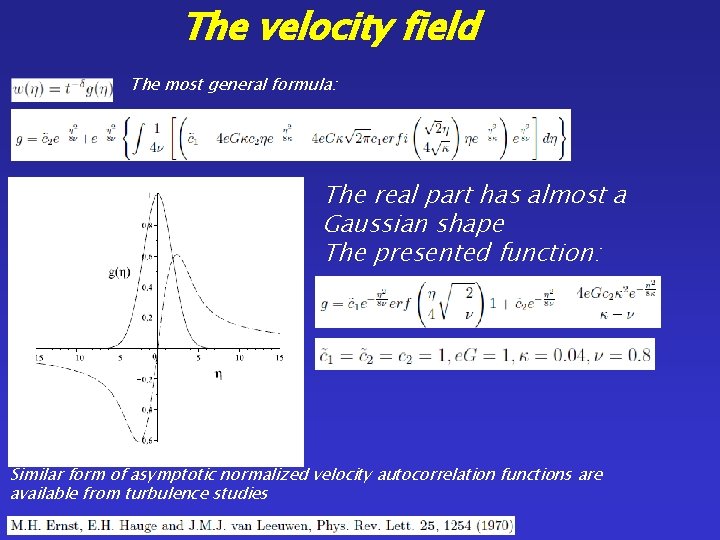
The velocity field The most general formula: The real part has almost a Gaussian shape The presented function: Similar form of asymptotic normalized velocity autocorrelation functions are available from turbulence studies

Additional remarks From the velocity field the, enstropy (the vorticity) can be calculated , the Fourier transform can be calculated as well to compare to turbulence studies Self-similar has some connection to: scaling, universality and renormalisation , critical phenomena , (but no clear cut understanding for me…) A generalization of the system is under investigation power-law temperature dependent viscosity and/or heat conduction can be considered as physical examples for ocean or other liquid media

The third example: non-linear Maxwell equations The field equations: The constitutive Eqs + differential Ohm’s Law Our consideration, power law: But: the exponent is a free physical parameter:

Geometry & Applied Ansatz

The final ordinary differential equations ’ means derivation with respect to eta Universality relations among the parameters: The first equ. is a total difference so can be integrated : Remaining a simple ODE with one parameter q (material exponent):

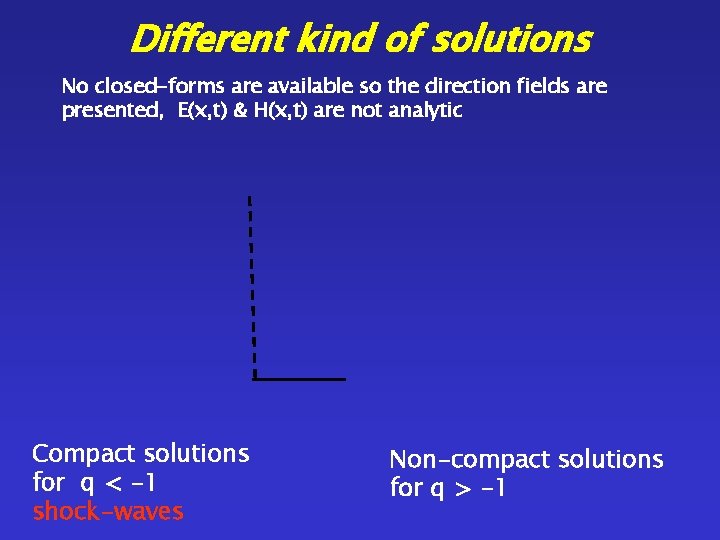
Different kind of solutions No closed-forms are available so the direction fields are presented, E(x, t) & H(x, t) are not analytic Compact solutions for q < -1 shock-waves Non-compact solutions for q > -1

Physically relevant solutions We consider the Poynting vector which gives us the energy flux (in W/m^2) in the field Unfortunatelly, there are two contraversial definition of the Poynting vector in media, unsolved problem R. N. Pfeifer et al. Rev. Mod. Phys. 79 (2007) 1197. published: I. F. Barna Laser Phys. 24 (2014) 086002 & ar. Xiv : http: //arxiv. org/abs/1303. 7084

Non-linear electrodynamics - In 1934 Born-Infeld proposed non-linear ED to remove point-like-particles induced singularities in field theories - above the Schwinger limit 1029 W/cm 2 intensities the dielctric response of vacuum itself becomes non-linear (very long range ELI interest ) - Lagrange density for linear versus non-lin ED after variation we get the equation of motion for the fields we, Polner M. , Mati P. Barna IF. investigate it

Summary we presented physically important, self-similar solutions for various PDEs as a first example we investigated Gaussian heatconduction as second example a spec. hydrodinamical system was analysed as a third example we investigated the 1 dim. Maxwell equations (instead fo the wave equation) closing with non-linear (power law) constitutive equations

Questions, Remarks, Comments? …