Self Organizing Maps A major principle of organization

Self Organizing Maps A major principle of organization is the topographic map, i. e. groups of adjacent neurons process information from neighboring parts of the sensory systems. Topographic maps can be distorted in the sense that the amount of neurons involved is more related to the importance of the task performed, than to the size of the region of the body surface that provides the input signals. 3/9/2021 Rudolf Mak TU/e Computer Science 1

Brain Maps A part of the brain that contains many topographic maps is the cerebral cortex. Some of these are: • Visual cortex – Various maps, such as retinotopic map • Somatosensory cortex – Somatotopic map • Auditory cortex – Tonotopic map 3/9/2021 Rudolf Mak TU/e Computer Science 2

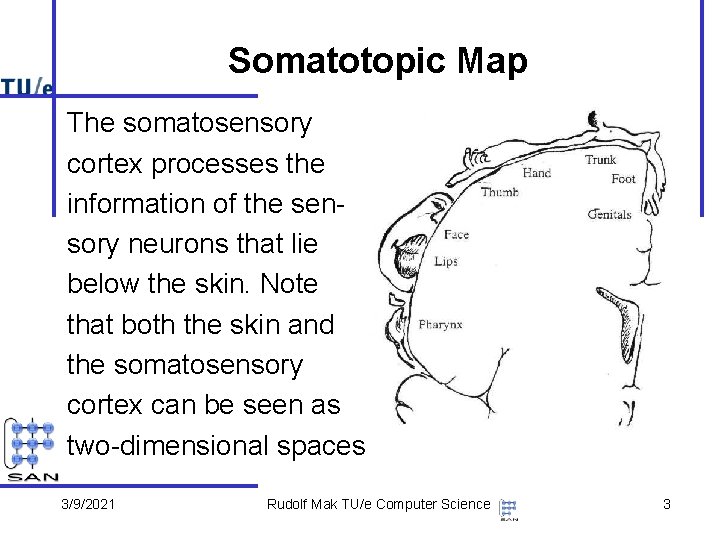
Somatotopic Map The somatosensory cortex processes the information of the sensory neurons that lie below the skin. Note that both the skin and the somatosensory cortex can be seen as two-dimensional spaces 3/9/2021 Rudolf Mak TU/e Computer Science 3

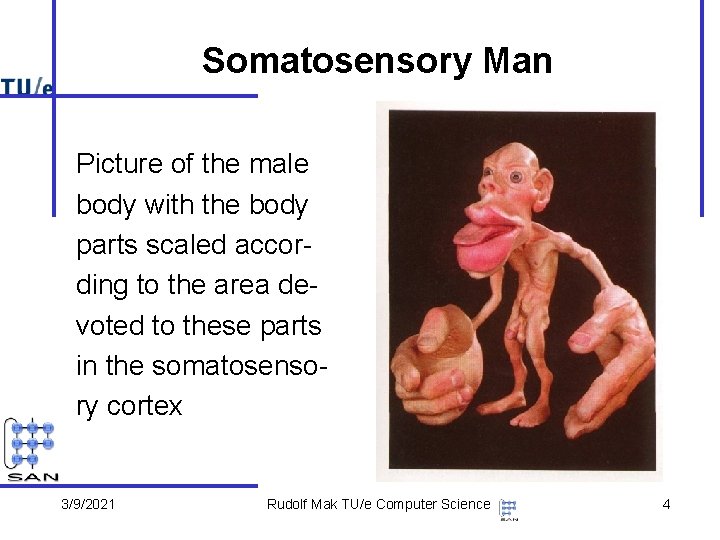
Somatosensory Man Picture of the male body with the body parts scaled according to the area devoted to these parts in the somatosensory cortex 3/9/2021 Rudolf Mak TU/e Computer Science 4

Unsupervised Selforganizing Learning • The neurons are arranged in some grid of fixed topology • The winning neuron is the neuron with its weight vector nearest to the supplied input vector • In principle all neurons are allowed to change their weight • The amount of change of a neuron, however, depends on the distance (in the grid) of that neuron to the winning neuron. Larger distance implies smaller change. 3/9/2021 Rudolf Mak TU/e Computer Science 5

Grid Topologies The following topologies are frequently used • One-dimensional grids – Line – Ring • Two-dimensional grids – Square grid – Torus – Hexagonal grid If additional knowledge of the input space is available more sophisticated topologies can be used. 3/9/2021 Rudolf Mak TU/e Computer Science 6

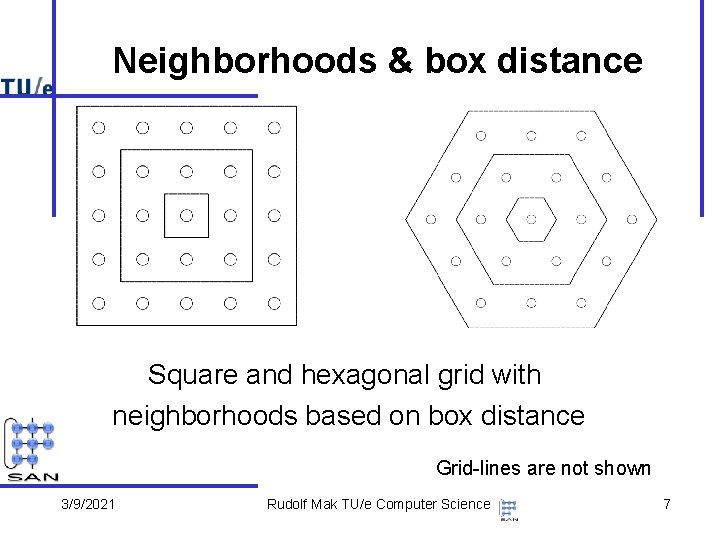
Neighborhoods & box distance Square and hexagonal grid with neighborhoods based on box distance Grid-lines are not shown 3/9/2021 Rudolf Mak TU/e Computer Science 7

Manhattan or Link Distance to the central cell measured in number of links 3/9/2021 4 3 2 3 4 3 2 1 2 3 2 1 0 1 2 3 2 1 2 3 4 3 2 3 4 Rudolf Mak TU/e Computer Science 8

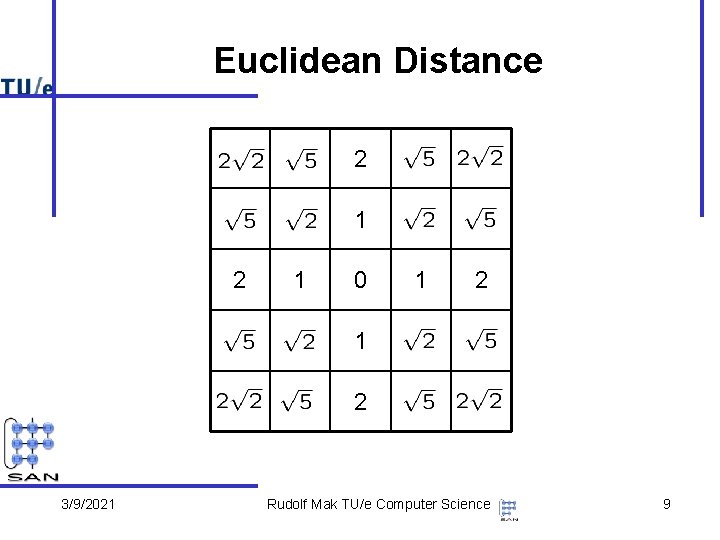
Euclidean Distance 2 1 0 1 2 3/9/2021 Rudolf Mak TU/e Computer Science 9

Topologically Correct Maps The aim of unsupervised self-organizing learning is to construct a topologically correct map of the input space. For any two neurons i and j in the grid, let d(i, j) be their fixed distance in the grid. A mapping is called topological correct when 3/9/2021 Rudolf Mak TU/e Computer Science 10

Neighborhood Functions The allowed weight change of neuron j when i is the winning neuron is given by the neighborhood function h(i, j). Common choices are: 1. 2. 3. 3/9/2021 (Winner takes it all) Rudolf Mak TU/e Computer Science 11

Unsupervised Self-organizing Learning (incremental version) 3/9/2021 Rudolf Mak TU/e Computer Science 12

Unsupervised Self-organizing Learning (batch version) 3/9/2021 Rudolf Mak TU/e Computer Science 13

Error Function For a network with weight matrix W and training set we define the error function E(W) by Let 3/9/2021 , then Rudolf Mak TU/e Computer Science 14

Gradients of the Error functions Because It follows that the gradient of the error is given by 3/9/2021 Rudolf Mak TU/e Computer Science 15

Tuning the Learning Process The learning process usually consists of two phases: 1. A phase in which the weight vectors reorder and become disentangled. In this phase neighborhoods (b) must be large. 2. A phase in which the weight vectors are finetuned to the part of the training set for which they are the respective winners. In this phase the neighborhoods (b) must be small to avoid interference from other neurons. 3/9/2021 Rudolf Mak TU/e Computer Science 16

Phonotopic Map • Input vectors are 15 dimensional speech samples from the Finnish language • Each vector component represents the average output power over 10 ms interval in a certain range of the spectrum (200 Hz – 6400 Hz) • Neurons are organized in a 8 x 12 hexagonal grid • After formation of the map, the individual neurons were calibrated to represent phonemes • The resulting map is called the phonetic typewriter 3/9/2021 Rudolf Mak TU/e Computer Science 17

Phonetic Typewriter The phonetic typewriter is constructed by Tuevo Kohonen, see e. g. his book “Self-Organizing Maps”, Springer, 1995. 3/9/2021 Rudolf Mak TU/e Computer Science 18

Travelling Salesman Problem TSP is one of the notorious difficult (NP-Complete) combinatorial optimization problems. The so-called elastic net method can be used to (approximately) solve the Euclidean version of this problem (Durbin and Willshaw). To that end one uses a SOM in which the neurons are arranged in a one-dimensional cycle. http: //www. patol. com/java/TSP/index. html 3/9/2021 Rudolf Mak TU/e Computer Science 19

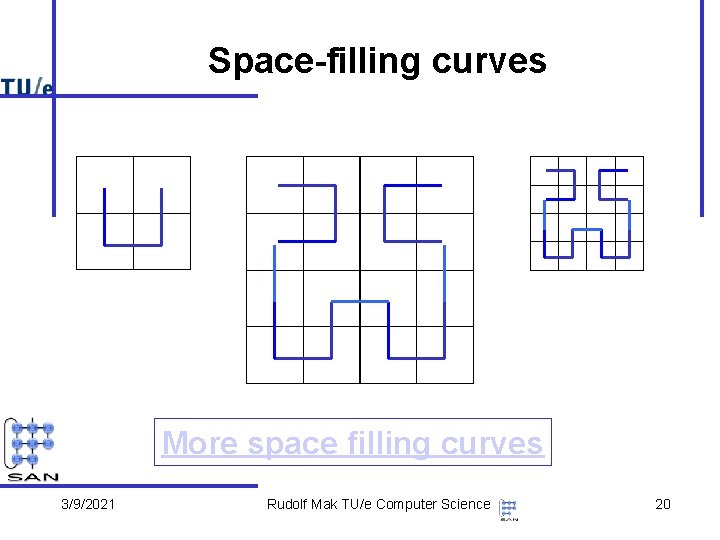
Space-filling curves More space filling curves 3/9/2021 Rudolf Mak TU/e Computer Science 20