Selected Algebraic System Examples from Lectures Matlab Examples
Selected Algebraic System Examples from Lectures
![Matlab Examples Matrix addition >> A=[1 3 2; 2 4 5]; >> B=[3 -4](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-2.jpg "Matlab Examples Matrix addition >> A=[1 3 2; 2 4 5]; >> B=[3 -4")
Matlab Examples Matrix addition >> A=[1 3 2; 2 4 5]; >> B=[3 -4 6; 1 -2 5]; >> D=A+B D = 4 -1 8 3 2 10 l Matrix multiplication >> C=[2 3; -1 2; 4 -3]; >> E=A*C E=7 3 20 -1 l
Gaussian Elimination Example l Form augmented matrix l Eliminate x 1 from second and third equations
Gaussian Elimination Example l Eliminate x 2 from third equation l Solve triangular system
Matlab Example Ax = b x = A-1 b (discuss next lecture) >> A=[3 -2 2; -5 4 -3; -4 3 -2]; >> rank(A) ans = 3 >> b=[-1; 3; 1]; >> x=inv(A)*b x = 3. 0000 -2. 0000
![Determinant Examples l By hand Using Matlab >> A=[1 2; 3 4]; >> det(A)](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-6.jpg "Determinant Examples l By hand Using Matlab >> A=[1 2; 3 4]; >> det(A)")
Determinant Examples l By hand Using Matlab >> A=[1 2; 3 4]; >> det(A) ans = -2 >> A=[1 2 3; 4 5 6; 7 8 9]; >> det(A) ans = 0 l
Gauss-Jordan Elimination l Eliminate x 2 entry from third row l Make the diagonal elements unity
Gauss-Jordan Elimination cont. l Eliminate first two entries in third column l Obtain identity matrix l Matrix inverse
Gauss-Jordan Elimination cont. l Verify result
![Matlab Examples >> A=[-1 1 2; 3 -1 1; -1 3 4]; >> inv(A)](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-10.jpg "Matlab Examples >> A=[-1 1 2; 3 -1 1; -1 3 4]; >> inv(A)")
Matlab Examples >> A=[-1 1 2; 3 -1 1; -1 3 4]; >> inv(A) ans = -0. 7000 0. 2000 0. 3000 -1. 3000 -0. 2000 0. 7000 0. 8000 0. 2000 -0. 2000 >> A=[1 2; 3 5]; >> b=[1; 2]; >> x=inv(A)*b x= -1. 0000
Ill-Conditioned Matrix Example l Example » e represents measurement error in b 2 » Two rows (columns) are nearly linearly dependent l Analytical solution l 10% error (e = 0. 1)
![Matlab Example >> A=[1 2; 3 5]; >> cond(A) ans = 38. 9743 (well](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-12.jpg "Matlab Example >> A=[1 2; 3 5]; >> cond(A) ans = 38. 9743 (well")
Matlab Example >> A=[1 2; 3 5]; >> cond(A) ans = 38. 9743 (well conditioned) >> A=[0. 9999 -1. 0001; 1 -1]; >> cond(A) ans = 2. 0000 e+004 (poorly conditioned) >> b=[1; 1. 1] >> x=inv(A)*b x= 500. 5500 499. 4500
![Matlab: Vector and Matrix Norms >> x=[2 -3 0 1 -4]'; >> norm(x, 2)](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-13.jpg "Matlab: Vector and Matrix Norms >> x=[2 -3 0 1 -4]'; >> norm(x, 2)")
Matlab: Vector and Matrix Norms >> x=[2 -3 0 1 -4]'; >> norm(x, 2) ans = 5. 4772 >> norm(x, inf) ans = 4 >> A = [5 1 1; 1 4 2; 1 2 4]; >> norm(A, 1) ans = 7 >> norm(x, inf) ans = 7 >> norm(A, 'fro') ans = 8. 3066
Condition Number l l Definition: k(A) = ||A|| ||A-1|| A “large” condition number indicates an ill-conditioned matrix l Well conditioned matrix l Ill-conditioned matrix
Condition Number cont. l Effect of data errors » Small data errors can lead to large solution errors » Bound can be very conservative l Example
Matlab: Condition Number >> A = [5 1 1; 1 4 2; 1 2 4]; >> AI = inv(A) AI = 0. 2143 -0. 0357 0. 3393 -0. 1607 -0. 0357 -0. 1607 0. 3393 >> norm(A, 1)*norm(AI, 1) ans = 3. 7500 >> cond(A, 1) ans = 3. 7500 >> norm(A, inf)*norm(AI, inf) ans = 3. 7500 >> cond(A, inf) ans = 3. 7500
Overdetermined Systems cont. l Normal equations: (ATA)x = ATb l Solution: x = (ATA)-1 ATb » ATA must be nonsingular » (ATA)-1 AT is called the left inverse matrix l Example
Underdetermined Systems cont. l Example
![Matlab: Linear Algebraic Systems >> A=[-1 1 2; 3 -1 1; -1 3 4];](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-19.jpg "Matlab: Linear Algebraic Systems >> A=[-1 1 2; 3 -1 1; -1 3 4];")
Matlab: Linear Algebraic Systems >> A=[-1 1 2; 3 -1 1; -1 3 4]; >> b=[1 2 3]'; >> x=inv(A)*b x= 0. 6000 0. 4000 0. 6000 >> x = linsolve(A, b) x= 0. 6000 0. 4000 0. 6000 >> x=Ab x= 0. 6000 0. 4000 0. 6000
![Matlab: Linear Algebraic Systems cont. >> A = [1 2; 2 -1; -2 -1];](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-20.jpg "Matlab: Linear Algebraic Systems cont. >> A = [1 2; 2 -1; -2 -1];")
Matlab: Linear Algebraic Systems cont. >> A = [1 2; 2 -1; -2 -1]; >> b = [25 -25]'; >> x = linsolve(A, b) x= -1. 0000 17. 0000 >> A=[1 2 -2; 2 -1 -1]; >> b=[25 -25]'; >> x = linsolve(A, b) x= -5. 0000 15. 0000 not equal to 0 x= -7 13. 5 2. 5
![Plotting a Function » x = [0. 1: 10]; » y 1 = 7*x.](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-21.jpg "Plotting a Function » x = [0. 1: 10]; » y 1 = 7*x.")
Plotting a Function » x = [0. 1: 10]; » y 1 = 7*x. /(0. 6 + x); » y 2 = 5*x. / (0. 08+x); » plot(x, y 1, x, y 2) » xlabel('x') » ylabel('y') » legend('y 1', 'y 2') » figure » subplot(2, 1, 1) » plot(x, y 1) » ylabel('y 1') » subplot(2, 1, 2) » plot(x, y 2) » ylabel('y 2')
![Square Systems >>A=[-1 1 2; 3 -1 1; -1 3 4]; >> b=[2 6](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-22.jpg "Square Systems >>A=[-1 1 2; 3 -1 1; -1 3 4]; >> b=[2 6")
Square Systems >>A=[-1 1 2; 3 -1 1; -1 3 4]; >> b=[2 6 4]'; >> x=inv(A)*b; >> x=Ab; >> x=linsolve(A, b) x= 1. 0000 -1. 0000 2. 0000
![Non-Square Systems >> A = [1 2; 2 -1; -2 -1]; >> b =](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-23.jpg "Non-Square Systems >> A = [1 2; 2 -1; -2 -1]; >> b =")
Non-Square Systems >> A = [1 2; 2 -1; -2 -1]; >> b = [25 -25]'; >> x=Ab x= -1. 0000 17. 0000 >> x = linsolve(A, b) x= -1. 0000 17. 0000
Distinct Real Eigenvalue Example l Characteristic matrix l Characteristic equation l Eigenvalues: l 1 = -5, l 2 = 2
Distinct Real Eigenvector Example l Eigenvalues l Determine eigenvectors: Ax = lx l Eigenvector for l 1 = -5 l Eigenvector for l 1 = 2
Repeated Real Eigenvalue Example l Characteristic matrix l Characteristic equation l Eigenvalues: l 1 = 2, l 2 = 2
Repeated Real Eigenvector Example l Eigenvalues l Determine eigenvectors: Ax = lx l Eigenvectors for l = 2 l Eigenvectors are linearly dependent
![Matlab Example >> A=[2 5; 0 2]; >> e=eig(A) e= 2 2 >> [X,](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-28.jpg "Matlab Example >> A=[2 5; 0 2]; >> e=eig(A) e= 2 2 >> [X,")
Matlab Example >> A=[2 5; 0 2]; >> e=eig(A) e= 2 2 >> [X, e]=eig(A) X= 1. 0000 -1. 0000 0 0. 0000 e= 2 0 0 2
Complex Eigenvalue Example l Characteristic matrix l Characteristic equation l Eigenvalues: l 1 = -1+i, l 2 = -1 -i
Complex Eigenvector Example l Eigenvalues l Determine eigenvectors: Ax = lx l Eigenvector for l = -1+i l Eigenvector for l = -1 -i
![Matlab Example >> A=[-1 -1; 1 -1]; >> e=eig(A) e= -1. 0000 + 1.](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-31.jpg "Matlab Example >> A=[-1 -1; 1 -1]; >> e=eig(A) e= -1. 0000 + 1.")
Matlab Example >> A=[-1 -1; 1 -1]; >> e=eig(A) e= -1. 0000 + 1. 0000 i -1. 0000 - 1. 0000 i >> [X, e]=eig(A) X= 0. 7071 0 - 0. 7071 i 0 + 0. 7071 i e= -1. 0000 + 1. 0000 i 0 0 -1. 0000 - 1. 0000 i
Matrix Diagonalization Example
![Matlab Example >> A=[-1 2 3; 4 -5 6; 7 8 -9]; >> [X,](http://slidetodoc.com/presentation_image_h2/64766d357e2b3642f0d4ea83d4dbad50/image-33.jpg "Matlab Example >> A=[-1 2 3; 4 -5 6; 7 8 -9]; >> [X,")
Matlab Example >> A=[-1 2 3; 4 -5 6; 7 8 -9]; >> [X, e]=eig(A) X= -0. 5250 -0. 6019 -0. 1182 -0. 5918 0. 7045 -0. 4929 -0. 6116 0. 3760 0. 8620 e= 4. 7494 0 0 0 -5. 2152 0 0 0 -14. 5343 >> D=inv(X)*A*X D= 4. 7494 -0. 0000 -5. 2152 -0. 0000 -14. 5343
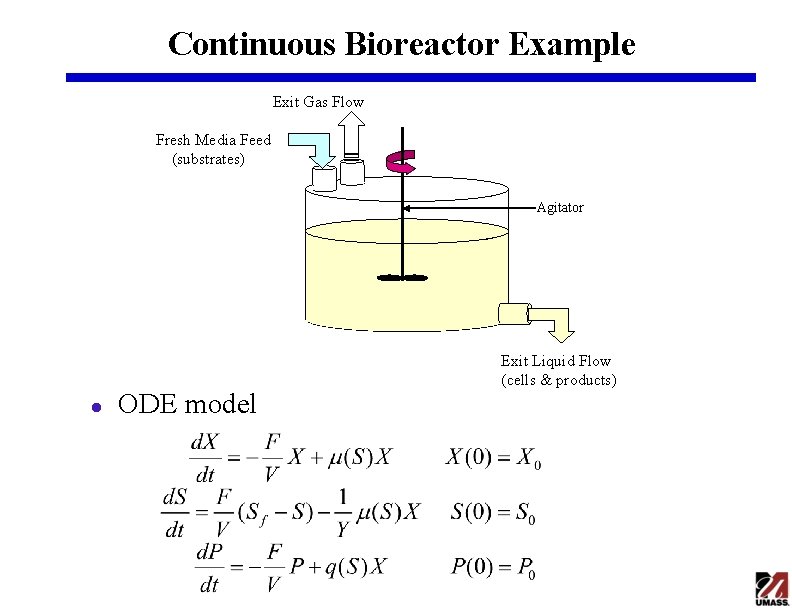
Continuous Bioreactor Example Exit Gas Flow Fresh Media Feed (substrates) Agitator l ODE model Exit Liquid Flow (cells & products)
Bioreactor: Fixed-Point Solution l Steady-state biomass equation l Iterative equation l Initialization:
Bioreactor: Newton-Raphson Solution l Iterative equation l Function l Derivative
Bioreactor: Secant Solution l Iterative equation l Function l Initialization:
Matlab Example #1 l l l Solution of a single nonlinear algebraic equation: Create Matlab m-file function: fun. m: Call fzero from the Matlab command line to find the solution: >> xo = 0; >> fzero('fun', xo) ans = 0. 5376 l Different initial guesses, xo, give different solutions: >> fzero('fun', 1) ans = 1. 2694 >> fzero('fun', 4) ans = 3. 4015
Matlab Example #2 l l l Solution of biomass equation Parameter values: D=0. 04 h-1, mm=0. 48 h-1, Km=1. 2 g/L, Ki=22 g/L Create Matlab M-file: substrate. m function f = substrate(x) D = 0. 04; mm = 0. 48; Km = 1. 2; Ki = 22; f = -D+mm*x/(Km+x+x^2/Ki);
Matlab Example #2 cont. l Guess solution and call function fzero >> xo=0; >> fzero('substrate', xo) >> ans = 0. 1091 (meaningful) l Solution obtained depends on initial guess >> xo=10; >> fzero('substrate', xo) >> ans = -20. 7263 (not meaningful)
- Slides: 40