seka Ve skuten velikosti se seka zobraz jen

Úsečka Ve skutečné velikosti se úsečka zobrazí jen tehdy, leží-li v rovině rovnoběžné ( totožné) s průmětnou p nebo n. To znamená, že pokud je půdorys nebo nárys úsečky rovnoběžný s osou x, pak zbývající průmět úsečky je zobrazen ve skutečné velikosti. Skutečná velikost B 2 A 2 X 1, 2 A 1 B 1 Skutečná velikost Z toho plyne, že pokud se nárys nebo půdorys úsečky promítá jako bod, pak druhý průmět této úsečky je zobrazen ve skutečné velikosti. © Kuntová Ivana

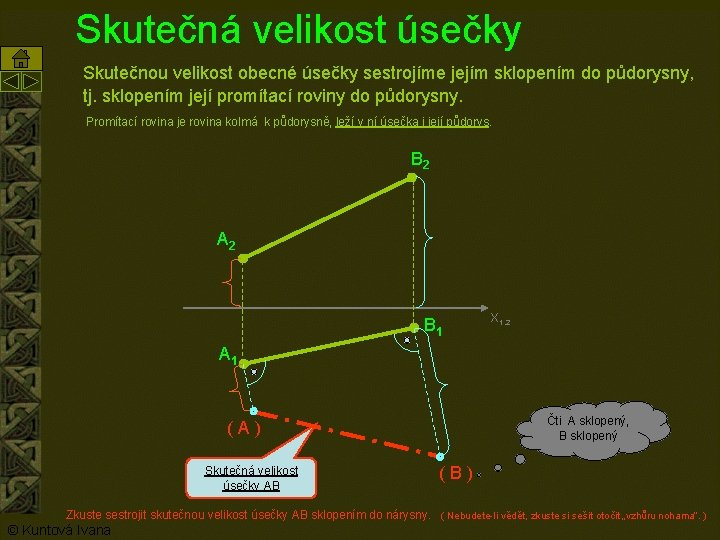
Skutečná velikost úsečky Skutečnou velikost obecné úsečky sestrojíme jejím sklopením do půdorysny, tj. sklopením její promítací roviny do půdorysny. Promítací rovina je rovina kolmá k půdorysně, leží v ní úsečka i její půdorys. B 2 A 2 B 1 X 1, 2 A 1 Čti A sklopený, B sklopený (A) Skutečná velikost úsečky AB (B) Zkuste sestrojit skutečnou velikost úsečky AB sklopením do nárysny. ( Nebudete-li vědět, zkuste si sešit otočit „vzhůru nohama“. ) © Kuntová Ivana

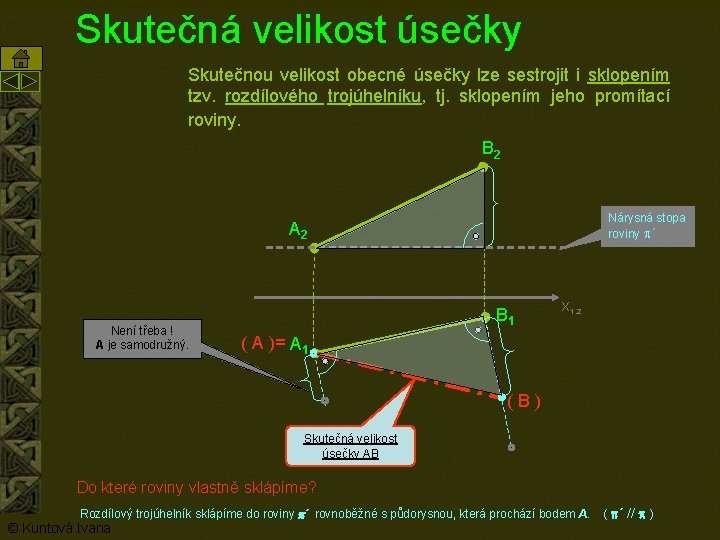
Skutečná velikost úsečky Skutečnou velikost obecné úsečky lze sestrojit i sklopením tzv. rozdílového trojúhelníku, tj. sklopením jeho promítací roviny. B 2 Nárysná stopa roviny p´ A 2 Není třeba ! A je samodružný. B 1 X 1, 2 ( A )= A 1 (B) Skutečná velikost úsečky AB Do které roviny vlastně sklápíme? Rozdílový trojúhelník sklápíme do roviny p´ rovnoběžné s půdorysnou, která prochází bodem A. © Kuntová Ivana ( p´ // p )

Skutečná velikost úsečky Skutečnou velikost obecné úsečky lze sestrojit i jejím otočením do průčelné roviny ( do roviny rovnoběžné s nárysnou ). B 2 =B 2 o Skutečná velikost úsečky AB Osa otáčení A 2 o A 2 X 1, 2 V půdorysu se bod A pohybuje po kružnici, dostaneme otočený půdorys bodu A A 1 o B 1 =B 1 o A 1 V nárysu se pohyb bodu A po kružnici promítne jako pohyb po úsečce. Dostaneme otočený nárys bodu A. Konstrukce je velmi užitečná např. u jehlanů a kuželů s výškou kolmou k půdorysně. © Kuntová Ivana

Skutečná velikost úsečky výpočtem Skutečnou velikost obecné úsečky můžeme vypočítat jako délku tělesové úhlopříčky kvádru s rozměry Dx, Dy, Dz. B 2 Dx = |x. A - x. B | Dz Dy = |y. A - y. B | A 2 Dz = |z. A - z. B | Dx Dy X 1, 2 B 1 | AB | = A 1 Všimněte si, že na volbě umístění osy x 12 nezáleží. Výpočtem rozdílů příslušných souřadnic vlastně posouváme počátek souřadnicových os. Př. : Určete početně i graficky velikost úsečky AB je-li dáno: A[ 2; 3; -3 ], B[ 4; -1; 1 ]. © Kuntová Ivana Početně : | AB | = ( 22+42+42)1/2 = 6