Seismology Part VIII Normal Modes and Free Oscillations








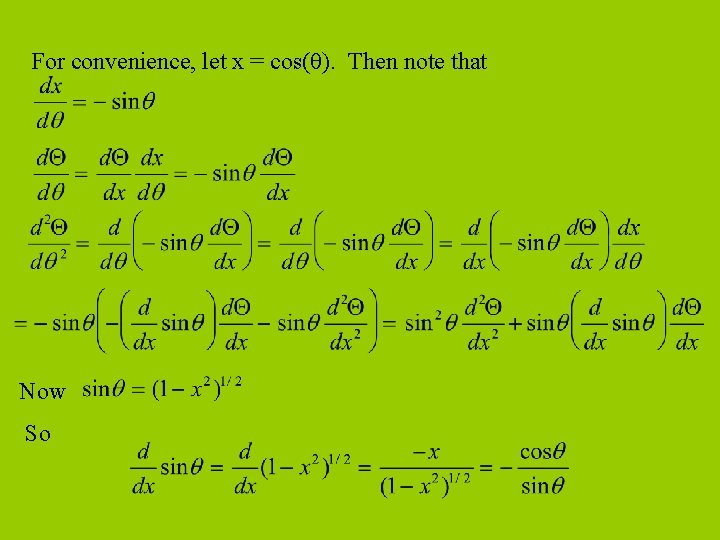
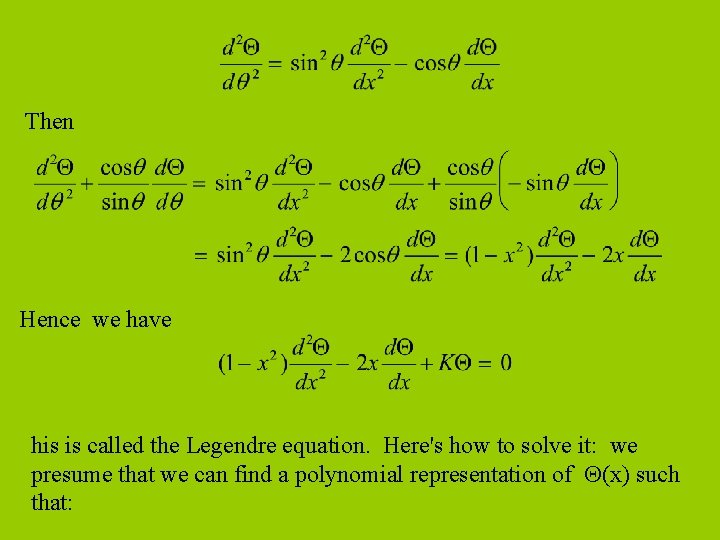
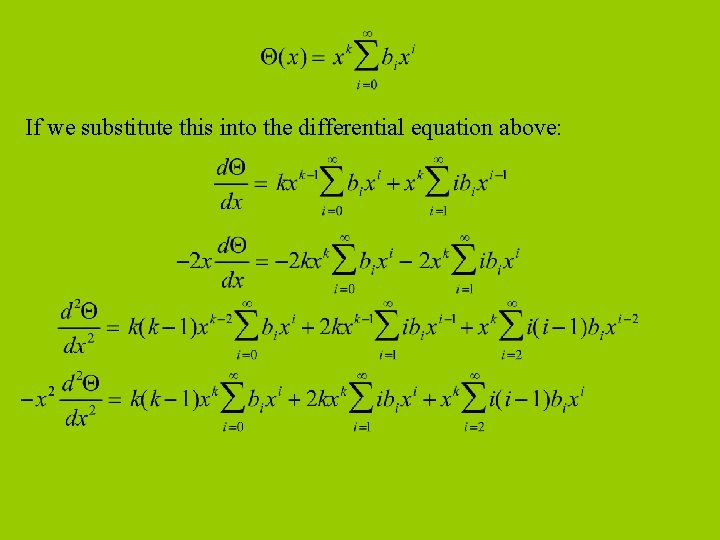









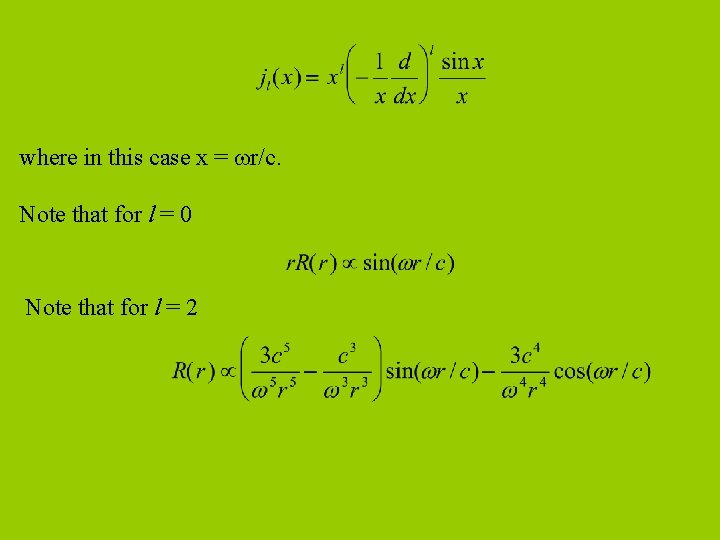




- Slides: 30

Seismology Part VIII: Normal Modes and Free Oscillations

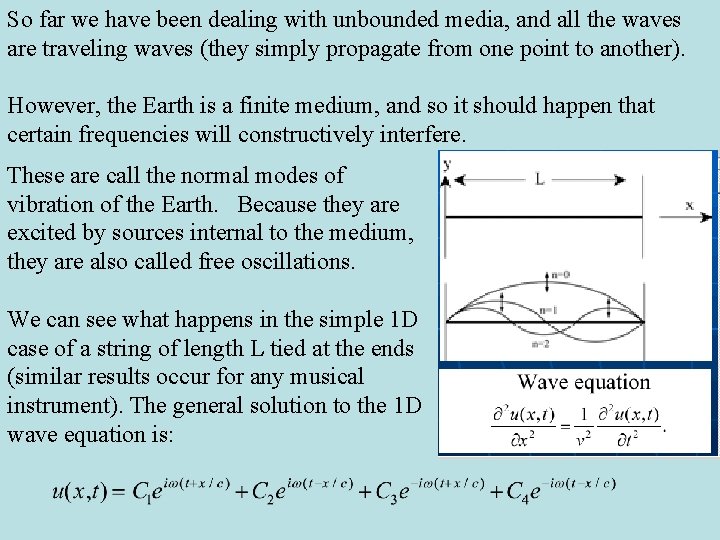
So far we have been dealing with unbounded media, and all the waves are traveling waves (they simply propagate from one point to another). However, the Earth is a finite medium, and so it should happen that certain frequencies will constructively interfere. These are call the normal modes of vibration of the Earth. Because they are excited by sources internal to the medium, they are also called free oscillations. We can see what happens in the simple 1 D case of a string of length L tied at the ends (similar results occur for any musical instrument). The general solution to the 1 D wave equation is:

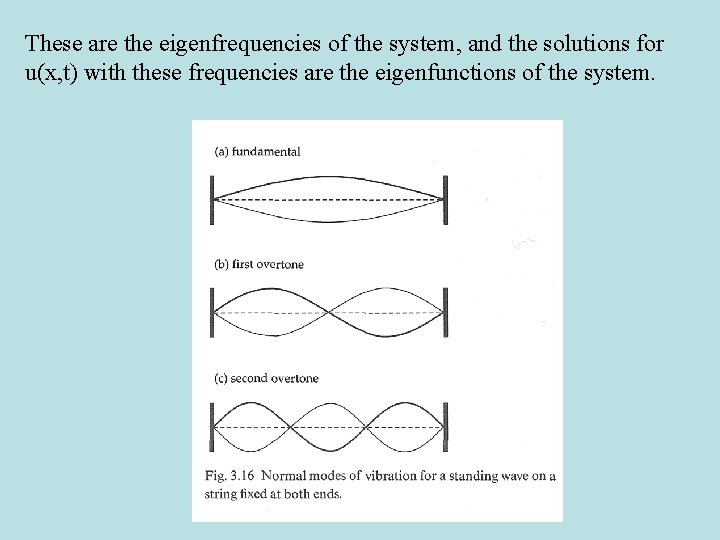
We set the boundary conditions: u(0, t) = u(L, t) = 0. At x=0: and so C 1 = -C 2 and C 3 = -C 4. Then at x=L: Nontrivial solutions are found with the argument to the sine is a multiple of .

These are the eigenfrequencies of the system, and the solutions for u(x, t) with these frequencies are the eigenfunctions of the system.

Note that although this solution seems to be particular to a certain kind of wave (standing wave), in fact we can generate the solution to any arbitrary disturbance (including traveling waves) by summing over properly weighted normal modes: Thus, surface waves that traverse the Earth several times can be thought of as packets of waves moving about the Earth or as eigenfunctions of the Earth’s vibrations. By definition, the normal modes represent ALL of the possible vibrations in the planet (or any body) and so it should in theory be possible to construct any wave by superimposing them.


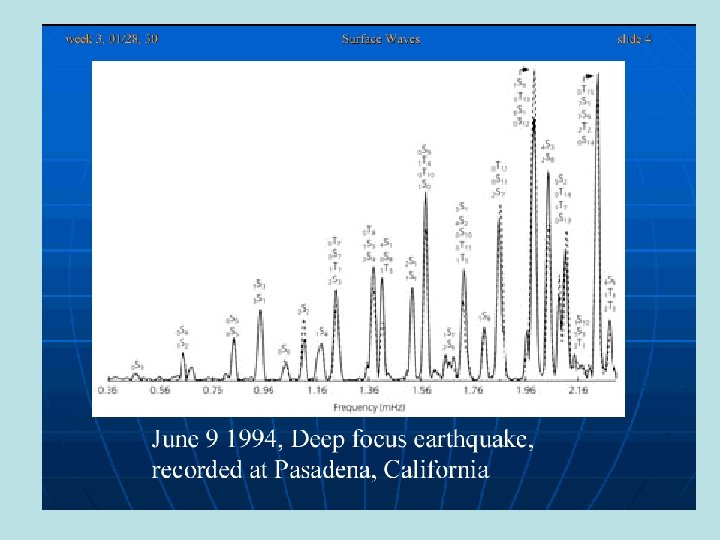
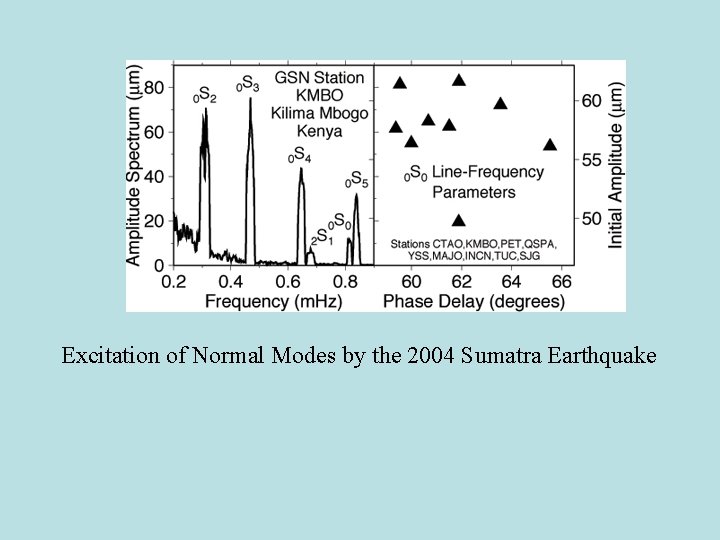
Excitation of Normal Modes by the 2004 Sumatra Earthquake

The best way to think about what happens on a sphere is to view the waves as solutions to the wave equation on terms of spherical harmonics. Let’s consider how this would work for a fluid earth (so only compressional waves). The solid earth case is analogous but there’s a lot more arithmetic involved. First, we have to write the wave equation in a spherical coordinate system (r, instead of (x, y, z): In this case S is the pressure in the fluid (so should be zero at the surface). Note also that our sphere is also non-rotating. (why is that important? )

Solve the above using separation of variables (the usual trick): S(r, t R(r) T(t) We’ll let T(t) = e-i t.

Thus, eliminating T: or The left hand side is independent of , so the right hand side must be a constant. If we choose this to be m 2 then

which has the general solution = eim = cos(m ) + isin(m ) Note that m must be an integer (0, +-1, +-2, etc. ) to preserve the 2 spatial periodicity on a sphere. We now have

Each side must be equal to the same constant. Let's call that K, so that Let's see what happens to the equation when m=0. or
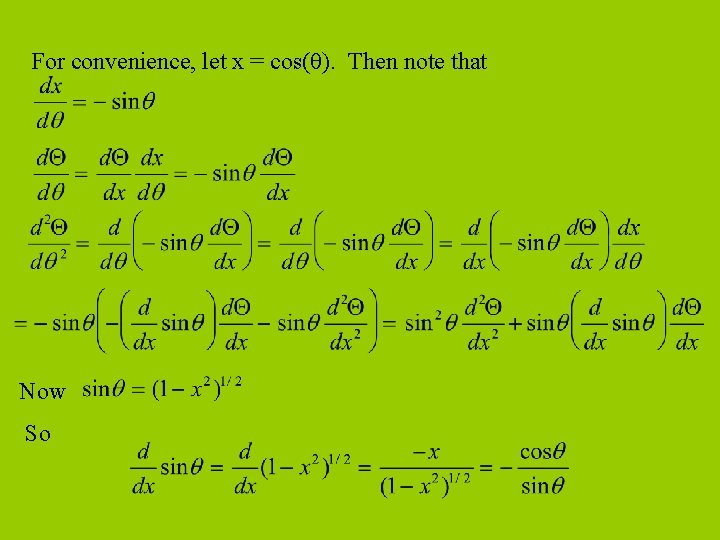
For convenience, let x = cos( ). Then note that Now So
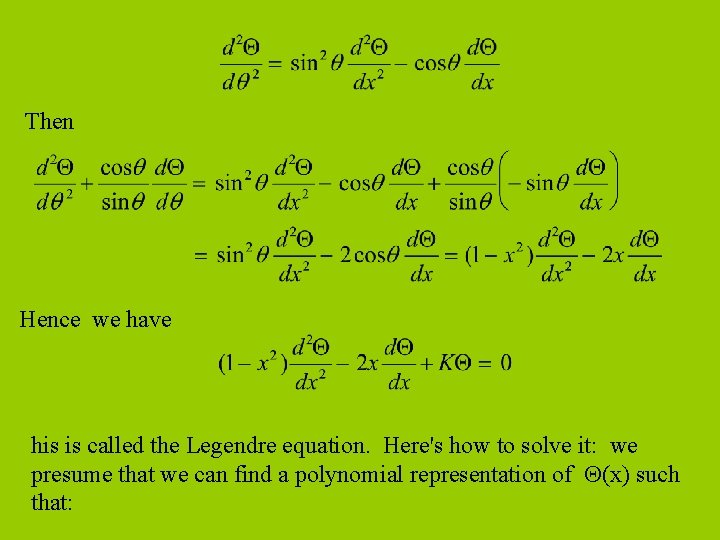
Then Hence we have his is called the Legendre equation. Here's how to solve it: we presume that we can find a polynomial representation of (x) such that:
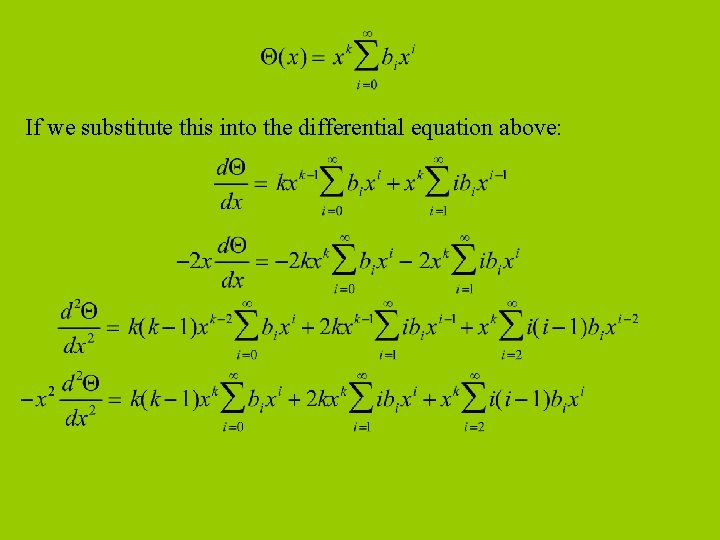
If we substitute this into the differential equation above:

So Identifying equal powers of x in the above gives:

or in general for the xk term: From the first equality, we see that k=0 or k=1. The k=1 solutions are a subset of k=0, so we choose k=0 for the most general case. Thus Note that

so the series will converge as long as -1<x<1 or 0< (i. e. almost everywhere on earth). What about x = 1 or x = -1? It turns out that the polynomial for will diverge unless by some chance an even suffix bi and an odd suffix bi is zero, which of course means that the sum is no longer infinite (so convergence is guaranteed - duh). Looking above at the definition of b, we see that any bi+2 will be equal to zero for a nonzero bi only if K = (i)(i+1). Thus, it must be that K is the product of two successive integers! Let K = l(l+1). Then If l is even then it is a sequence of even suffixed b that make up the solution and we must require that b 1 = 0 (so all odd guys are zero). Similarly , if l is odd then the sequence is odd-suffix bi and b 0 = 0. In either case, is a polynomial of order l.

Typically, we choose bo or b 1 by requiring (x) = 1 for x = 1 (i. e. , = 0 degrees). The resulting polynomials are called Legendre polynomials, and they have the general form: stopping with either x or 1(times a constant) as the last term. The first few polynomials are:

They can also be calculated using Rodrigues' formula: Ok, so how about when m is not 0? In this case, our substitution trick gives: It turns out that the polynomial approach above bogs down, and the way to solve this guy is to look at what happens when x gets close to +-1. We also factor such that:

and determine that A(x) satisfies the ODE: This equation can be expanded just like we did before: and we get a similar recursive relationship for c: Note that when m=0 we revert to our equation for bi. As before: ci+2 = 0 for some i, and additionally if c has an even index, then we require that c 1 = 0, and if c has an odd index, then c 0 = 0. Thus, K has the eigenvalues:

or again that K is the product of consecutive integers. If we let l = i + m as before, then because i > 0 it must be that m < l. Thus, there is an constraining relation between the order of the solution for Q and the latitudinal order m. However, note that K can have the same eigenvalues for different choices of m, so there is some independence. If we differentiate the original Legendre polynomial equation m times we get:

which looks just like the equation for A(x), where we identify A(x) as the mth derivative of Pl. Thus: These mth derivatives of the Legendre polynomials are called associated Legendre functions. From the Rodrigues formula above, we see that which is valid for all l and all m such that -l<m<l.

We often combine the solutions for and (along with a normalization factor) to produce the function: Now, let's get an expression for R(r). Substituting our value of K in the above gives: is a form of the Bessel equation, which has solutions called spherical Bessel functions or Hankel functions of the form:
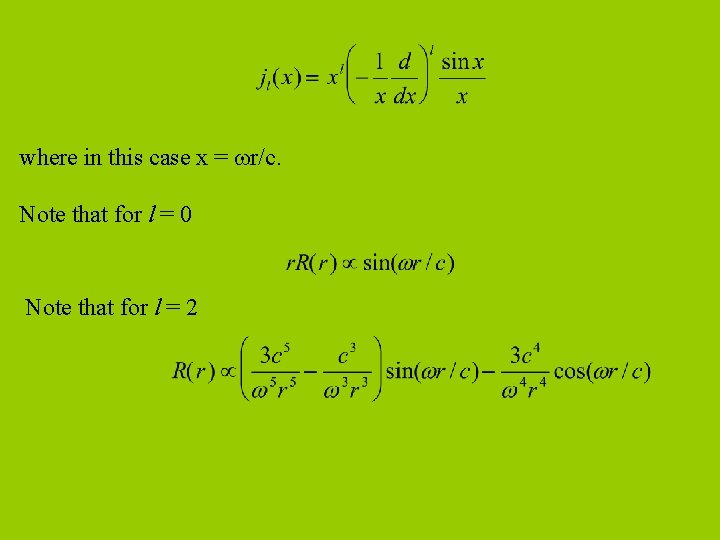
where in this case x = r/c. Note that for l = 0 Note that for l = 2

Because this is a pressure wave (the wave equation is posed with pressure as the variable), the free surface condition is that R(ro) = 0. Thus for l = 0 it must be that: from which the eigenfrequencies n l for this case are: where n = 0 is the fundamental mode and n > 0 are the overtones. Note that for any choice of l (and mode n), because -l < m < l, there are 2 l-1 possible choices of m that go with the same eigenfrequency. Thus, a single frequency will correspond to several different free oscillations. This is referred to as frequency degeneracy.

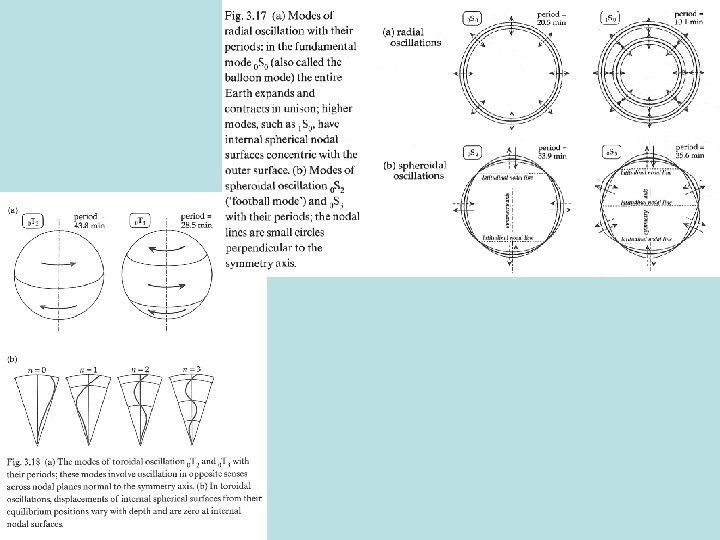
Note that l = 0 is a purely radial mode, because the associated and motions are zero. In a sphere, we have to concern ourselves with two basic kinds of vibration: Spheroidal: involving motion in the radial direction Toroidal: motion parallel to the surface. There is a useful nomenclature developed to classify the different spherical modes: n. S l n. T l The index on the left indicates the number of zero crossings.

The index on the right indicates the angular order or degree of the harmonic. A node at the surface will appear every /n degrees, or equivalently motion of the same type will appear every 2 /n degrees. Some examples: The whole Earth expanding and contracting. At every 0 S 0 point the radius is increasing and decreasing in phase. 1 S 0 Imagine the same picture as 0 S 0, but the inner part of the Earth is contracting while the outer half is expanding. 0 S 1 Would be one half of the Earth contracting while the other half is expanding. This would result in a net change in the center of mass of the Earth, and hence cannot be excited by an internal source. 0 S 2 is sometimes called the “football” mode. Imagine the Earth compressing at the poles and expanding at the equator

0 T 0 Undefined – can’t work because toroidal modes by definition have to repeat every 2 0 T 1 Nonphysical – would cause the earth’s rotation to increase and decrease, which would violate conservation of angular momentum 0 T 2 One hemisphere twists in one direction; other hemisphere in opposite direction. Depth sensitivity: Generally complicated, but fundamental modes have energy concentrated in the upper mantle. Splitting: Caused mostly by rotation (Coriollis and angular momentum). Multiplets split into singlets.

 Elasticity and oscillations
Elasticity and oscillations Electromagnetic oscillations and alternating current
Electromagnetic oscillations and alternating current Electromagnetic oscillation pdf
Electromagnetic oscillation pdf Seismology timeline
Seismology timeline Focal mechanism beach ball
Focal mechanism beach ball Orfeus seismology
Orfeus seismology Seismology nepal
Seismology nepal Seismology
Seismology Beach ball earthquake
Beach ball earthquake Seismology
Seismology Whats seismology
Whats seismology Elements of seismology
Elements of seismology Seismology
Seismology Seismology
Seismology Seismology
Seismology Baryon acoustic oscillations
Baryon acoustic oscillations Graded oscillation techniques
Graded oscillation techniques Baryon acoustic oscillations
Baryon acoustic oscillations Baryon acoustic oscillations
Baryon acoustic oscillations Baryon acoustic oscillations
Baryon acoustic oscillations Baryonic acoustic oscillations
Baryonic acoustic oscillations Coupled oscillations
Coupled oscillations Slow oscillations
Slow oscillations Coupled oscillations
Coupled oscillations Electrical conductivity formula
Electrical conductivity formula Plasma oscillations
Plasma oscillations Lotka-volterra predator-prey model
Lotka-volterra predator-prey model Code of ethics article 4
Code of ethics article 4 Luther calvin and henry viii
Luther calvin and henry viii Luther calvin and henry viii
Luther calvin and henry viii Helmholtz free energy and gibbs free energy
Helmholtz free energy and gibbs free energy