Seismic Thickness Estimation Three Approaches Pros and Cons


















- Slides: 45

Seismic Thickness Estimation: Three Approaches, Pros and Cons Gregory A. Partyka bp

Outline • Introduction • Three Approaches • Examples • Pros and Cons

Outline • Introduction • Three Approaches • Examples • Pros and Cons

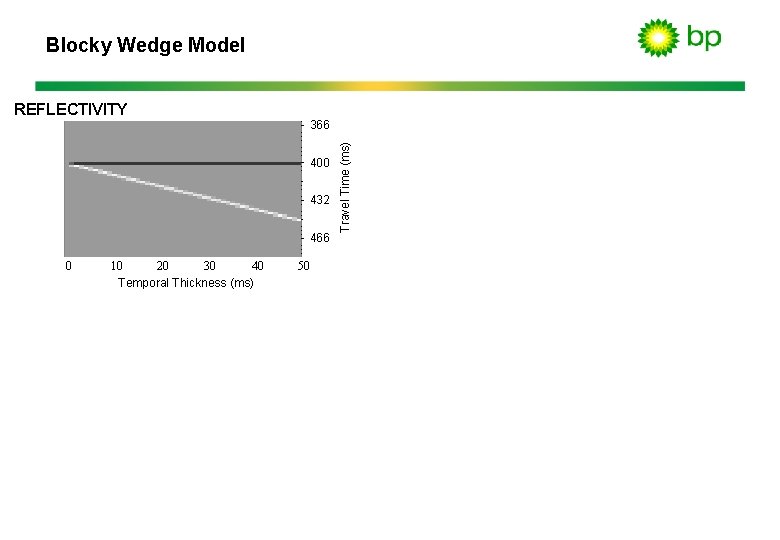
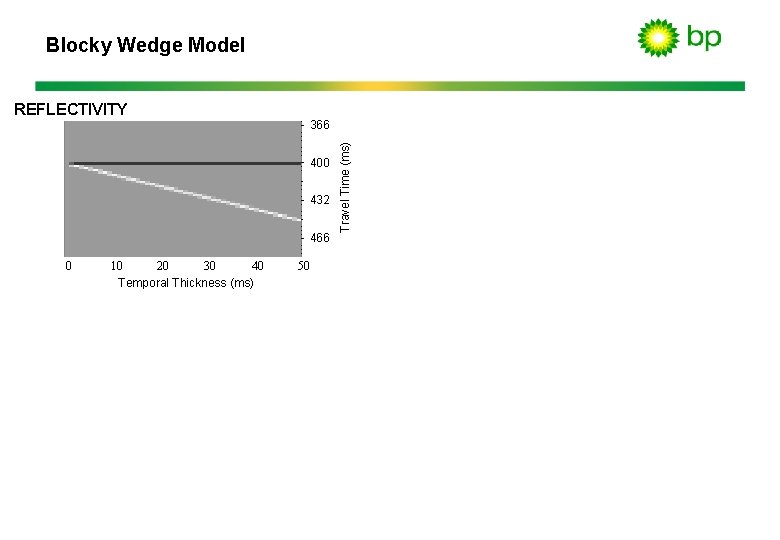
Blocky Wedge Model 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) 50 Travel Time (ms) REFLECTIVITY

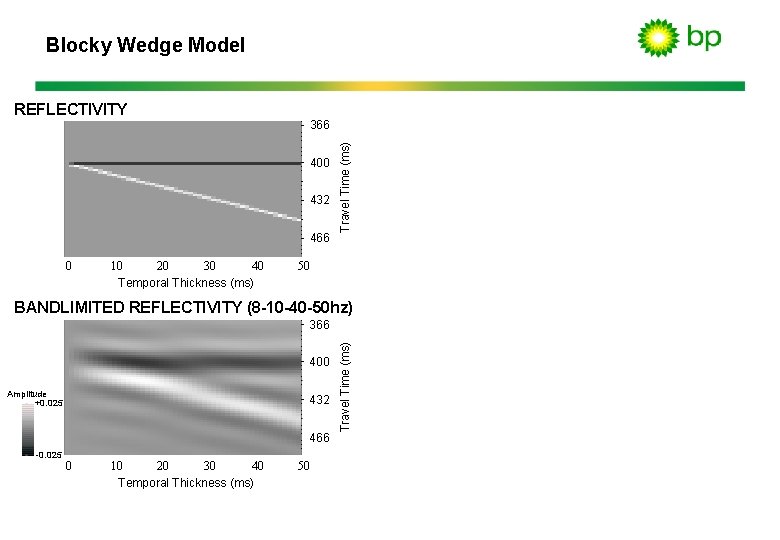
Blocky Wedge Model 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) Travel Time (ms) REFLECTIVITY 50 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 -0. 025 0 40 10 20 30 Temporal Thickness (ms) 50 Travel Time (ms) 366

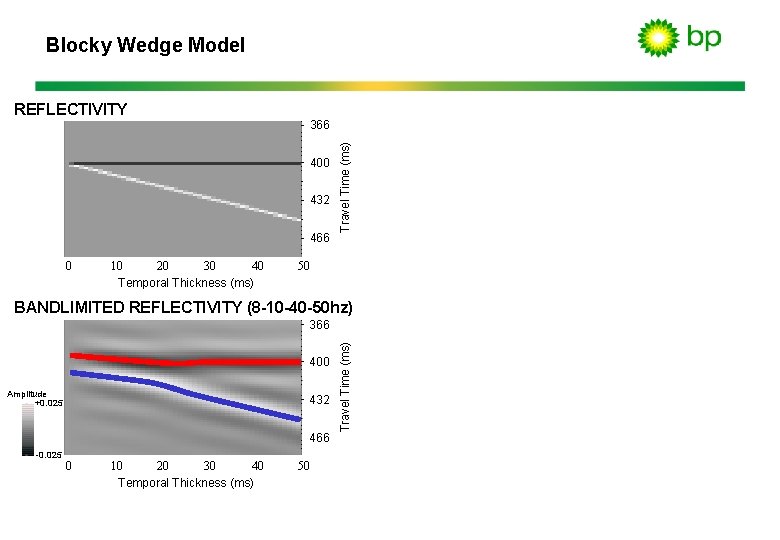
Blocky Wedge Model 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) Travel Time (ms) REFLECTIVITY 50 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 -0. 025 0 40 10 20 30 Temporal Thickness (ms) 50 Travel Time (ms) 366

Outline • Introduction • Three Approaches • Examples • Pros and Cons

Three Approaches to Thickness Estimation 1. Conventional • peak-trough time separation • amplitude 2. Spectral Decomposition • 1 st dominant frequency and amplitude 3. Spectral Decomposition • discrete frequency components

Three Approaches to Thickness Estimation 1. Conventional • peak-trough time separation • amplitude 2. Spectral Decomposition • 1 st dominant frequency and amplitude 3. Spectral Decomposition • discrete frequency components

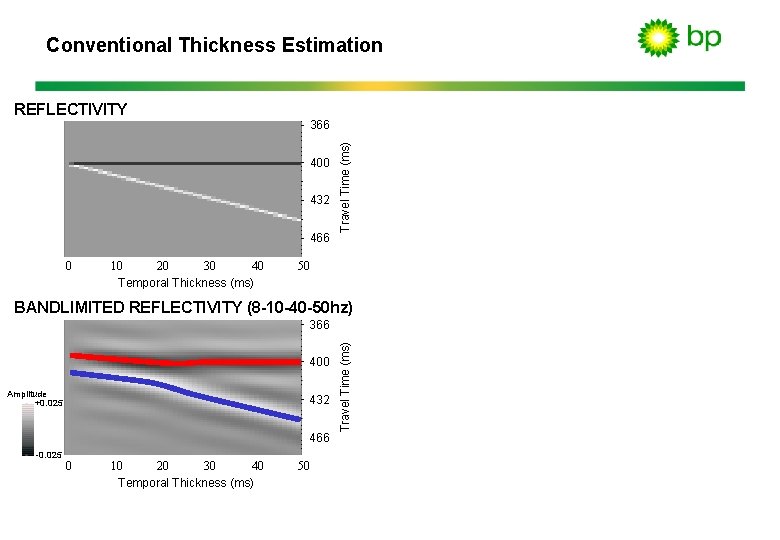
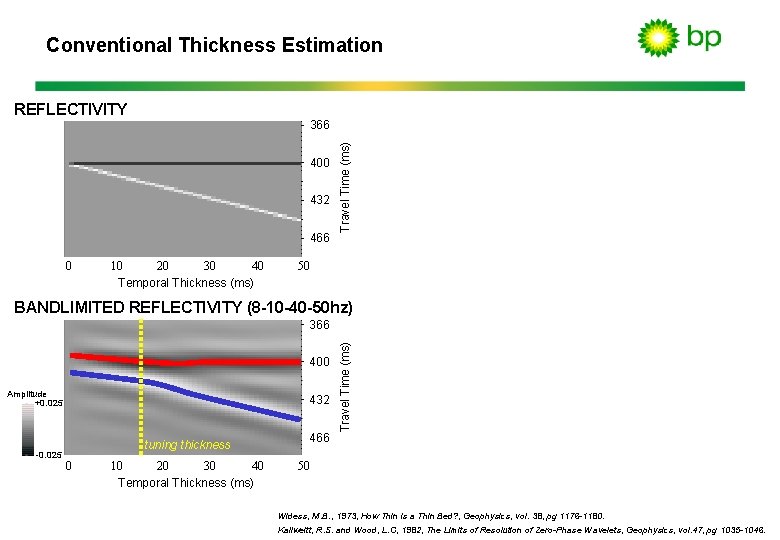
Conventional Thickness Estimation 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) Travel Time (ms) REFLECTIVITY 50 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 -0. 025 0 40 10 20 30 Temporal Thickness (ms) 50 Travel Time (ms) 366

Conventional Thickness Estimation REFLECTIVITY 400 432 466 0 40 10 20 30 Temporal Thickness (ms) Travel Time (ms) 366 50 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 -0. 025 432 tuning thickness 0 40 10 20 30 Temporal Thickness (ms) 466 Travel Time (ms) 366 50 Widess, M. B. , 1973, How Thin is a Thin Bed? , Geophysics, vol. 38, pg 1176 -1180. Kallweitt, R. S. and Wood, L. C, 1982, The Limits of Resolution of Zero-Phase Wavelets, Geophysics, vol. 47, pg 1035 -1046.

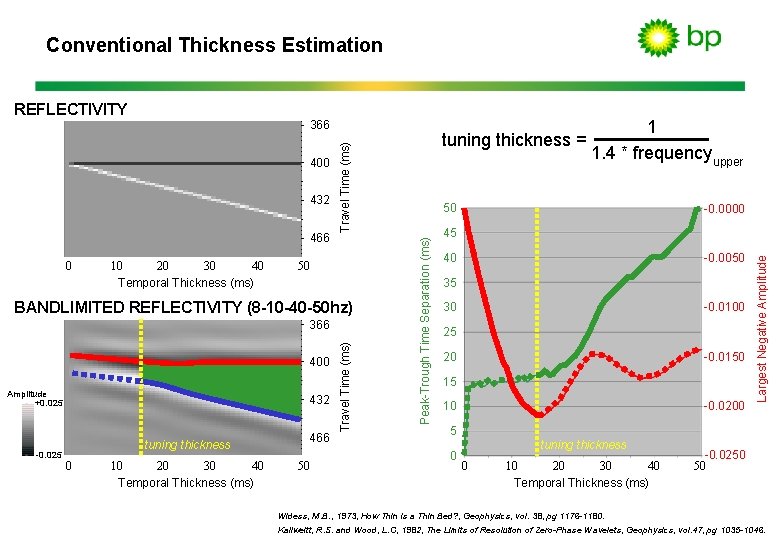
Conventional Thickness Estimation 366 466 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 -0. 025 432 tuning thickness 0 40 10 20 30 Temporal Thickness (ms) 466 50 Travel Time (ms) 366 1 1. 4 * frequency upper 50 Peak-Trough Time Separation (ms) 432 Travel Time (ms) 400 tuning thickness = -0. 0000 45 40 -0. 0050 35 -0. 0100 30 25 20 -0. 0150 15 -0. 0200 10 Largest Negative Amplitude REFLECTIVITY 5 0 tuning thickness 0 40 10 20 30 Temporal Thickness (ms) -0. 0250 50 Widess, M. B. , 1973, How Thin is a Thin Bed? , Geophysics, vol. 38, pg 1176 -1180. Kallweitt, R. S. and Wood, L. C, 1982, The Limits of Resolution of Zero-Phase Wavelets, Geophysics, vol. 47, pg 1035 -1046.

Three Approaches to Thickness Estimation 1. Conventional • peak-trough time separation • amplitude 2. Spectral Decomposition • 1 st dominant frequency and amplitude 3. Spectral Decomposition • discrete frequency components

Spectral Decomposition • uses the discrete Fourier transform to: – quantify thin-bed interference, and – detect subtle discontinuities.

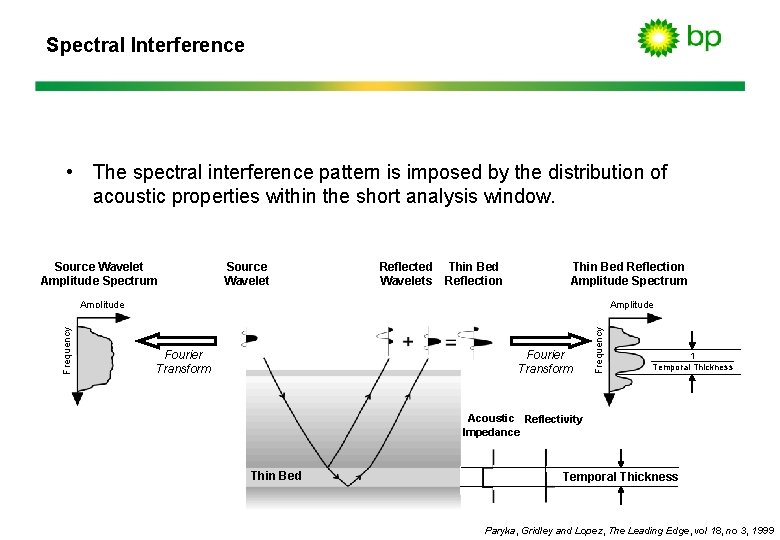
Spectral Interference • The spectral interference pattern is imposed by the distribution of acoustic properties within the short analysis window. Source Wavelet Amplitude Spectrum Source Wavelet Reflected Thin Bed Wavelets Reflection Thin Bed Reflection Amplitude Spectrum Amplitude Fourier Transform Frequency Amplitude 1 Temporal Thickness Acoustic Reflectivity Impedance Thin Bed Temporal Thickness Paryka, Gridley and Lopez, The Leading Edge, vol 18, no 3, 1999

Blocky Wedge Model 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) 50 Travel Time (ms) REFLECTIVITY

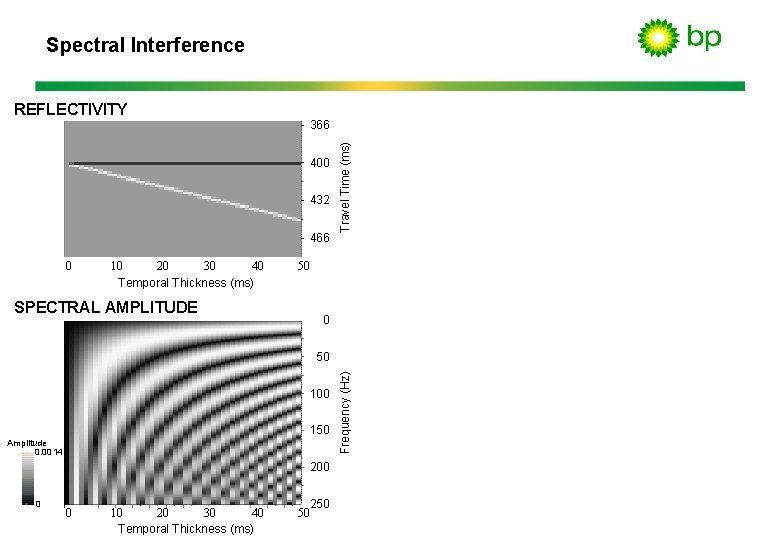
Spectral Interference 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) SPECTRAL AMPLITUDE Travel Time (ms) REFLECTIVITY 50 0 100 150 Amplitude 0. 0014 200 0 0 40 10 20 30 Temporal Thickness (ms) 250 50 Frequency (Hz) 50

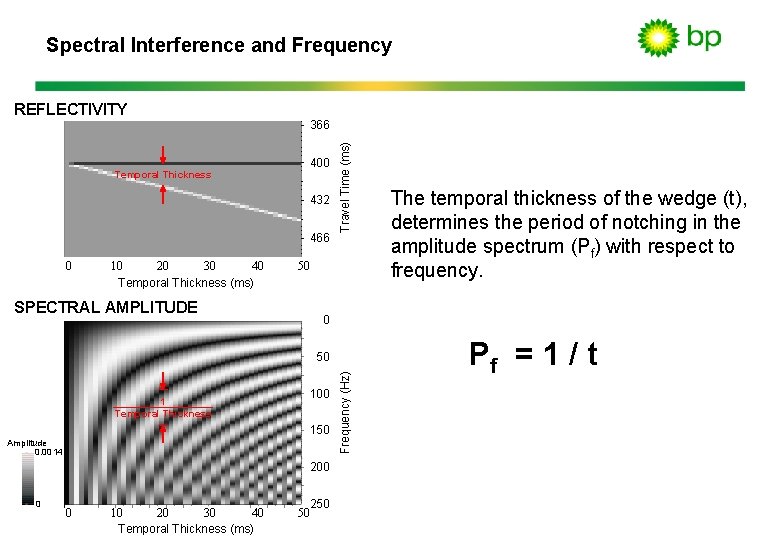
Spectral Interference and Frequency Temporal Thickness 366 400 432 466 0 40 10 20 30 Temporal Thickness (ms) SPECTRAL AMPLITUDE Travel Time (ms) REFLECTIVITY 50 0 100 150 Amplitude 0. 0014 200 0 0 40 10 20 30 Temporal Thickness (ms) 250 50 Frequency (Hz) 50 1 Temporal Thickness The temporal thickness of the wedge (t), determines the period of notching in the amplitude spectrum (Pf) with respect to frequency. Pf = 1 / t

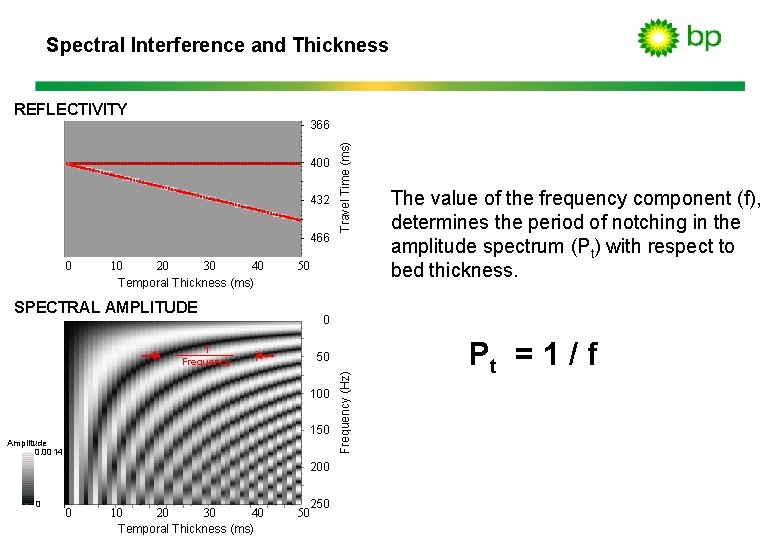
Spectral Interference and Thickness REFLECTIVITY 400 432 466 40 10 20 30 Temporal Thickness (ms) SPECTRAL AMPLITUDE 1 Frequency 50 50 100 150 Amplitude 0. 0014 200 0 0 40 10 20 30 Temporal Thickness (ms) The value of the frequency component (f), determines the period of notching in the amplitude spectrum (Pt) with respect to bed thickness. 0 250 50 Frequency (Hz) 0 Travel Time (ms) 366 Pt = 1 / f

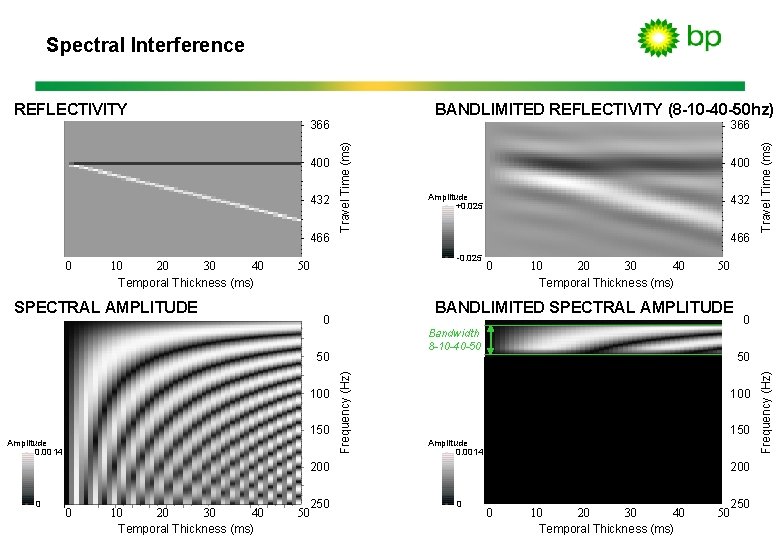
Spectral Interference 466 40 10 20 30 Temporal Thickness (ms) SPECTRAL AMPLITUDE 400 Amplitude +0. 025 466 -0. 025 50 Frequency (Hz) 150 40 10 20 30 Temporal Thickness (ms) Bandwidth 8 -10 -40 -50 50 Amplitude 0. 0014 0 0 40 10 20 30 Temporal Thickness (ms) 250 50 100 150 Amplitude 0. 0014 200 0 50 BANDLIMITED SPECTRAL AMPLITUDE 0 100 432 200 0 Travel Time (ms) 432 366 0 40 10 20 30 Temporal Thickness (ms) 250 50 Frequency (Hz) 366 400 0 BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) Travel Time (ms) REFLECTIVITY

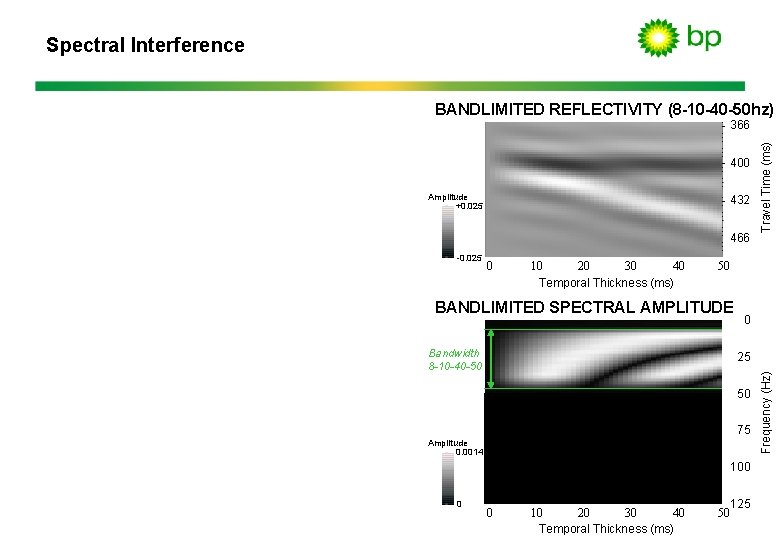
Spectral Interference BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE Bandwidth 8 -10 -40 -50 0 25 50 75 Amplitude 0. 0014 100 0 0 40 10 20 30 Temporal Thickness (ms) 125 50 Frequency (Hz) -0. 025 Travel Time (ms) 366

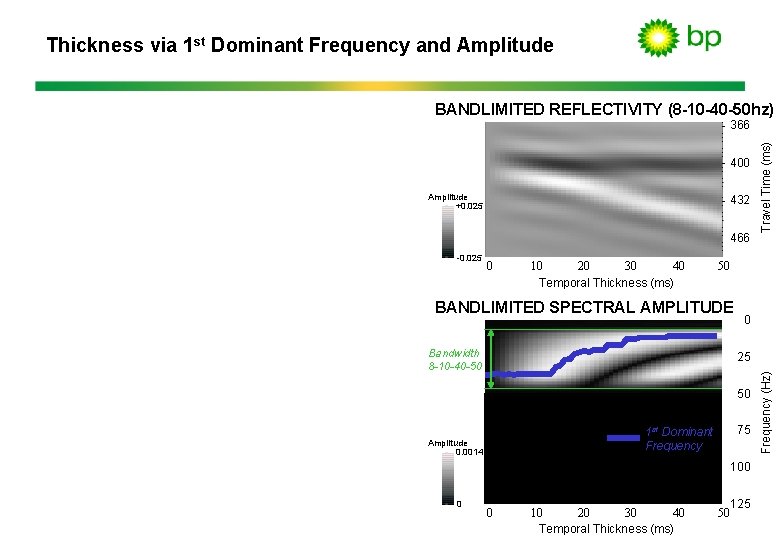
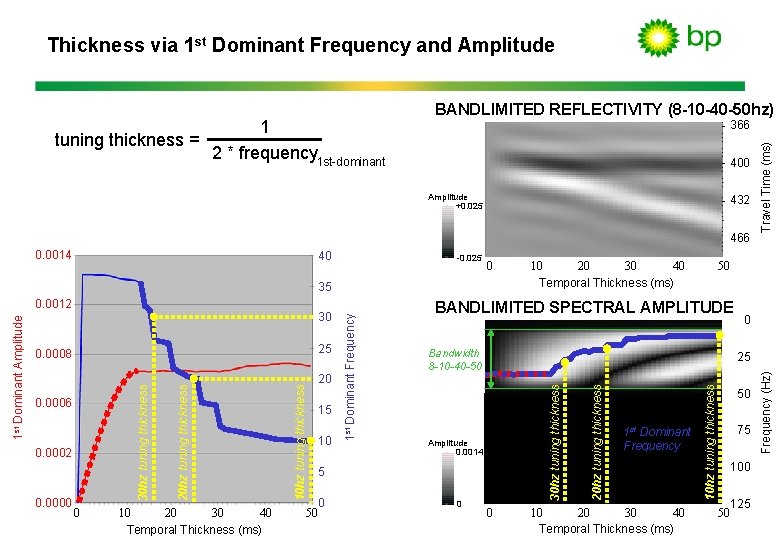
Thickness via 1 st Dominant Frequency and Amplitude BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE Bandwidth 8 -10 -40 -50 0 25 50 1 st Dominant Frequency Amplitude 0. 0014 75 100 0 0 40 10 20 30 Temporal Thickness (ms) 125 50 Frequency (Hz) -0. 025 Travel Time (ms) 366

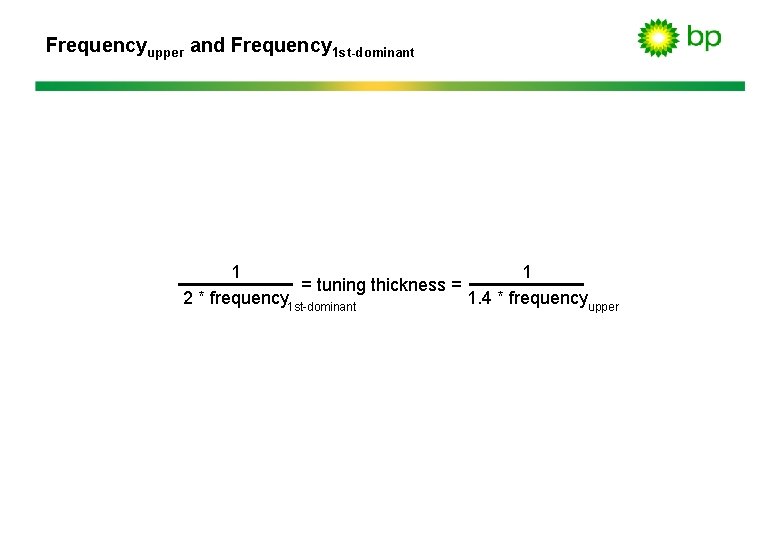
Frequencyupper and Frequency 1 st-dominant 1 1 = tuning thickness = 1. 4 * frequency upper 2 * frequency 1 st-dominant

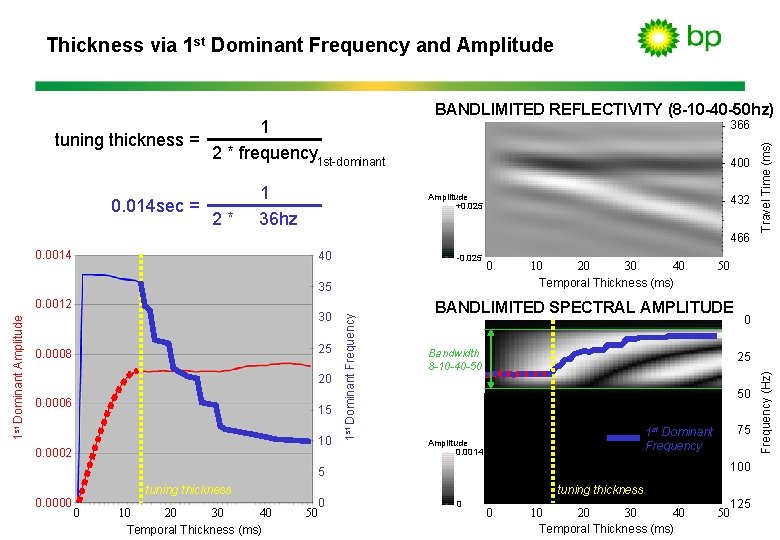
Thickness via 1 st Dominant Frequency and Amplitude 2* 400 Amplitude +0. 025 432 466 0. 0014 40 -0. 025 0 1 st Dominant Amplitude 0. 0012 30 25 0. 0008 20 0. 0006 15 10 0. 0002 1 st Dominant Frequency 35 40 10 20 30 Temporal Thickness (ms) tuning thickness 0 40 10 20 30 Temporal Thickness (ms) 50 0 0 25 50 1 st Dominant Frequency Amplitude 0. 0014 75 100 5 0. 0000 50 BANDLIMITED SPECTRAL AMPLITUDE Bandwidth 8 -10 -40 -50 tuning thickness 0 Travel Time (ms) 0. 014 sec = 1 36 hz 366 0 40 10 20 30 Temporal Thickness (ms) 125 50 Frequency (Hz) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

Three Approaches to Thickness Estimation 1. Conventional • peak-trough time separation • amplitude 2. Spectral Decomposition • 1 st dominant frequency and amplitude 3. Spectral Decomposition • discrete frequency components

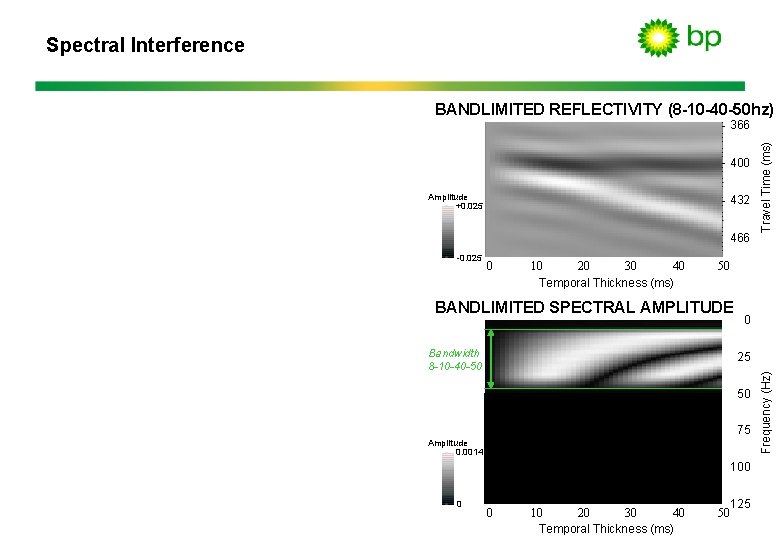
Spectral Interference BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE Bandwidth 8 -10 -40 -50 0 25 50 75 Amplitude 0. 0014 100 0 0 40 10 20 30 Temporal Thickness (ms) 125 50 Frequency (Hz) -0. 025 Travel Time (ms) 366

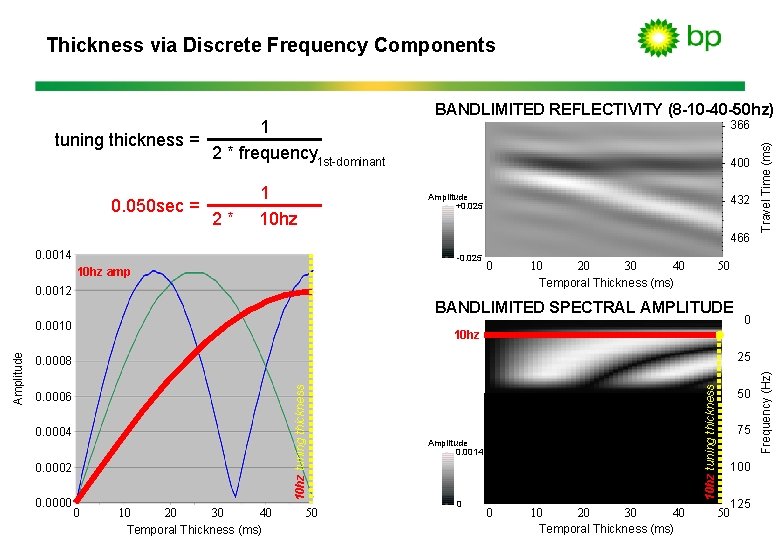
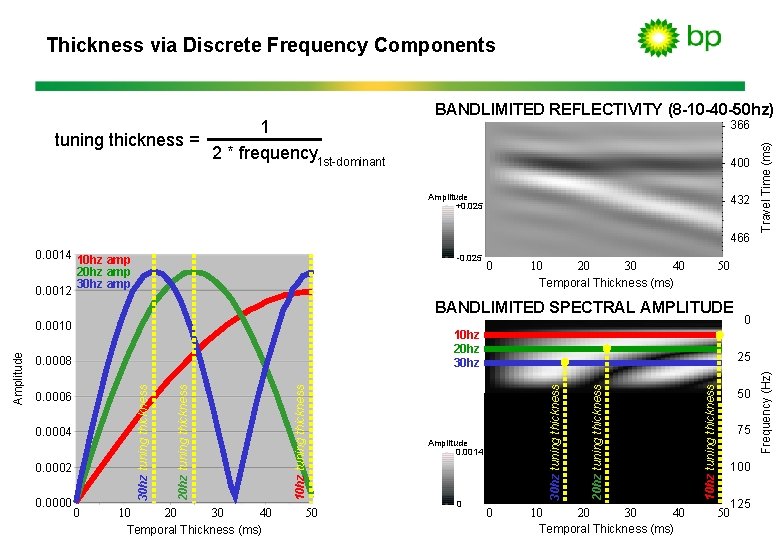
Thickness via Discrete Frequency Components 0. 050 sec = 2* 1 10 hz 366 400 Amplitude +0. 025 432 466 0. 0014 -0. 025 10 hz amp 0 0. 0012 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE 0. 0004 0. 0002 0 40 10 20 30 Temporal Thickness (ms) 50 10 hz tuning thickness 0. 0006 Amplitude 0. 0014 0 0 40 10 20 30 Temporal Thickness (ms) 50 75 100 125 50 Frequency (Hz) 25 0. 0008 0. 0000 0 10 hz tuning thickness Amplitude 0. 0010 Travel Time (ms) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

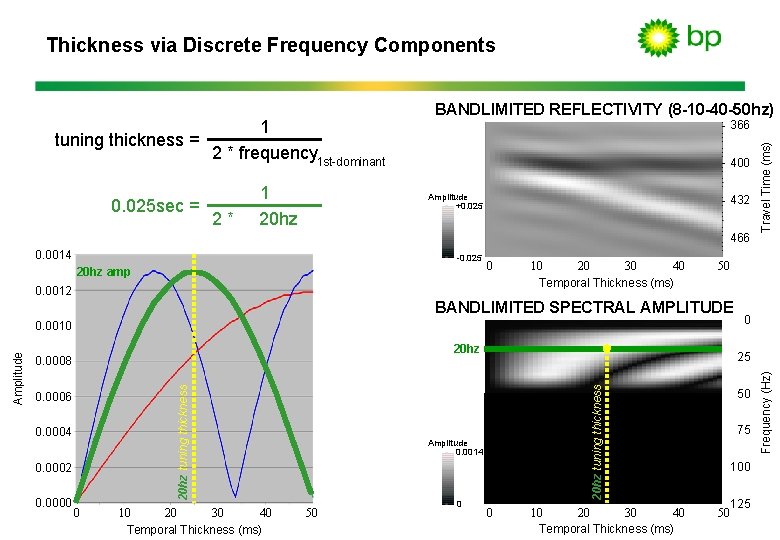
Thickness via Discrete Frequency Components 2* 400 Amplitude +0. 025 432 466 0. 0014 -0. 025 20 hz amp 0 0. 0012 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE 20 hz 0. 0006 0. 0004 0. 0002 0. 0000 0 40 10 20 30 Temporal Thickness (ms) Amplitude 0. 0014 50 0 0 25 20 hz tuning thickness 0. 0008 20 hz tuning thickness Amplitude 0. 0010 Travel Time (ms) 0. 025 sec = 1 20 hz 366 0 40 10 20 30 Temporal Thickness (ms) 50 75 100 125 50 Frequency (Hz) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

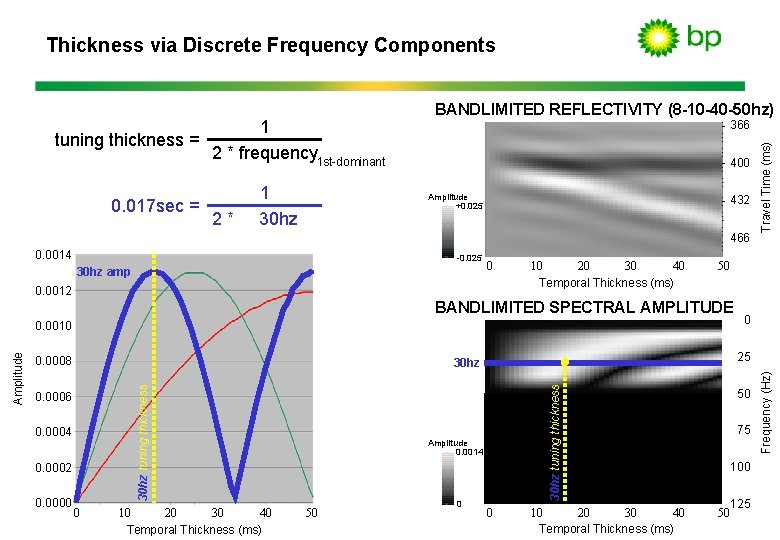
Thickness via Discrete Frequency Components 2* 400 Amplitude +0. 025 432 466 0. 0014 -0. 025 30 hz amp 0 0. 0012 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE 0. 0008 0. 0004 0. 0002 0. 0000 0 40 10 20 30 Temporal Thickness (ms) 30 hz tuning thickness 0. 0006 Amplitude 0. 0014 50 0 0 25 30 hz tuning thickness Amplitude 0. 0010 Travel Time (ms) 0. 017 sec = 1 30 hz 366 0 40 10 20 30 Temporal Thickness (ms) 50 75 100 125 50 Frequency (Hz) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

Thickness via Discrete Frequency Components 400 Amplitude +0. 025 432 466 0. 0014 10 hz amp 20 hz amp 30 hz amp 0. 0012 -0. 025 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE 10 hz 20 hz 30 hz 0 40 10 20 30 Temporal Thickness (ms) 50 0 0 40 10 20 30 Temporal Thickness (ms) 10 hz tuning thickness 0. 0000 Amplitude 0. 0014 20 hz tuning thickness 0. 0002 0 25 30 hz tuning thickness 0. 0004 10 hz tuning thickness 0. 0006 20 hz tuning thickness 0. 0008 30 hz tuning thickness Amplitude 0. 0010 Travel Time (ms) 366 50 75 100 125 50 Frequency (Hz) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

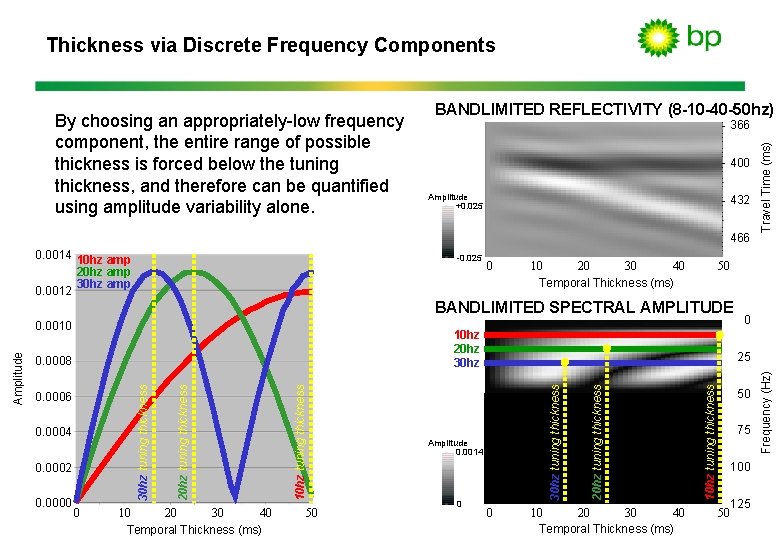
Thickness via Discrete Frequency Components BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz) 400 Amplitude +0. 025 432 466 0. 0014 10 hz amp 20 hz amp 30 hz amp 0. 0012 -0. 025 0 40 10 20 30 Temporal Thickness (ms) 50 BANDLIMITED SPECTRAL AMPLITUDE 10 hz 20 hz 30 hz 0 40 10 20 30 Temporal Thickness (ms) 50 0 0 40 10 20 30 Temporal Thickness (ms) 10 hz tuning thickness 0. 0000 Amplitude 0. 0014 20 hz tuning thickness 0. 0002 0 25 30 hz tuning thickness 0. 0004 10 hz tuning thickness 0. 0006 20 hz tuning thickness 0. 0008 30 hz tuning thickness Amplitude 0. 0010 Travel Time (ms) 366 50 75 100 125 50 Frequency (Hz) By choosing an appropriately-low frequency component, the entire range of possible thickness is forced below the tuning thickness, and therefore can be quantified using amplitude variability alone.

Thickness via 1 st Dominant Frequency and Amplitude 400 Amplitude +0. 025 432 466 -0. 025 0. 0002 0. 0000 0 40 10 20 30 Temporal Thickness (ms) 10 hz tuning thickness 0. 0006 20 hz tuning thickness 0. 0008 50 20 15 10 Bandwidth 8 -10 -40 -50 Amplitude 0. 0014 0 0 25 5 0 50 BANDLIMITED SPECTRAL AMPLITUDE 30 hz tuning thickness 30 30 hz tuning thickness 1 st Dominant Amplitude 0. 0012 1 st Dominant Frequency 35 40 10 20 30 Temporal Thickness (ms) 0 1 st Dominant Frequency 40 10 20 30 Temporal Thickness (ms) 10 hz tuning thickness 40 20 hz tuning thickness 0. 0014 Travel Time (ms) 366 50 75 100 125 50 Frequency (Hz) 1 tuning thickness = 2 * frequency 1 st-dominant BANDLIMITED REFLECTIVITY (8 -10 -40 -50 hz)

Outline • Introduction • Three Approaches • Examples • Pros and Cons

Example • Using discrete frequency components to determine relative thickening/thinning.


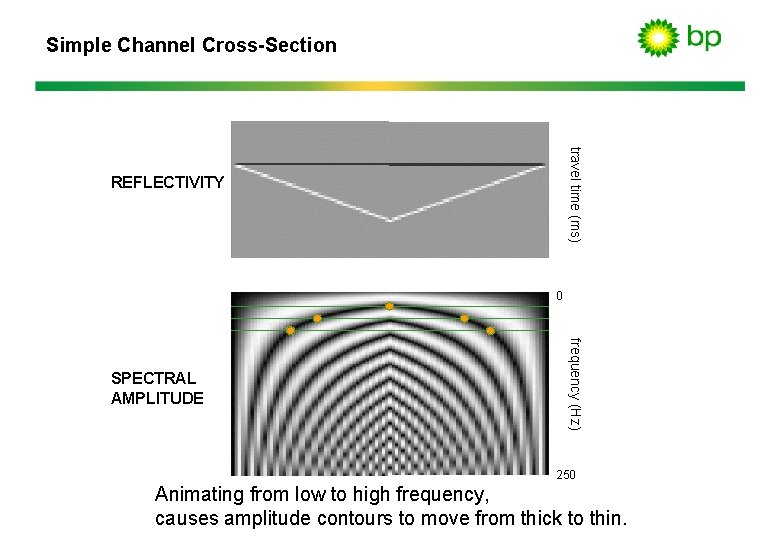
Simple Channel Cross-Section travel time (ms) REFLECTIVITY 0 frequency (Hz) SPECTRAL AMPLITUDE 250 Animating from low to high frequency, causes amplitude contours to move from thick to thin.

Example • Using discrete frequency components to calibrate reservoir thickness.

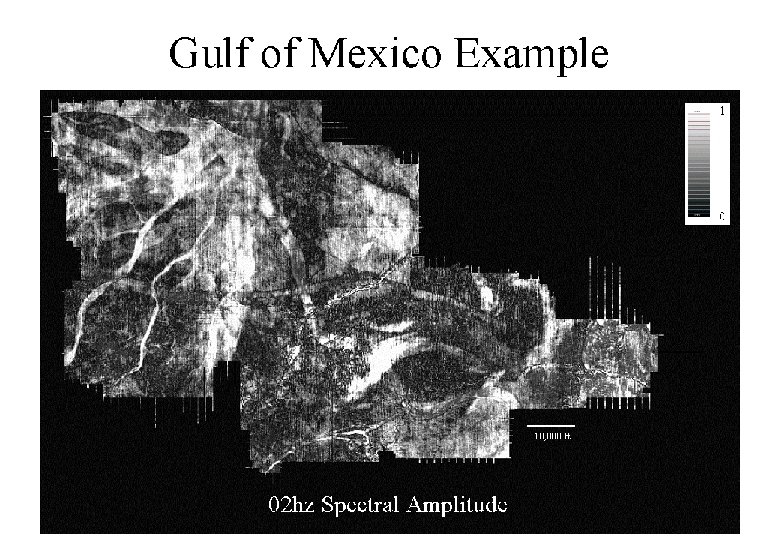
Deep-Water Gulf of Mexico 8 hz Spectral Amplitude Map Zone 1 WELL #1 1 mile Partyka, Thomas, Turco and Hartmann, SEG 2000

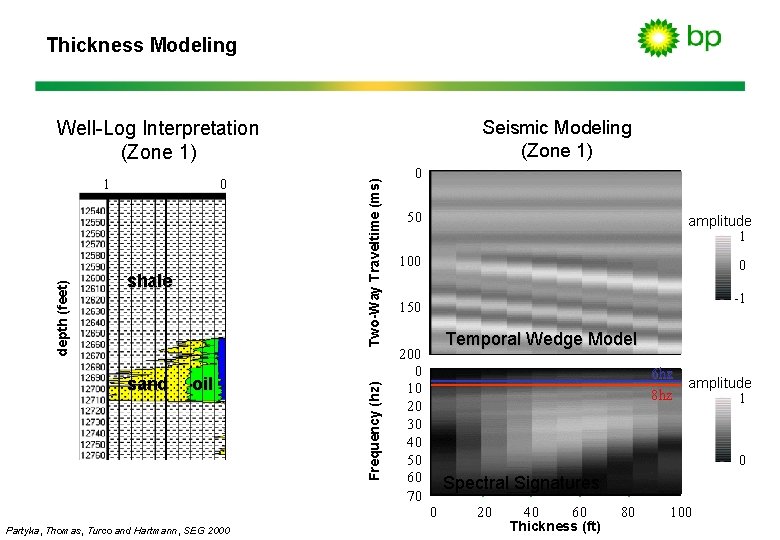
Thickness Modeling Seismic Modeling (Zone 1) 0 shale sand oil Partyka, Thomas, Turco and Hartmann, SEG 2000 Frequency (hz) depth (feet) 1 Two-Way Traveltime (ms) Well-Log Interpretation (Zone 1) 0 50 amplitude 1 100 0 -1 150 200 0 10 20 30 40 50 60 70 Temporal Wedge Model 6 hz amplitude 8 hz 1 0 Spectral Signatures 0 20 40 60 Thickness (ft) 80 100

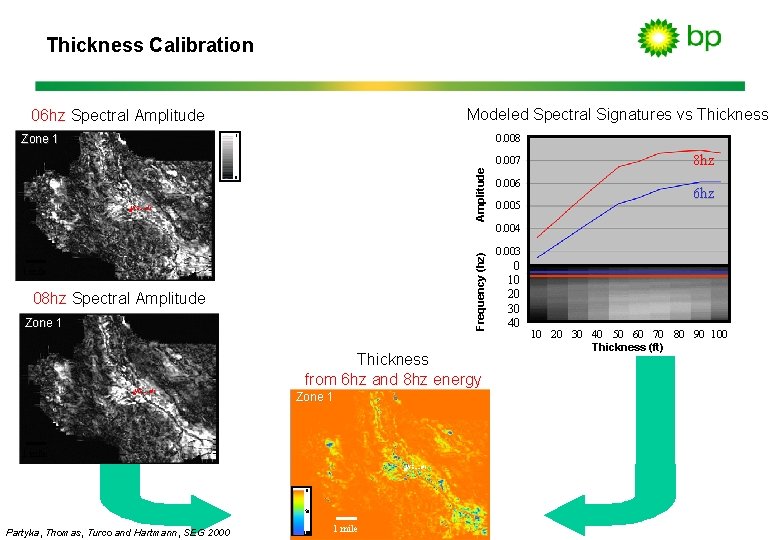
Thickness Calibration Modeled Spectral Signatures vs Thickness 06 hz Spectral Amplitude Zone 1 0. 008 1 Amplitude 0. 007 0 WELL #1 0. 006 0. 005 8 hz amplitude 8 hz 6 hz amplitude 6 hz Frequency (hz) 0. 004 1 mile 08 hz Spectral Amplitude Zone 1 Thickness from 6 hz and 8 hz energy WELL #1 Zone 1 1 mile WELL #1 0 50 Partyka, Thomas, Turco and Hartmann, SEG 2000 1 mile 0. 003 0 10 20 30 40 50 60 70 80 90 100 Thickness (ft)

Outline • Introduction • Three Approaches • Examples • Pros and Cons

Conventional Thickness Estimation • Pros: – user and time intensiveness mandates careful QC. • Cons: – two attributes are required to quantify thickness: • peak-trough time-separation for thickness greater-than the tuning thickness, and • amplitude for thickness less-than the tuning thickness. – user and time intensiveness mandates careful QC.

1 st Dominant Frequency and Amplitude • Pros: – collapses the Tuning Cube into two maps. – does not require careful seismic event picking when the zone of interest is relatively bright. • Cons: – as in the conventional approach, two attributes are required to quantify thickness: • 1 st-dominant frequency for thickness greater-than the tuning thickness, and • 1 st-dominant amplitude for thickness less-than the tuning thickness.

Discrete Frequency Components • Pros: – can be used qualitatively to determine relative thickening/thinning. – can be used quantitatively to calibrate reservoir thickness. – usually exhibit substantially more fidelity than full-bandwidth, conventional amplitude/attributes. Can therefore selectively analyse frequencies exhibitting highest signal fidelity. – usually provide superior rock mass (stratigraphic and structural) and fault definition. – can be integrated with other appropriate information to yield a more comprehensive understanding of the reservoir. – does not require careful seismic event picking when the zone of interest is relatively bright.

Discrete Frequency Components • Cons: – complex layer distributions require seismic modeling analysis to determine relationship between spectral response and thickness.