Segmentation using eigenvectors Papers Normalized Cuts and Image

Segmentation using eigenvectors Papers: “Normalized Cuts and Image Segmentation”. Jianbo Shi and Jitendra Malik, IEEE, 2000 “Segmentation using eigenvectors: a unifying view”. Yair Weiss, ICCV 1999. Presenter: Carlos Vallespi cvalles@cs. cmu. edu

Image Segmentation

Image segmentation l How do you pick the right segmentation? • Bottom up segmentation: - Tokens belong together because they are locally coherent. • Top down segmentation: - Tokens grouped because they lie on the same object.

“Correct” segmentation l There may not be a single correct answer. l Partitioning is inherently hierarchical. l One approach we will use in this presentation: l “Use the low-level coherence of brightness, color, texture or motion attributes to come up with partitions”

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

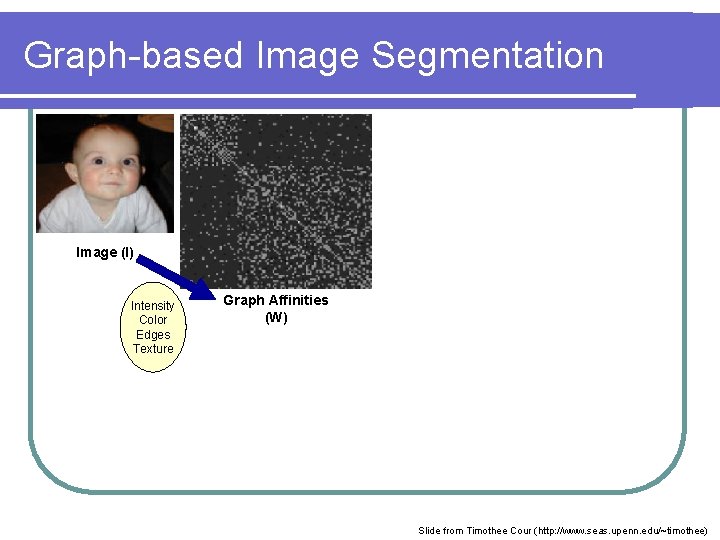
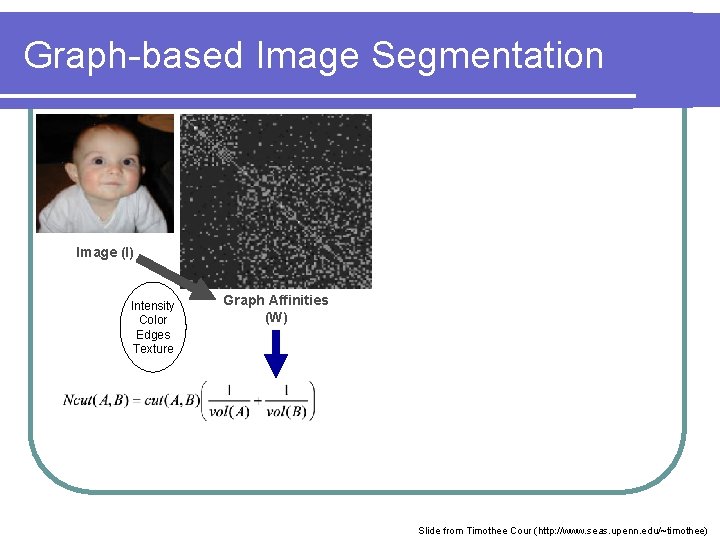
Graph-based Image Segmentation Image (I) Intensity Color Edges Texture Graph Affinities (W) Slide from Timothee Cour (http: //www. seas. upenn. edu/~timothee)

Graph-based Image Segmentation Image (I) Intensity Color Edges Texture Graph Affinities (W) Slide from Timothee Cour (http: //www. seas. upenn. edu/~timothee)

Graph-based Image Segmentation Image (I) Intensity Color Edges Texture Eigenvector X(W) Graph Affinities (W) Slide from Timothee Cour (http: //www. seas. upenn. edu/~timothee)

Graph-based Image Segmentation Image (I) Intensity Color Edges Texture Eigenvector X(W) Discretization Graph Affinities (W) Slide from Timothee Cour (http: //www. seas. upenn. edu/~timothee)

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

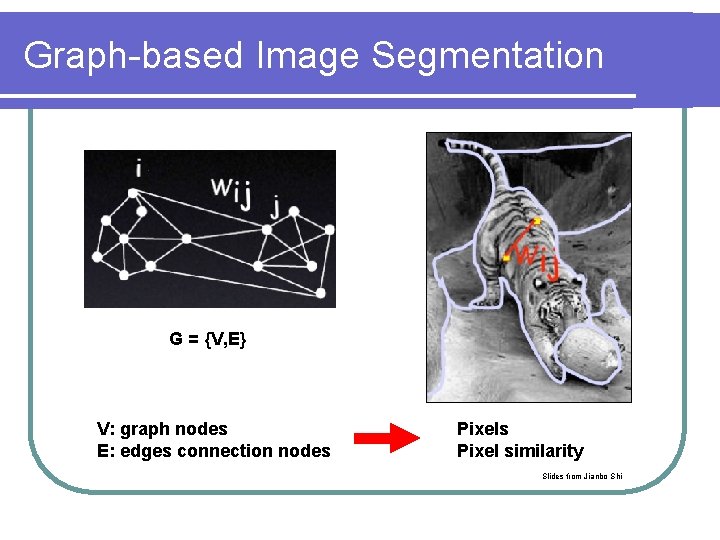
Graph-based Image Segmentation G = {V, E} V: graph nodes E: edges connection nodes Pixel similarity Slides from Jianbo Shi

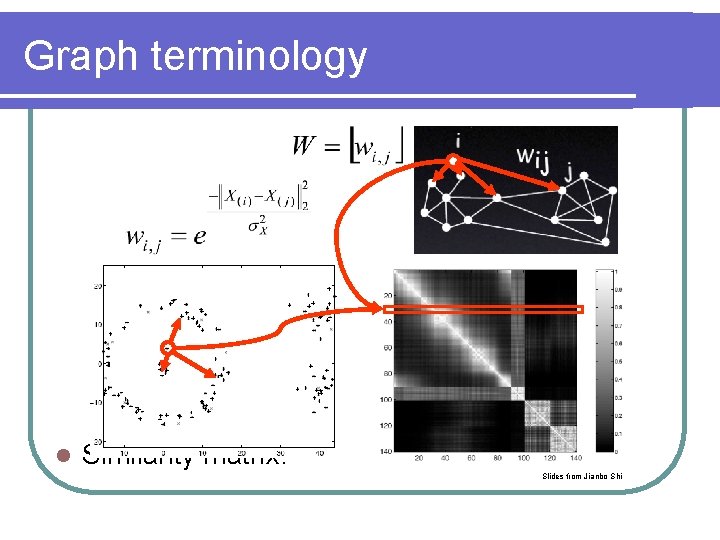
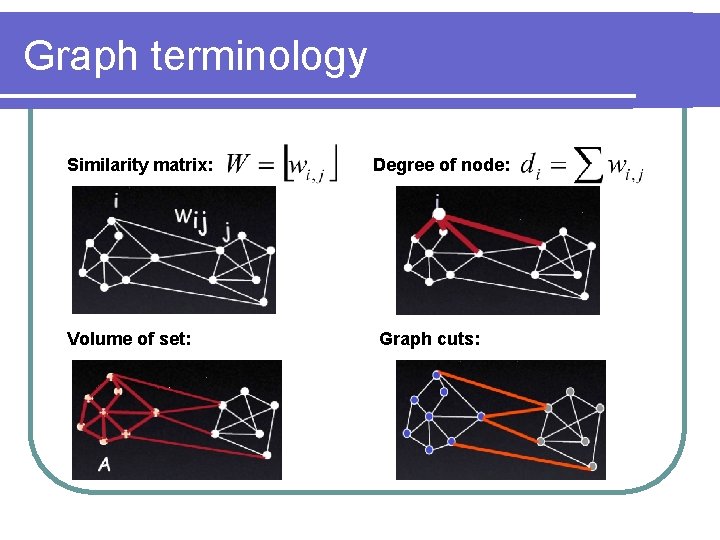
Graph terminology l Similarity matrix: Slides from Jianbo Shi

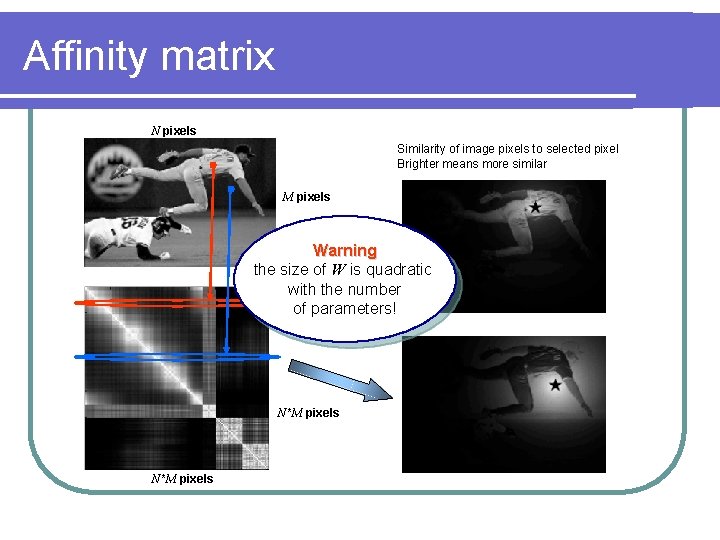
Affinity matrix N pixels Similarity of image pixels to selected pixel Brighter means more similar M pixels Warning the size of W is quadratic with the number of parameters! Reshape N*M pixels

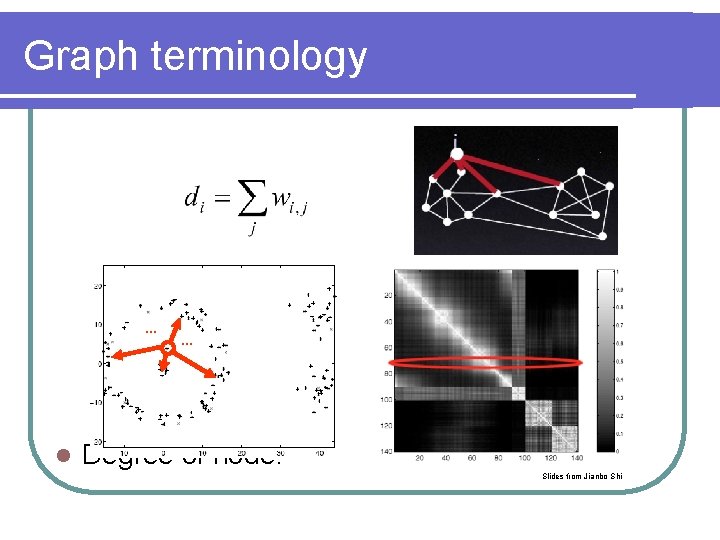
Graph terminology … l … Degree of node: Slides from Jianbo Shi

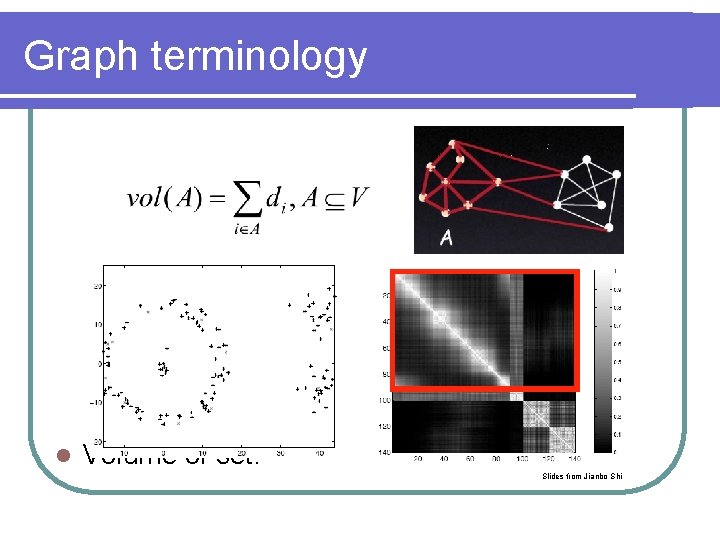
Graph terminology l Volume of set: Slides from Jianbo Shi

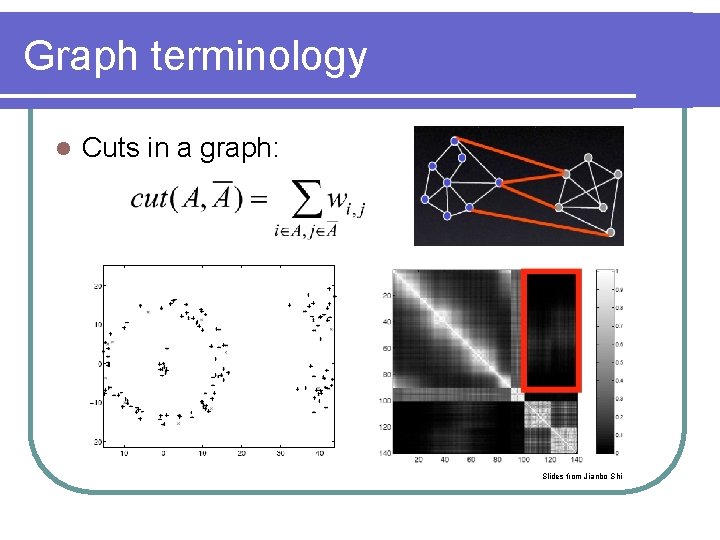
Graph terminology l Cuts in a graph: Slides from Jianbo Shi

Representation Partition matrix X: segments pixels Pair-wise similarity matrix W: Degree matrix D: Laplacian matrix L:

Pixel similarity functions Intensity Distance Texture

Pixel similarity functions Intensity here c(x) is a vector of filter outputs. A natural thing to do is to square the outputs of a range of different filters Distance at different scales and orientations, smooth the result, and rack these into a vector. Texture

Definitions l Methods that use the spectrum of the affinity matrix to cluster are known as spectral clustering l Normalized cuts, Average association make use of the eigenvectors of the affinity matrix. l Why these methods work?

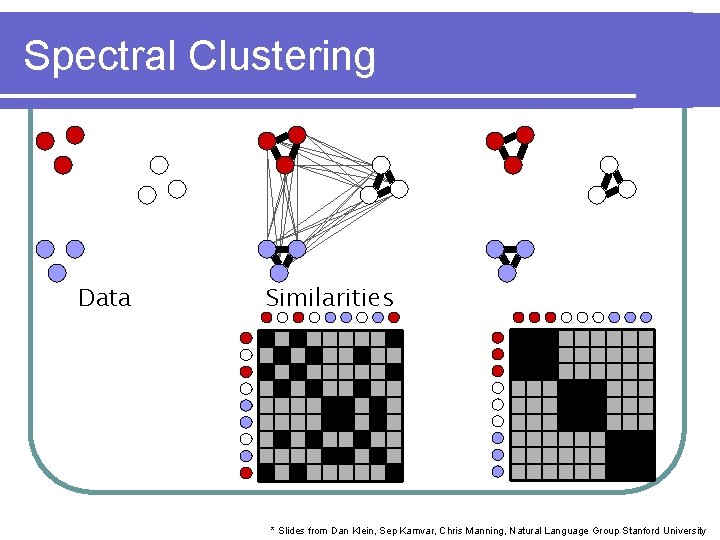
Spectral Clustering Data Similarities * Slides from Dan Klein, Sep Kamvar, Chris Manning, Natural Language Group Stanford University

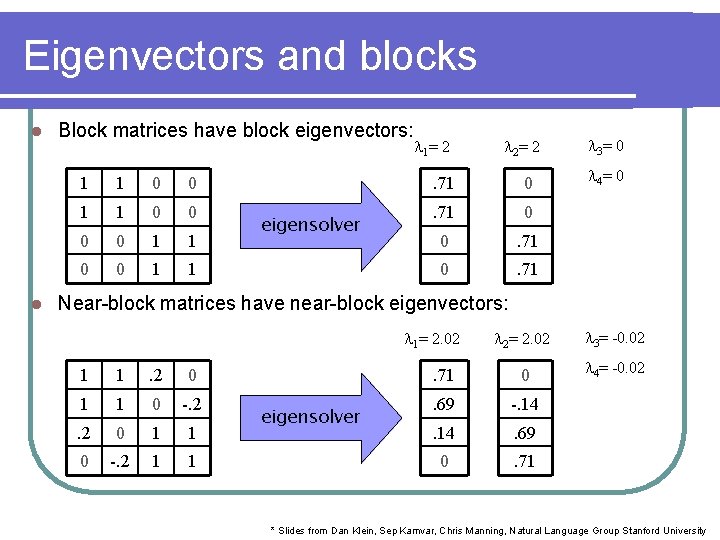
Eigenvectors and blocks l l Block matrices have block eigenvectors: 1 1 0 0 0 0 1 1 eigensolver 1= 2 2= 2 . 71 0 0 . 71 3= 0 4= 0 Near-block matrices have near-block eigenvectors: 2= 2. 02 3= -0. 02 . 71 0 4= -0. 02 . 69 -. 14 . 69 0 . 71 1= 2. 02 1 1 . 2 0 1 1 0 -. 2 1 1 eigensolver * Slides from Dan Klein, Sep Kamvar, Chris Manning, Natural Language Group Stanford University

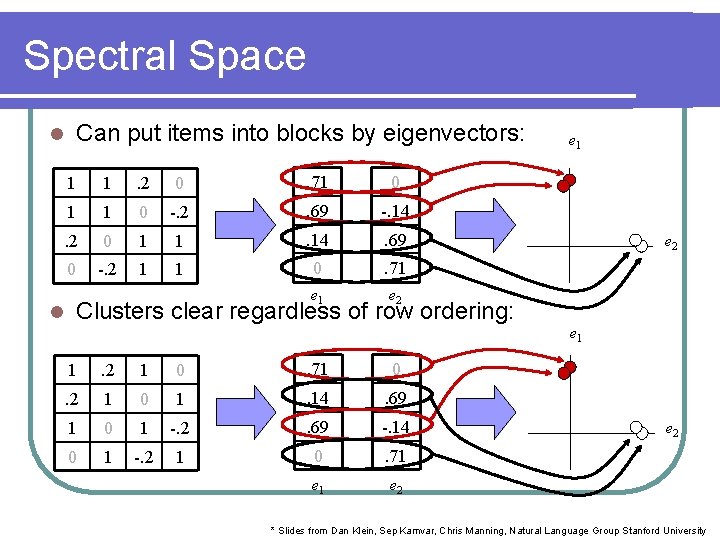
Spectral Space Can put items into blocks by eigenvectors: l l 1 1 . 2 0 . 71 0 1 1 0 -. 2 . 69 -. 14 . 2 0 1 1 . 14 . 69 0 -. 2 1 1 0 . 71 e 2 Clusters clear regardless of row ordering: 1 . 2 1 0 . 71 0 . 2 1 0 1 . 14 . 69 1 0 1 -. 2 . 69 -. 14 0 1 -. 2 1 0 . 71 e 2 e 1 e 2 * Slides from Dan Klein, Sep Kamvar, Chris Manning, Natural Language Group Stanford University

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

How do we extract a good cluster? l l l Simplest idea: idea we want a vector x giving the association between each element and a cluster We want elements within this cluster to, on the whole, have strong affinity with one another We could maximize But need the constraint This is an eigenvalue problem - choose the eigenvector of W with largest eigenvalue.

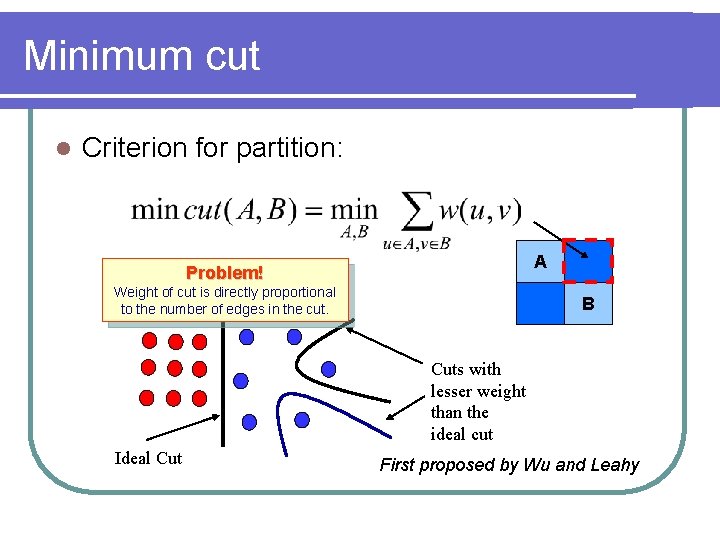
Minimum cut l Criterion for partition: A Problem! Weight of cut is directly proportional to the number of edges in the cut. B Cuts with lesser weight than the ideal cut Ideal Cut First proposed by Wu and Leahy

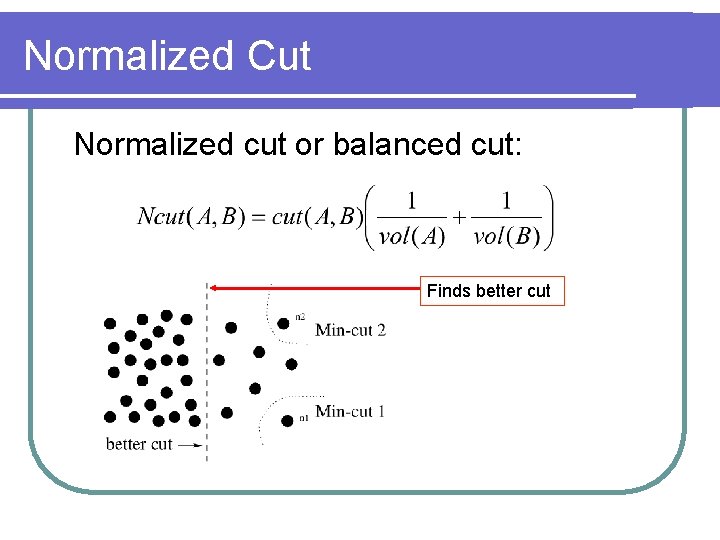
Normalized Cut Normalized cut or balanced cut: Finds better cut

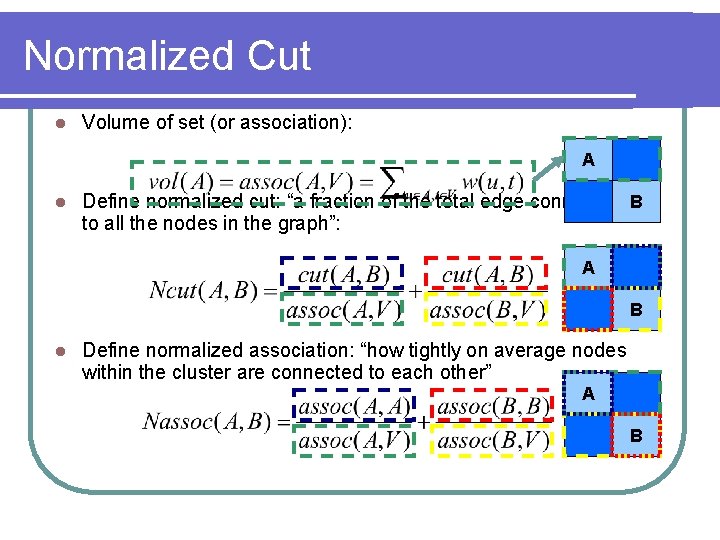
Normalized Cut l Volume of set (or association): A B

Normalized Cut l Volume of set (or association): A l Define normalized cut: “a fraction of the total edge connections. B to all the nodes in the graph”: A B l Define normalized association: “how tightly on average nodes within the cluster are connected to each other” A B

Observations(I) l Maximizing Nassoc is the same as minimizing Ncut, since they are related: l How to minimize Ncut? l l Transform Ncut equation to a matricial form. After simplifying: NP-Hard! y’s values are quantized Subject to: Rayleigh quotient

Observations(II) l Instead, relax into the continuous domain by solving generalized eigenvalue system: min Which gives: l Note that so, the first eigenvector is y 0=1 with eigenvalue 0. l The second smallest eigenvector is the real valued solution to this problem!! l

Algorithm 1. Define a similarity function between 2 nodes. i. e. : 2. Compute affinity matrix (W) and degree matrix (D). Solve Use the eigenvector with the second smallest eigenvalue to bipartition the graph. Decide if re-partition current partitions. 3. 4. 5. Note: since precision requirements are low, W is very sparse and only few eigenvectors are required, the eigenvectors can be extracted very fast using Lanczos algorithm.

Discretization l Sometimes there is not a clear threshold to binarize since eigenvectors take on continuous values. l How to choose the splitting point? a) b) c) Pick a constant value (0, or 0. 5). Pick the median value as splitting point. Look for the splitting point that has the minimum Ncut value: 1. 2. 3. Choose n possible splitting points. Compute Ncut value. Pick minimum.

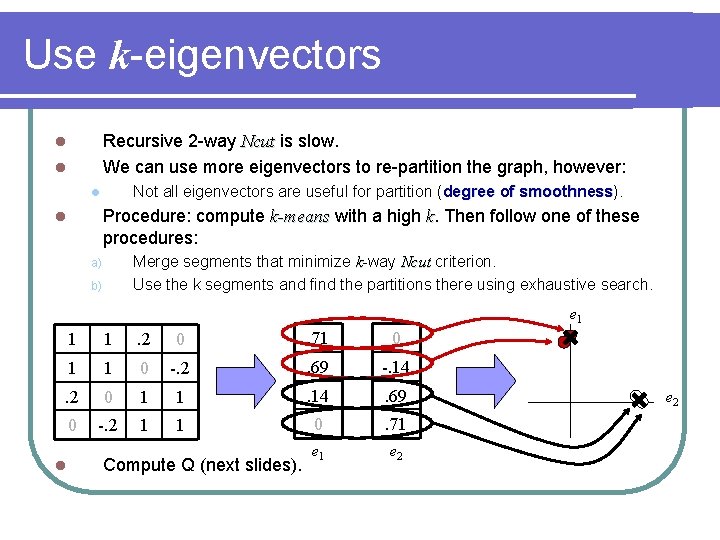
Use k-eigenvectors Recursive 2 -way Ncut is slow. We can use more eigenvectors to re-partition the graph, however: l l Not all eigenvectors are useful for partition (degree of smoothness). smoothness l Procedure: compute k-means with a high k. Then follow one of these procedures: l Merge segments that minimize k-way Ncut criterion. Use the k segments and find the partitions there using exhaustive search. a) b) e 1 1 1 . 2 0 . 71 0 1 1 0 -. 2 . 69 -. 14 . 2 0 1 1 . 14 . 69 0 -. 2 1 1 0 . 71 e 2 l Compute Q (next slides). e 2

Toy examples Images from Matthew Brand (TR-2002 -42)

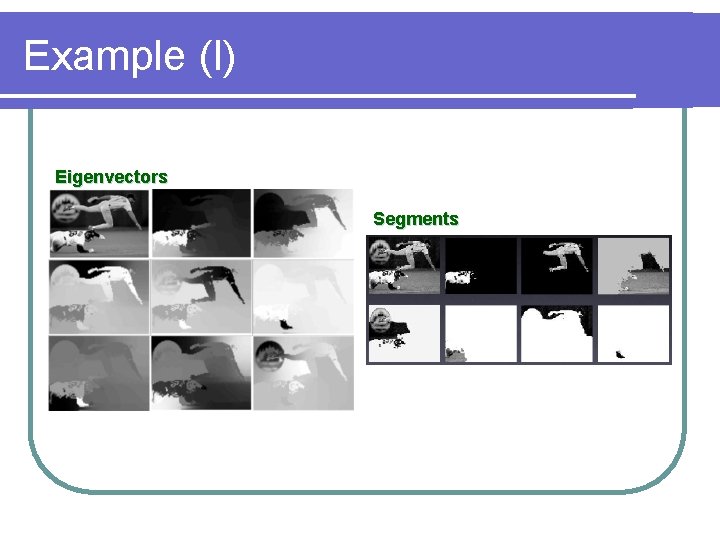
Example (I) Eigenvectors Segments

Example (II) Segments Original * Slide from Khurram Hassan-Shafique CAP 5415 Computer Vision 2003

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

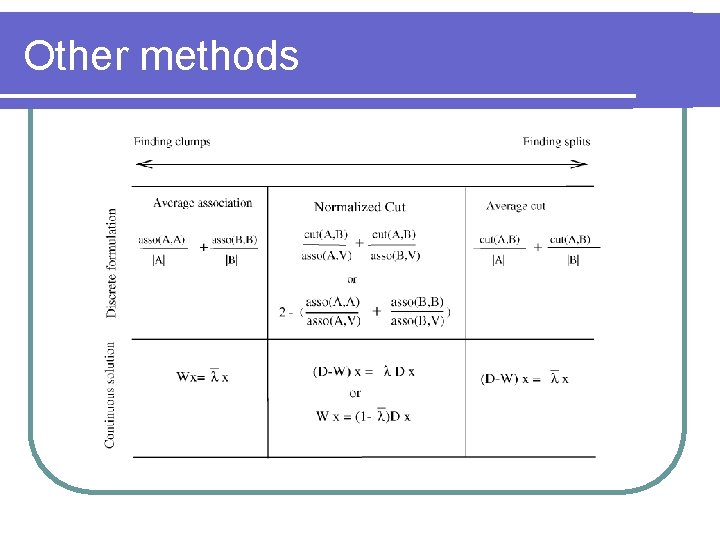
Other methods l Average association Use the eigenvector of W associated to the biggest eigenvalue for partitioning. l Tries to maximize: l A B l Has a bias to find tight clusters. Useful for gaussian distributions.

Other methods l Average l cut Tries to minimize: Very similar to normalized cuts. l We cannot ensure that partitions will have a a tight within-group similarity since this equation does not have the nice properties of the equation of normalized cuts. l

Other methods

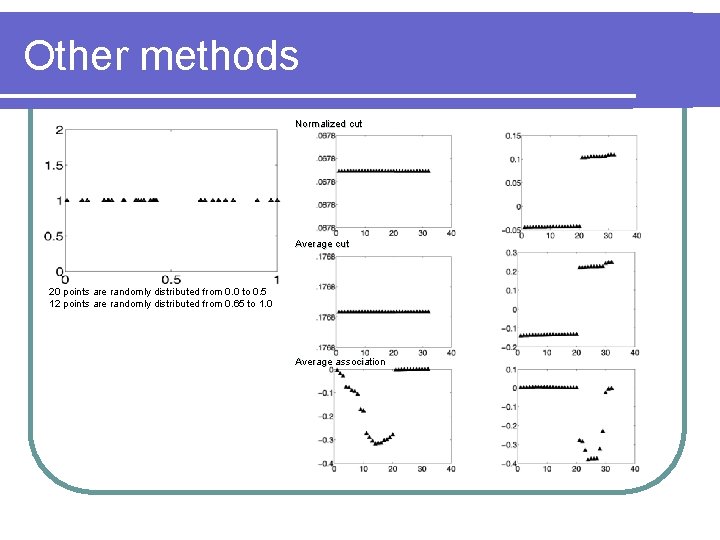
Other methods Normalized cut Average cut 20 points are randomly distributed from 0. 0 to 0. 5 12 points are randomly distributed from 0. 65 to 1. 0 Average association

Other methods Data l W First ev Second ev Q Scott and Longuet-Higgins (1990). l l V contains the first eigenvectors of W. Normalize V by rows. Compute Q=VTV Values close to 1 belong to the same cluster.

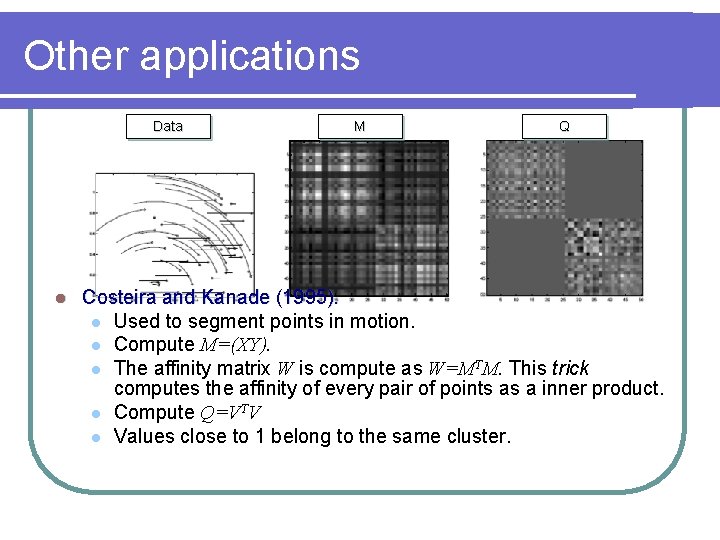
Other applications Data l M Q Costeira and Kanade (1995). l Used to segment points in motion. l Compute M=(XY). l The affinity matrix W is compute as W=MTM. This trick computes the affinity of every pair of points as a inner product. l Compute Q=VTV l Values close to 1 belong to the same cluster.

Other applications l Face clustering in meetings. l l l Grab faces from video in real time (use a face detector + face tracker). Compare all faces using a distance metric (i. e. projection error into representative basis). Use normalized cuts to find best clustering.

Outline 1. 2. 3. 4. 5. Introduction Graph terminology and representation. “Min cuts” and “Normalized cuts”. Other segmentation methods using eigenvectors. Conclusions.

Conclusions l Good news: l l l Simple and powerful methods to segment images. Flexible and easy to apply to other clustering problems. Bad news: l l High memory requirements (use sparse matrices). Very dependant on the scale factor for a specific problem.

The End! Thank you!

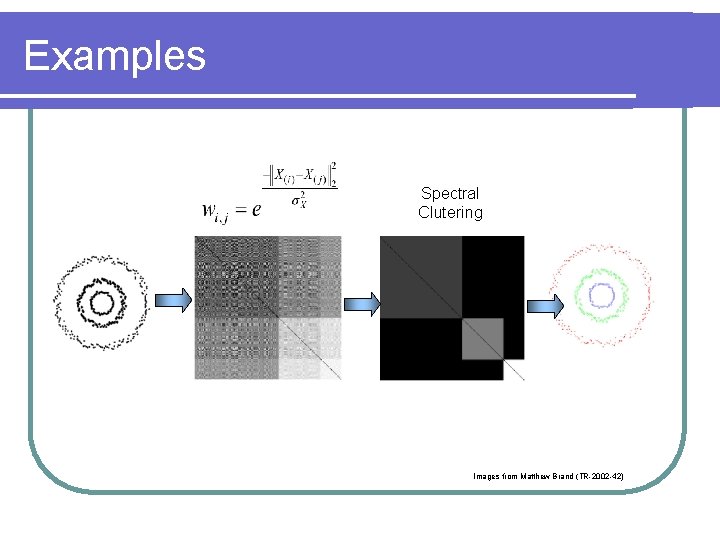
Examples Spectral Clutering Images from Matthew Brand (TR-2002 -42)

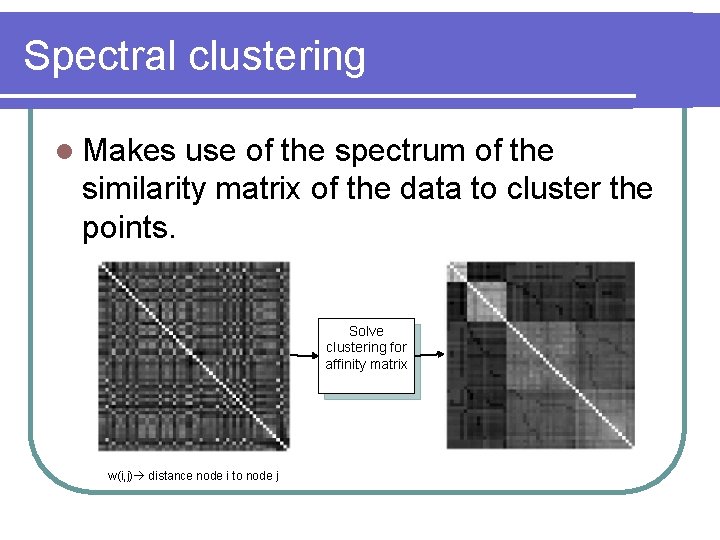
Spectral clustering l Makes use of the spectrum of the similarity matrix of the data to cluster the points. Solve clustering for affinity matrix w(i, j) distance node i to node j

Graph terminology Similarity matrix: Volume of set: Degree of node: Graph cuts: