Segmentasi Citra Thresholding Basic Global Thresholding 1 2

Segmentasi Citra

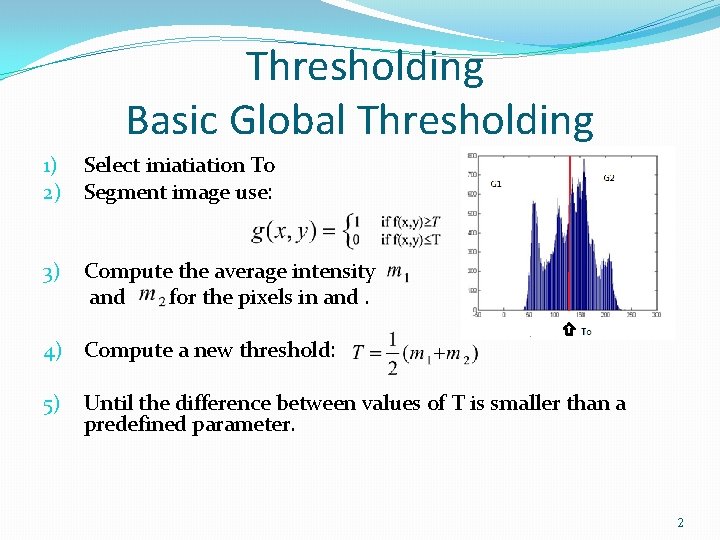
Thresholding Basic Global Thresholding 1) 2) Select iniatiation To Segment image use: 3) Compute the average intensity and for the pixels in and. 4) Compute a new threshold: 5) Until the difference between values of T is smaller than a predefined parameter. 2

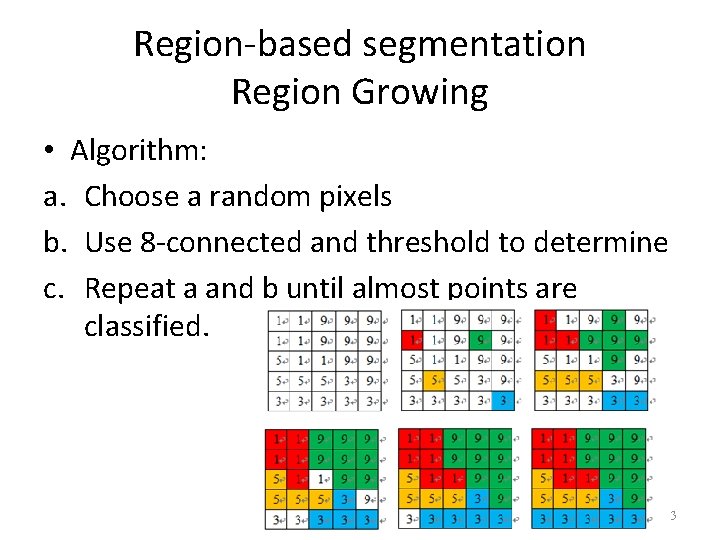
Region-based segmentation Region Growing • Algorithm: a. Choose a random pixels b. Use 8 -connected and threshold to determine c. Repeat a and b until almost points are classified. 3

Image segmentation using k-mean clustering • There are K clusters C 1, …, CK with means m 1, …, m. K. • The least-squares error is defined as K D= 2 || xi - mk ||. k=1 xi Ck • Out of all possible partitions into K clusters, choose the one that minimizes D. Why don’t we just do this? If we could, would we get meaningful objects?

K-Means Clustering Form K-means clusters from a set of n-dimensional vectors 1. Set ic (iteration count) to 1 2. Choose randomly a set of K means m 1(1), …, m. K(1). 3. For each vector xi compute D(xi , mk(ic)), k=1, …K and assign xi to the cluster Cj with nearest mean. 4. Increment ic by 1, update the means to get m 1(ic), …, m. K(ic). 5. Repeat steps 3 and 4 until Ck(ic) = Ck(ic+1) for all k.

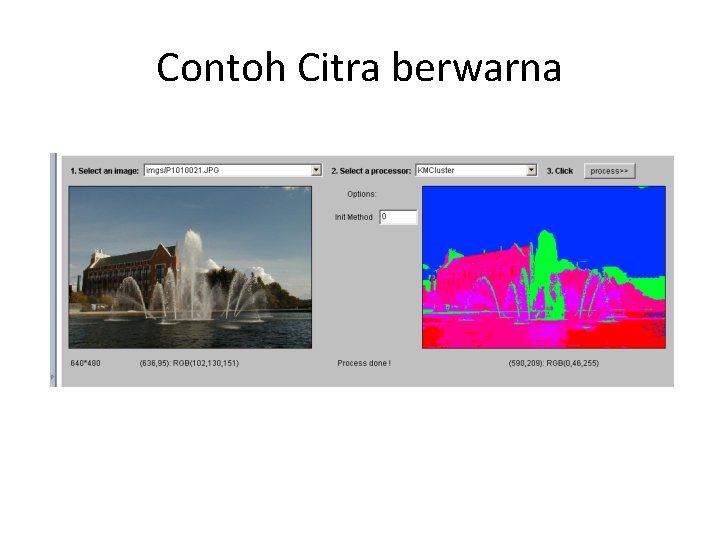
Contoh Citra berwarna

Clustering in Color Space 1. Each image point is mapped to a point in a color space, e. g. : Color(i, j) = (R (i, j), G(i, j), B(i, j)) It is many to one mapping. 2. The points in the color space are grouped to clusters. 3. The clusters are then mapped back to regions in the image.

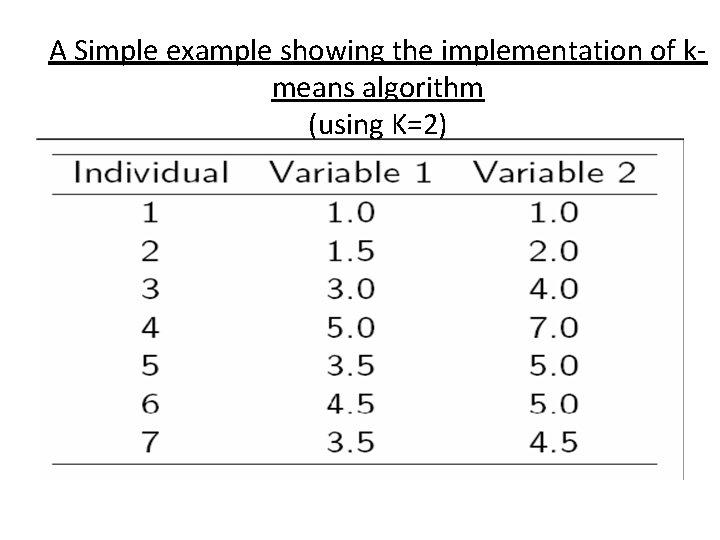
A Simple example showing the implementation of kmeans algorithm (using K=2)

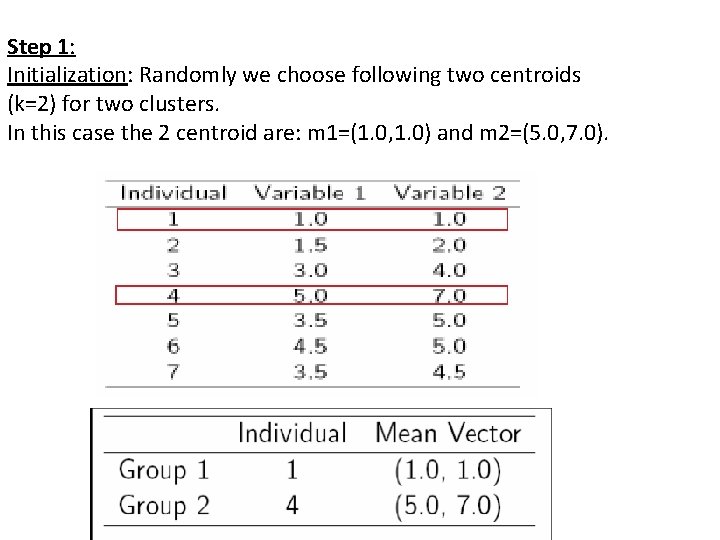
Step 1: Initialization: Randomly we choose following two centroids (k=2) for two clusters. In this case the 2 centroid are: m 1=(1. 0, 1. 0) and m 2=(5. 0, 7. 0).

Step 2: • Thus, we obtain two clusters containing: {1, 2, 3} and {4, 5, 6, 7}. • Their new centroids are:

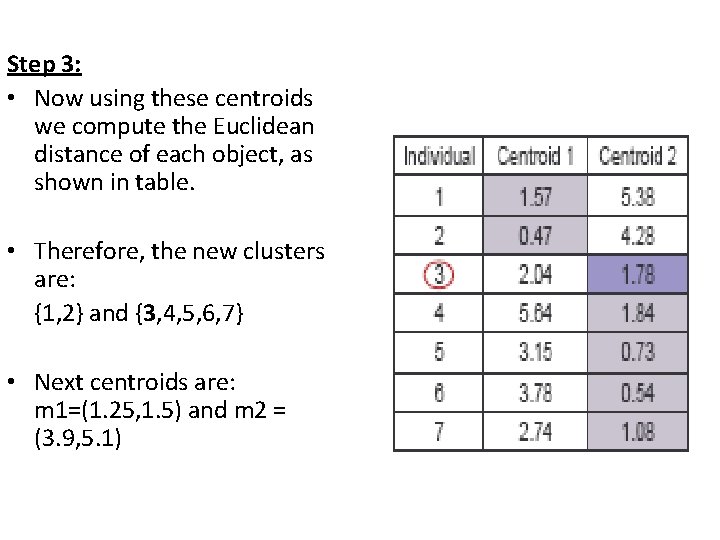
Step 3: • Now using these centroids we compute the Euclidean distance of each object, as shown in table. • Therefore, the new clusters are: {1, 2} and {3, 4, 5, 6, 7} • Next centroids are: m 1=(1. 25, 1. 5) and m 2 = (3. 9, 5. 1)

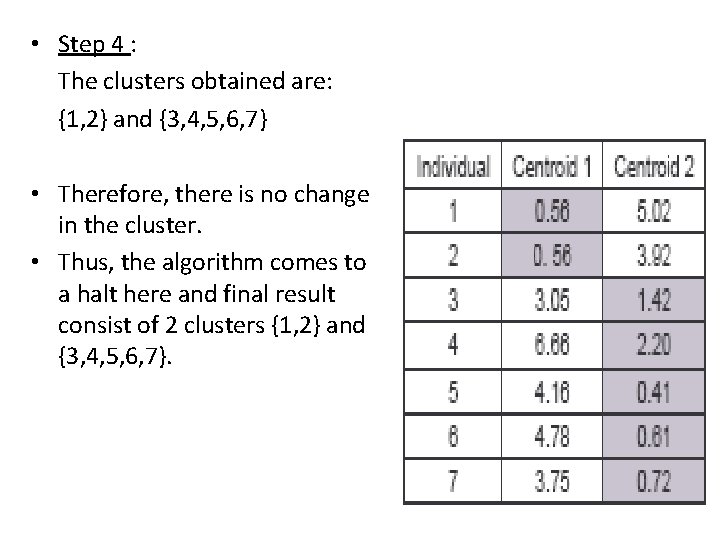
• Step 4 : The clusters obtained are: {1, 2} and {3, 4, 5, 6, 7} • Therefore, there is no change in the cluster. • Thus, the algorithm comes to a halt here and final result consist of 2 clusters {1, 2} and {3, 4, 5, 6, 7}.

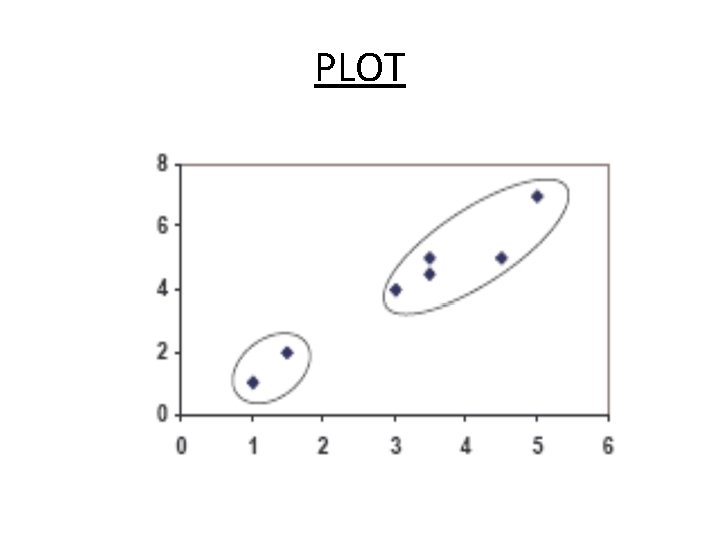
PLOT