Segment Tree and Its VLSI Layout Applications Shmuel

Segment Tree and Its VLSI Layout Applications Shmuel Wimer Bar Ilan Univ. , School of Engineering Jan 2011 Segment Tree 1

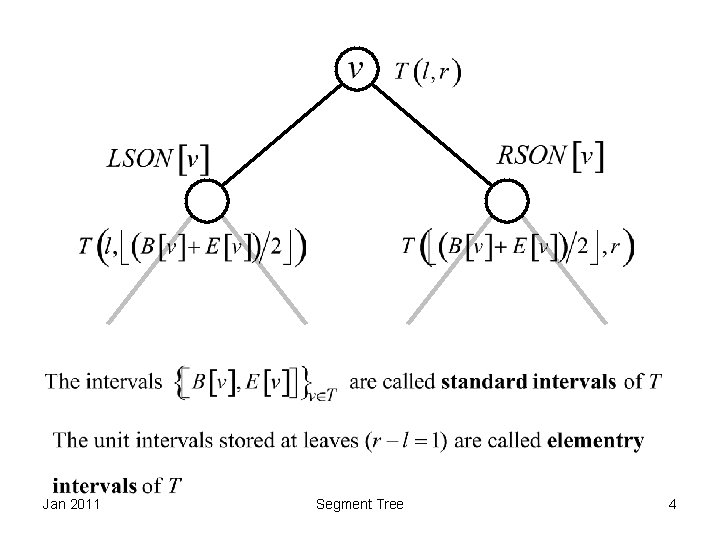
Segment Tree Definition • Introduced by J. L. Bentley in 1977 • Data structure designed to handle intervals on the real line • Intervals end points belong to a fixed set of abscissas • Abscissas can be normalized to range [1, N] without loss of generality by using a lookup table • Given an interval [l, r], the segment tree T(l, r) is a rooted binary tree defined recursively Jan 2011 Segment Tree 2

Jan 2011 Segment Tree 3

Jan 2011 Segment Tree 4

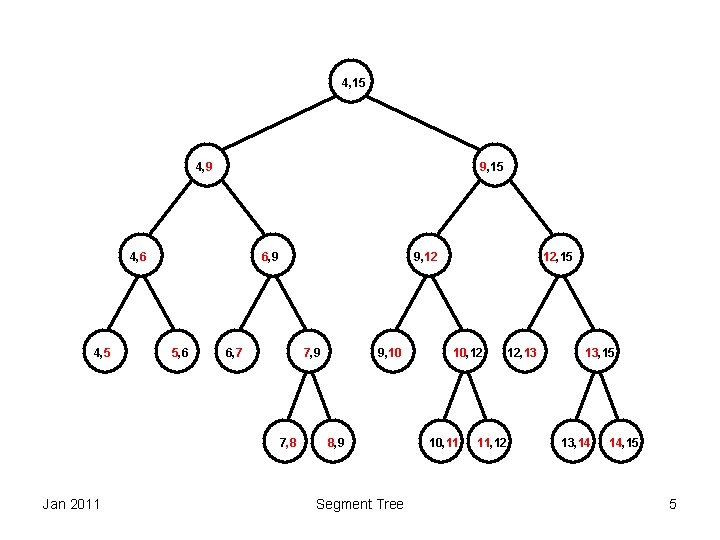
4, 15 4, 9 9, 15 4, 6 4, 5 6, 9 5, 6 9, 12 6, 7 7, 9 7, 8 Jan 2011 9, 10 8, 9 Segment Tree 12, 15 10, 12 10, 11 11, 12 12, 13 13, 15 13, 14 14, 15 5

Insertion and Deletion Jan 2011 Segment Tree 6

Jan 2011 Segment Tree 7

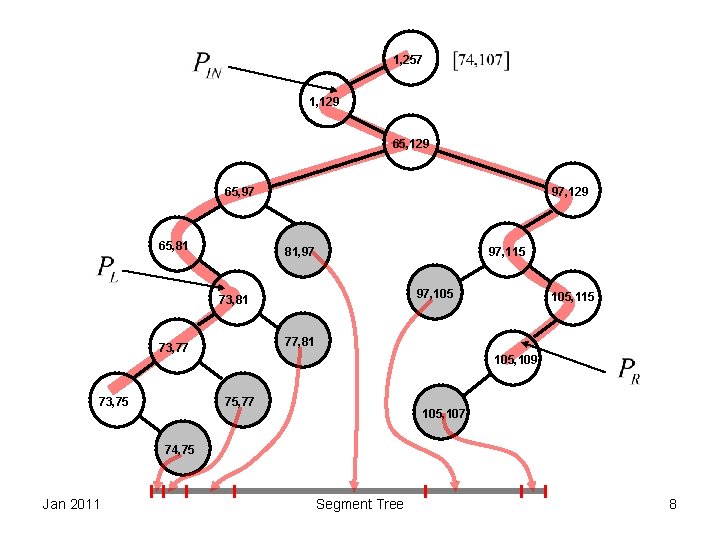
1, 257 1, 129 65, 97 65, 81 97, 129 97, 115 81, 97 97, 105 73, 81 77, 81 73, 77 73, 75 105, 115 105, 109 75, 77 105, 107 74, 75 Jan 2011 Segment Tree 8

Jan 2011 Segment Tree 9

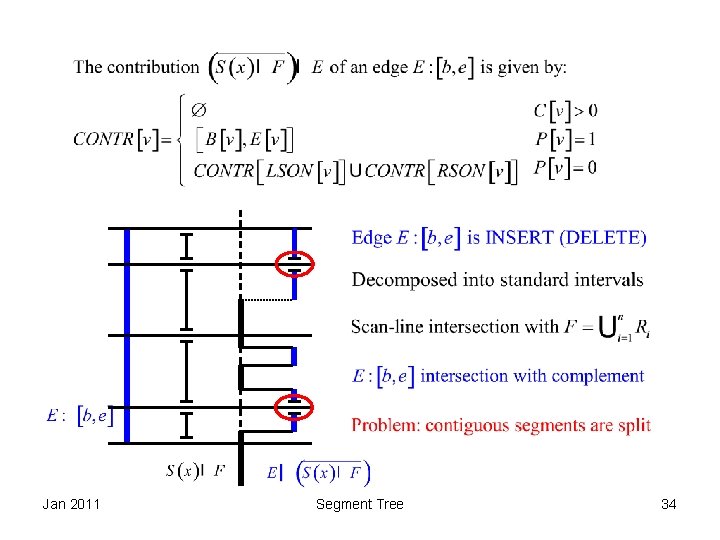
Allocation and De-Allocation • Depends on application. • If we wish to know the cardinality of cover of [B[v], E[v]] then a counter C[v] is associated with node v: – C[v] = C[V]+1 is allocation for INSERT – C[v] = C[V]-1 is de-allocation for DELETE • In many cases of VLSI aplication C[v] indicates the presence of material, so we’ll be interested in whether C[v] > 0 (material exists) or C[v]==0 (no material). Jan 2011 Segment Tree 10

VLSI Layout Applications • Useful for calculating area and perimeter of polygon ensemble for lateral and fringe capacitance extraction. • Mask Boolean operations like UNION, INTERSECTION, DIFFERENCE, and more, where contour is required. – Construction (contour) problems are typically more difficult than reporting (area, perimeter) problems. • More applications: – Design rule checking. – Cross coupling capacitance • Very robust and simple for implementation. There are other, more efficient and more complex data structures. Jan 2011 Segment Tree 11

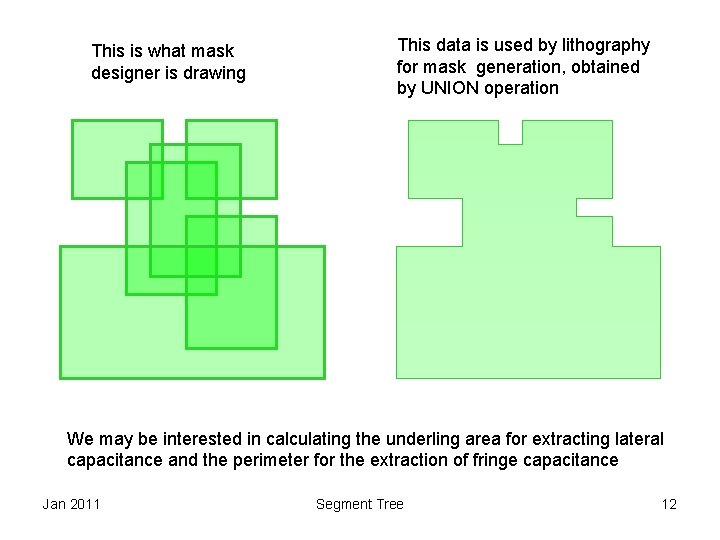
This is what mask designer is drawing This data is used by lithography for mask generation, obtained by UNION operation We may be interested in calculating the underling area for extracting lateral capacitance and the perimeter for the extraction of fringe capacitance Jan 2011 Segment Tree 12

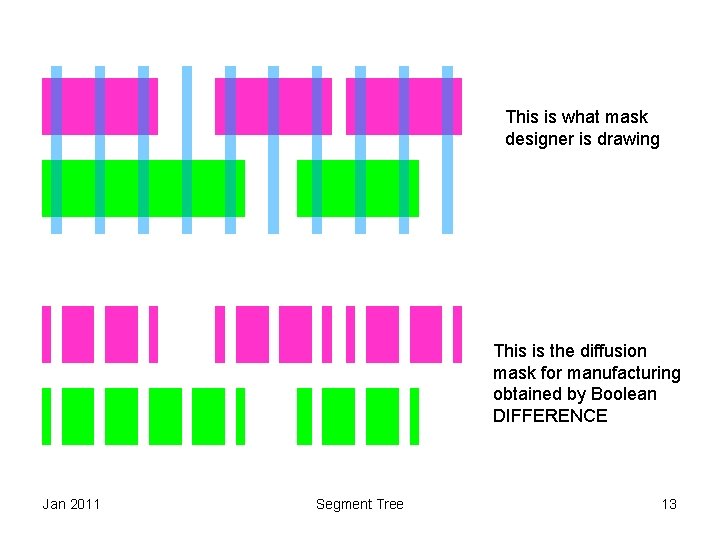
This is what mask designer is drawing This is the diffusion mask for manufacturing obtained by Boolean DIFFERENCE Jan 2011 Segment Tree 13

The electric field between the metal wires implies line-to-line capacitance, which is the reason of noise and power dissipation This is what mask designer is drawing L D We’d like to calculate the common parallel run L and the distance D so the line-to-line capacitance is L/D Jan 2011 Segment Tree 14

1 D Measure of Union of Intervals Jan 2011 Segment Tree 15

Jan 2011 Segment Tree 16

2 D Measure (Area) of Union of Rectangles Jan 2011 Segment Tree 17

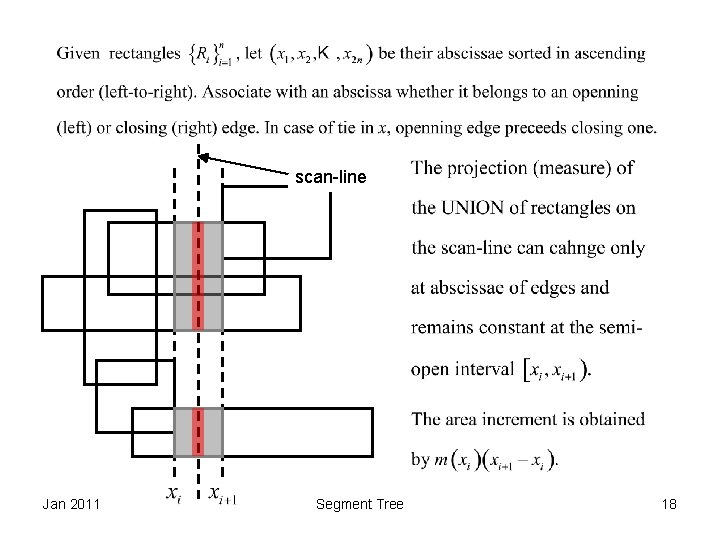
scan-line Jan 2011 Segment Tree 18

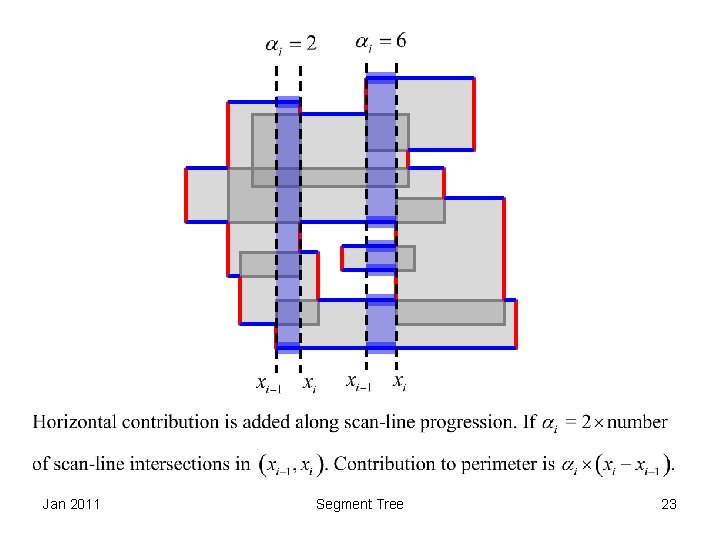
Efficient Calculation of m(xi) Jan 2011 Segment Tree 19

Jan 2011 Segment Tree 20

Jan 2011 Segment Tree 21

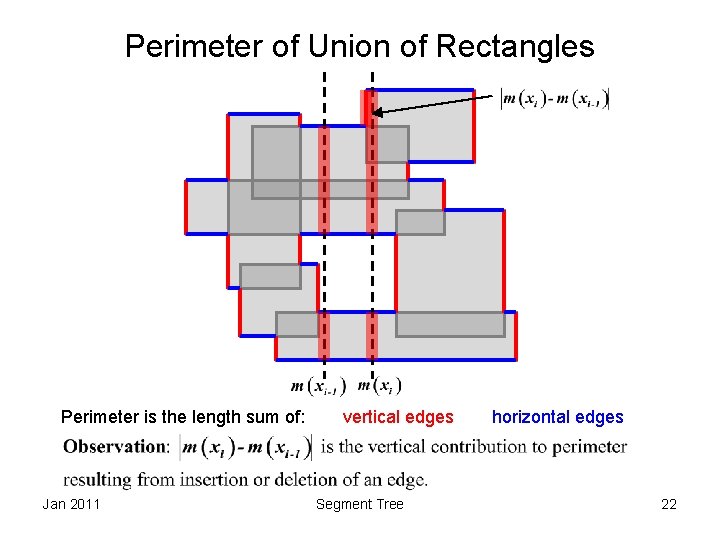
Perimeter of Union of Rectangles Perimeter is the length sum of: Jan 2011 vertical edges Segment Tree horizontal edges 22

Jan 2011 Segment Tree 23

Jan 2011 Segment Tree 24

Jan 2011 Segment Tree 25

Jan 2011 Segment Tree 26

Jan 2011 Segment Tree 27

Jan 2011 Segment Tree 28

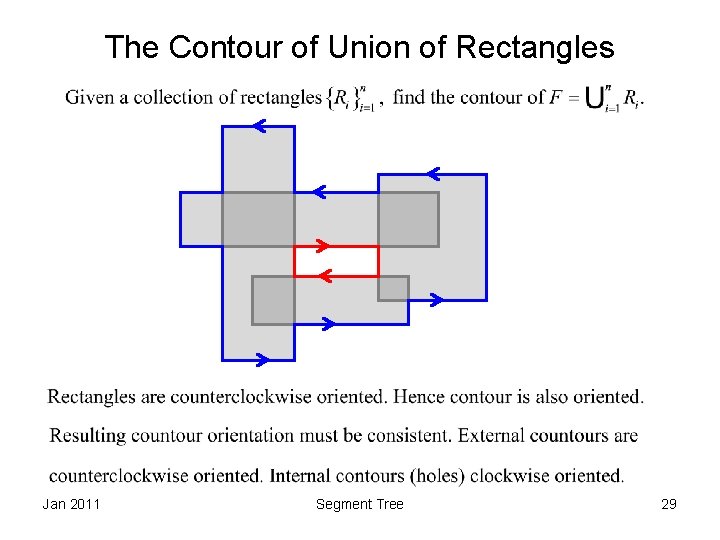
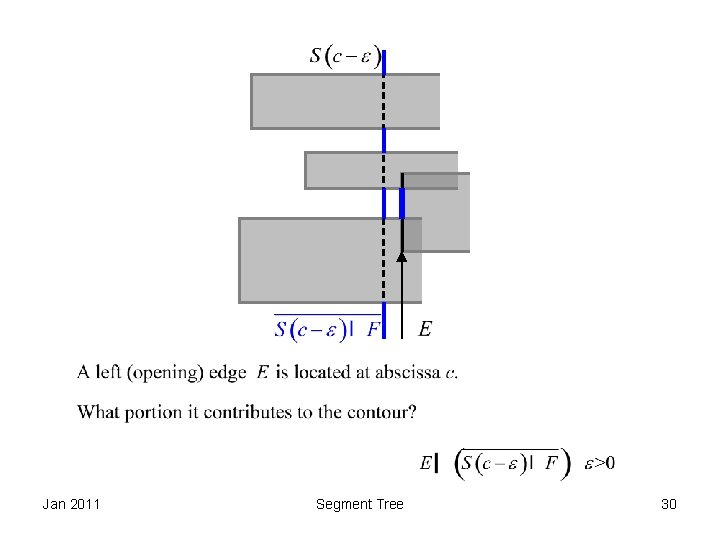
The Contour of Union of Rectangles Jan 2011 Segment Tree 29

Jan 2011 Segment Tree 30

Jan 2011 Segment Tree 31

Jan 2011 Segment Tree 32

Jan 2011 Segment Tree 33

Jan 2011 Segment Tree 34

Jan 2011 Segment Tree 35

Jan 2011 Segment Tree 36

Jan 2011 Segment Tree 37

Jan 2011 Segment Tree 38

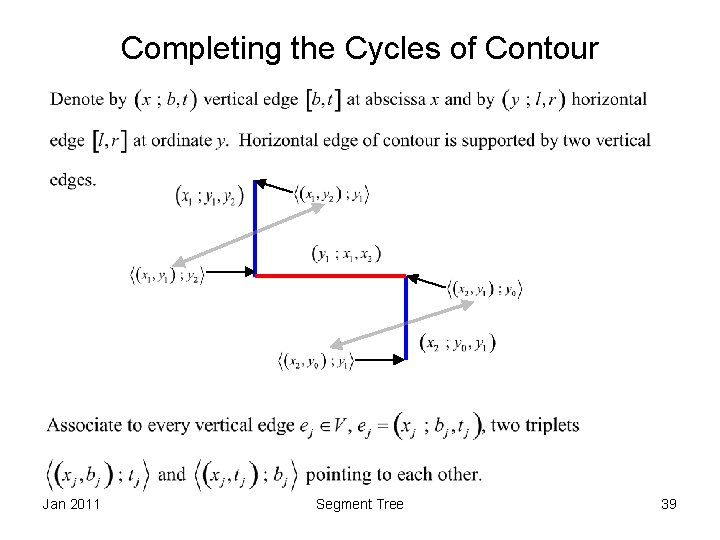
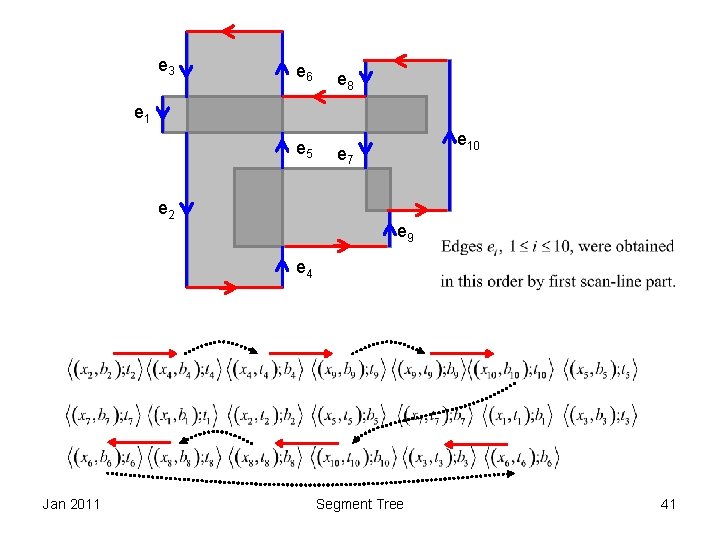
Completing the Cycles of Contour Jan 2011 Segment Tree 39

Jan 2011 Segment Tree 40

e 3 e 6 e 8 e 5 e 7 e 1 e 2 e 10 e 9 e 4 Jan 2011 Segment Tree 41

There’s no ambiguity in deciding whether to go to left or right triplet when an horizontal edge is decided. It follows that a pair of successive triplets defines horizontal edges. Consequently, once two successive triplets are traversed and define a new horizontal edge, the number of triplets on both the left and the right parts of the list must be even. Therefore, if the index of a triplet is even, its left adjacent triplet is paired, otherwise, the right triplet is paired. Jan 2011 Segment Tree 42

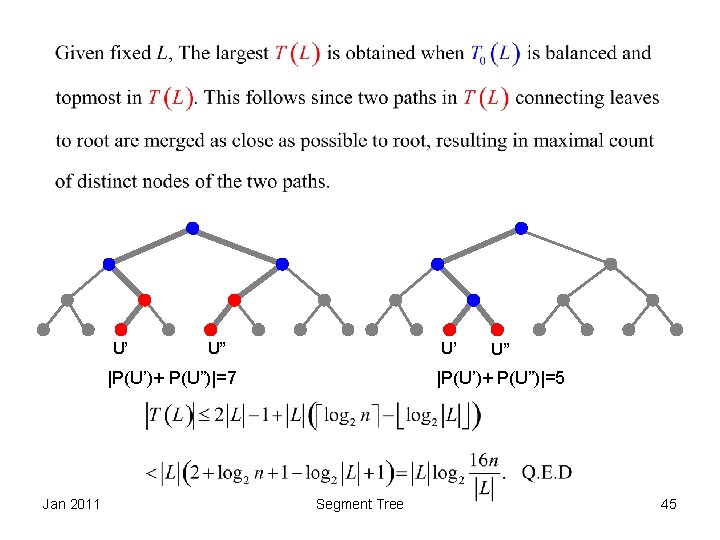
Run-time Complexity Jan 2011 Segment Tree 43

Jan 2011 Segment Tree 44

U’ U” U’ |P(U’)+ P(U”)|=7 Jan 2011 U” |P(U’)+ P(U”)|=5 Segment Tree 45

Jan 2011 Segment Tree 46

Jan 2011 Segment Tree 47

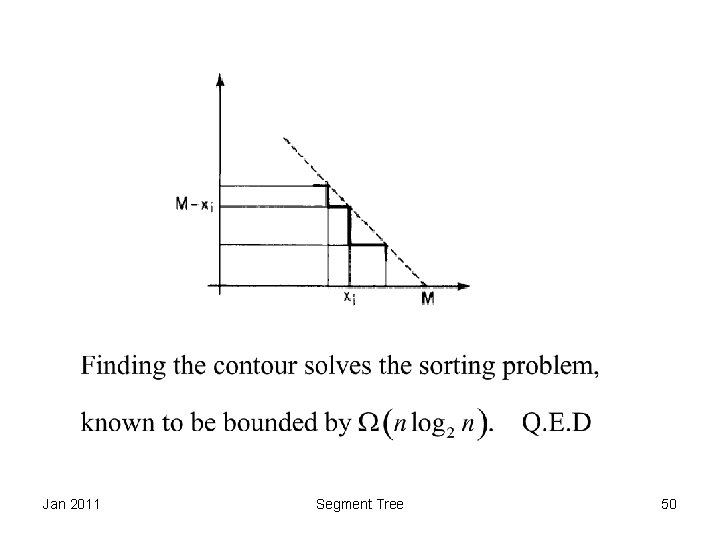
Jan 2011 Segment Tree 48

Jan 2011 Segment Tree 49

Jan 2011 Segment Tree 50