Segment Intersection Chapter 2 SegmentSegment Intersection Computing the



















- Slides: 29

Segment Intersection Chapter 2

Segment-Segment Intersection • Computing the point of intersection – We know that they intersect (assume) • = t 1 a 1 + (1 -t 1) a 2 • = t 1 b 1 + (1 -t 1) b 2 (1) (2) (c 1, d 1) (a 2, b 2) ( , ) • = t 2 c 1 + (1 -t 2) c 2 • = t 2 d 2 + (1 -t 2) d 2 • From (1) and (3) we get: • From (2) and (4) we get: (3) (4) (a 1, b 1) (c 2, d 2) (a 1 -a 2)t 1 + a 2 = (c 1 -c 2) t 2 + c 2 (5) (b 1 -b 2)t 1 + b 2 = (d 1 -d 2) t 2 + d 2 (6)

Segment-Segment Intersection • Solving (5) and (6) gives: • [(d 1 -d 2)(a 1 -a 2) – (c 1 -c 2)(b 1 -b 2)]t 1 = (c 1 -c 2) (b 2 -d 2) – (d 1 -d 2)(a 2 -c 2) • [(b 1 -b 2)(c 1 -c 2) – (a 1 -a 2)(d 1 -d 2)]t 2 = (a 1 -a 2)(d 2 -b 2) – (b 1 -b 2)(c 2 -a 2) • Thus t 1 and t 2 can be computed • It is possible that some of the divisors could be small

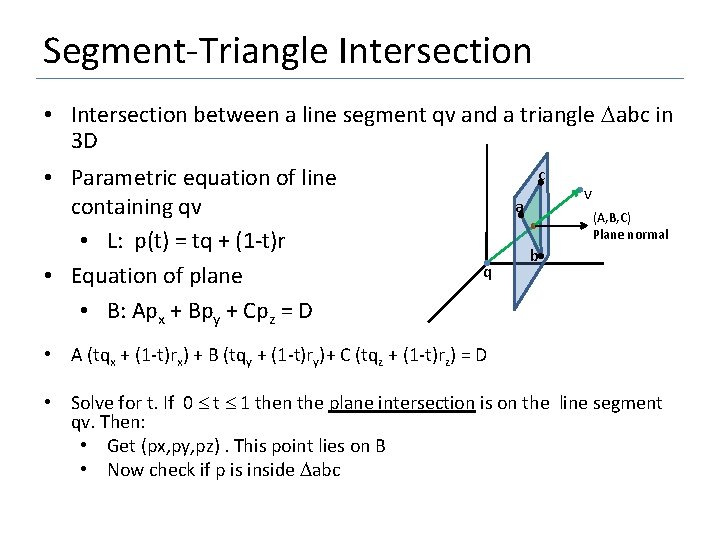
Segment-Triangle Intersection • Intersection between a line segment qv and a triangle abc in 3 D • Parametric equation of line containing qv • L: p(t) = tq + (1 -t)r • Equation of plane • B: Apx + Bpy + Cpz = D c a q v (A, B, C) Plane normal b • A (tqx + (1 -t)rx) + B (tqy + (1 -t)ry)+ C (tqz + (1 -t)rz) = D • Solve for t. If 0 t 1 then the plane intersection is on the line segment qv. Then: • Get (px, py, pz). This point lies on B • Now check if p is inside abc

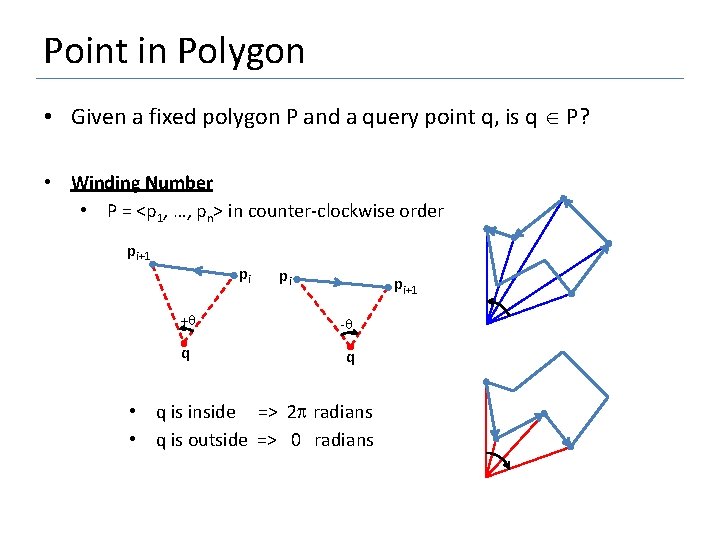
Point in Polygon • Given a fixed polygon P and a query point q, is q P? • Winding Number • P = <p 1, …, pn> in counter-clockwise order pi+1 pi + q pi pi+1 - q • q is inside => 2 radians • q is outside => 0 radians

Point in Polygon • Ray Crossing • Draw a ray rq from q • Determine the number of intersections of P with rq • Odd number => inside • Even number => outside q q count twice count once q rq rq q count once rq rq

Point Location in 3 -D • Generate a random ray rq from q • If rq is degenerate, generate another ray • Inside-outside test is the same as in 2 D

Segment Intersection • Problem: • Given: A set of n distinct segments s 1, s 2, …, sn represented by coordinates endpoints • Goal (A): • Detect if there is any si sj that intersect • Goal (B): • Report all pairs of intersecting segments

Segment Intersection • Applications: • Circuit design • Clipping, windowing • Map overlay • Some Approaches: • Easy to solve in O(n 2) time (brute force). Needs extra effort if the arrangement is required. • We will see that • Can do better for the detection problem • The number of intersections k is usually small. We would like an output sensitive algorithm whose running time is fast if k is small

Segment Intersection • Bucketing • Divide up the plane using a uniform grid • Distribute segments to the squares in the grid • Find intersections within each grid square • Can be quite fast for evenly distributed data

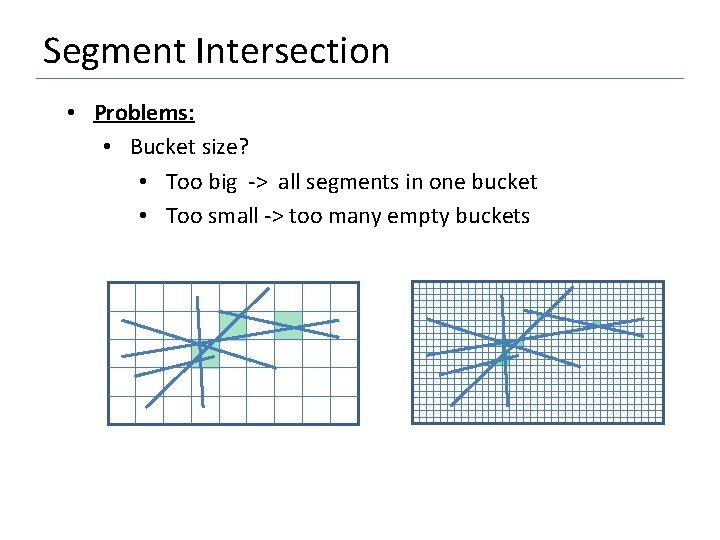
Segment Intersection • Problems: • Bucket size? • Too big -> all segments in one bucket • Too small -> too many empty buckets

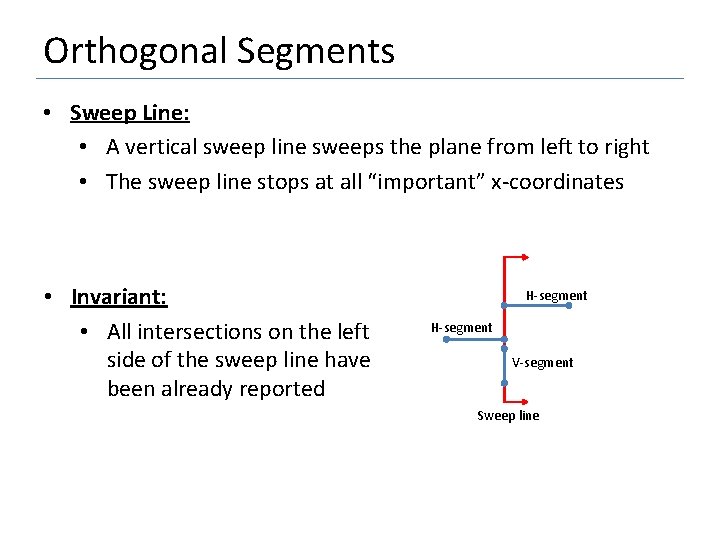
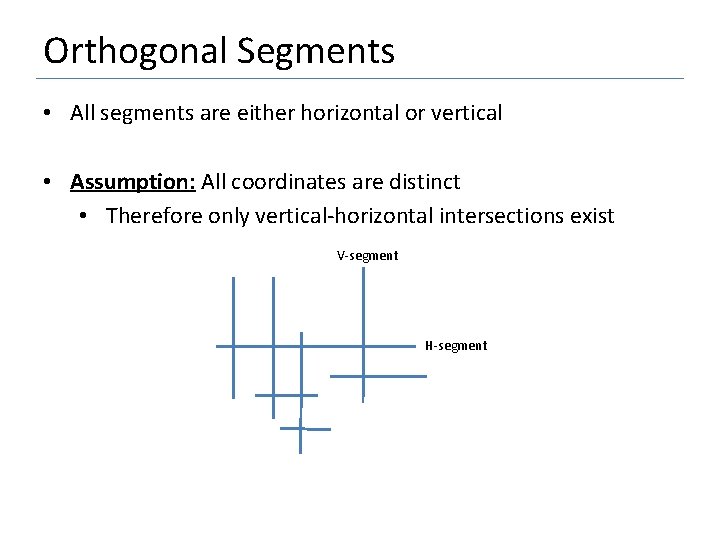
Orthogonal Segments • Sweep Line: • A vertical sweep line sweeps the plane from left to right • The sweep line stops at all “important” x-coordinates • Invariant: • All intersections on the left side of the sweep line have been already reported H-segment V-segment Sweep line

Orthogonal Segments • All segments are either horizontal or vertical • Assumption: All coordinates are distinct • Therefore only vertical-horizontal intersections exist V-segment H-segment

Arbitrary Line Segments • Result: We will show: • O(nlogn) time for the detection problem • O(nlogn + klogn) time for the reporting problem • Using Line-sweep approach • Optimal • Balaban’s algorithm that solves the reporting problem in O(nlogn+k) time.

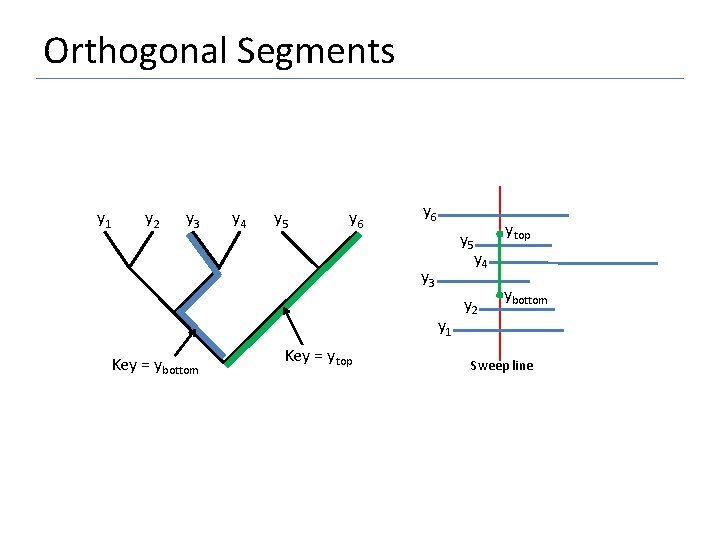
Orthogonal Segments • We maintain sorted y-coordinates of H-segments currently intersected by the sweep line (using a balanced binary search tree T) • When we hit the left endpoint of an H-segment, we add it’s ycoordinate to T. • When the sweep line hits the right endpoint of an H-segment, we delete its y-coordinate form T • Whenever the sweep line hits a V-segment with coordinates (ybottom, ytop), we report all H-segments in T with y-coordinates in the range [ybottom, ytop]

Orthogonal Segments y 1 y 2 y 3 y 4 y 5 y 6 y 5 y 4 y 3 y 1 Key = ybottom Key = ytop y 2 ytop ybottom Sweep line

Orthogonal Segments • Algorithm: • Sort all V-segments and endpoints of H-segments by their x-coordinates • These points give the event points of the sweep line • Sweep the plane with a vertical line from left to right and stop at event points a) Left endpoint: add segment to T b) Right endpoint: remove segment from T c) V-segment: report intersections with H-segments stored in T.

Analysis • Sorting: • O(nlogn) • Add/delete from T • O(logn) per operation • O(nlogn) total • Processing V-segments • O(logn) per segment endpoints • O(kv) where kv is number of intersections with v • O(nlogn + k) total • Overal: O(nlogn + k)

The “General” Case • Assumption: All coordinates of endpoints and intersections are distinct • In particular: • No vertical segments • No three segments intersect at one point • These cases can be handled with special care.

Sweep Line • Invariant (as before): all intersections on the left of the sweep line have been already reported • Stops at all “important” x-coordinates. i. e. at left endpoints, at right endpoints, and at intersection points • Do not know the intersection in advance. • The list of important x-coordinates is constructed and maintained dynamically

Sweep Line • Also need to maintain the information about the segments intersecting the sweep line • Cannot keep the values of y-coordinates of the segments • Instead we will maintain their order, i. e. at any points, we maintain all segments intersecting the sweep line, sorted by the y-coordinates of the intersections L

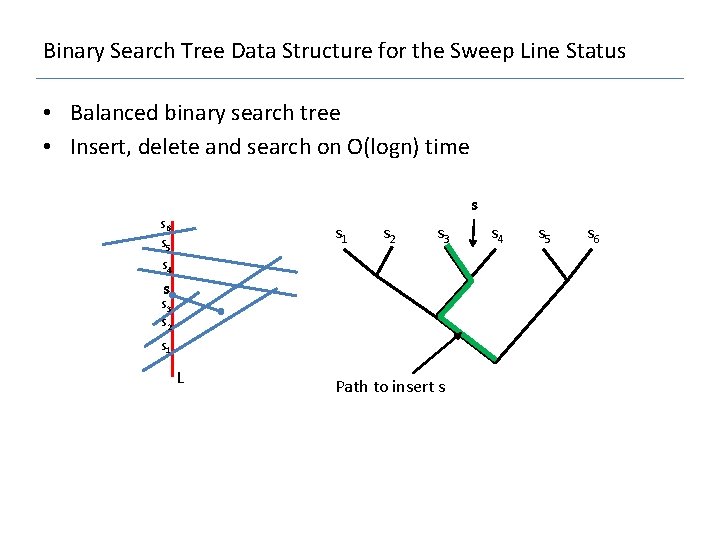
Binary Search Tree Data Structure for the Sweep Line Status • Balanced binary search tree • Insert, delete and search on O(logn) time s s 6 s 5 s 1 s 2 s 3 s 4 s s 3 s 2 s 1 L Path to insert s s 4 s 5 s 6

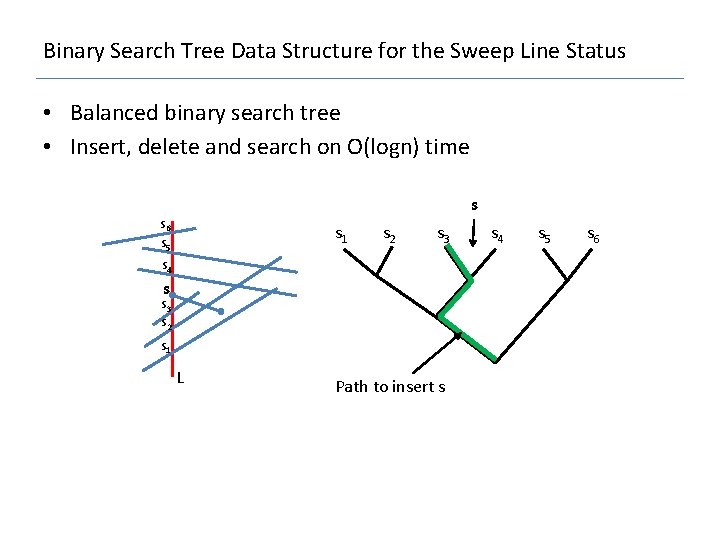
Binary Search Tree Data Structure for the Sweep Line Status • Balanced binary search tree • Insert, delete and search on O(logn) time s s 6 s 5 s 1 s 2 s 3 s 4 s s 3 s 2 s 1 L Path to insert s s 4 s 5 s 6

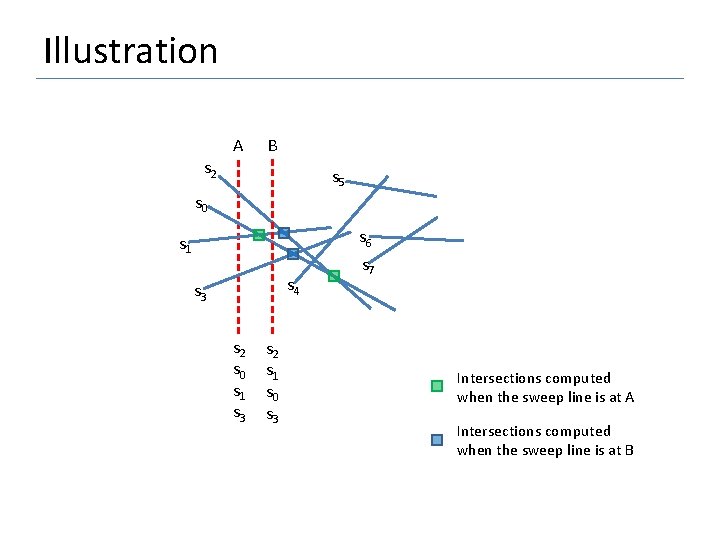
Illustration A s 2 B s 5 s 0 s 6 s 1 s 4 s 3 s 2 s 0 s 1 s 3 s 2 s 1 s 0 s 3 s 7 Intersections computed when the sweep line is at A Intersections computed when the sweep line is at B

Algorithm Could… • { update T} • For each pair of neighbors s and s’ in T: • Check if s and s’ intersect on the right side of the sweep line • If so, add their intersection to Q • Remove the possible duplicate in Q • Until Q is empty

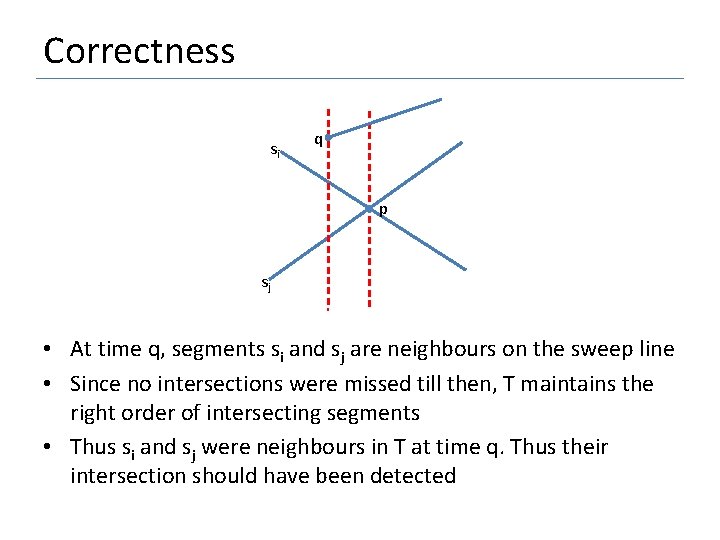
Correctness • Algorithm only checks intersections between segments that are adjacent along the sweep line at some point • The algorithm obviously does not report false intersections • But can it miss any intersections? • No. If segments si and sj intersect at point p, si and sj are neighbors just before the sweep line reaches p. • Proof: • Let p be the leftmost unreported intersection • Let q be the last event before p

Correctness si q p sj • At time q, segments si and sj are neighbours on the sweep line • Since no intersections were missed till then, T maintains the right order of intersecting segments • Thus si and sj were neighbours in T at time q. Thus their intersection should have been detected

Algorithm • T : Binary search tree sorting the sweep line status • Q: even queue • Initiate T to empty • Initialize Q ( to contain segment endpoints stored by x-coordinates) • Repeat • Take the next “event” p from Q • {update T} • If p is the left endpoint of a segment, add p to T; update Q • If p is the right endpoint of a segment, delete p from T; update Q • If p is the intersection point of s and s’, swap the order of s and s’ in T and report p; update Q

Analysis • Initializing Q : O(nlogn) • Updating T: • O(logn) per operation • O(nlogn + klogn) total • Updating Q • O(logn) per intersection • O(nlogn + klogn) total • Overal O(nlogn + klogn) time • Storate Space: O(n)