Sediment Transport Whenever water flows in a channel

Sediment Transport Whenever water flows in a channel it tries to scour its surface. Silt, gravel and large boulders detached from the bed or sides of the channel. These detached particles are swept downstream by moving water. This phenomena known as sediment transport.

Sediment Transport Importance of sediment transport i) Poorly designed artificial channels get silted up so badly that they soon become inoperable causing huge loss to public exchequer. ii) Flood control scheme chiefly depends on peak flood levels which in turn depends up on scour and deposition of sediment. The bed level changes with scour and silt deposition thereby changing its flood levels.

Sediment Transport Importance of sediment transport iii) The storage capacity of the reservoir is reduced by silting thereby reducing its use and life. Sediment Load It’s a burden to be borne by flowing water. Bed load: In this sediment moves along the bed with occasional jumps into the channel. Suspended load: In this, material is maintained in suspension due to turbulence of the flowing water.

Sediment Transport Bed formation Channel bed made of fine sand(lesser than 2 mm dia. ) When sediment load comes to motion that stage is termed as threshold stage of motion. On further increase of velocity the bed develops ripples of the saw tooth type. As the velocity increased further larger periodic irregularities appear and are called dunes. Dunes may form but ripples do no occur if size of bed particles is coarser than 0. 6 mm.

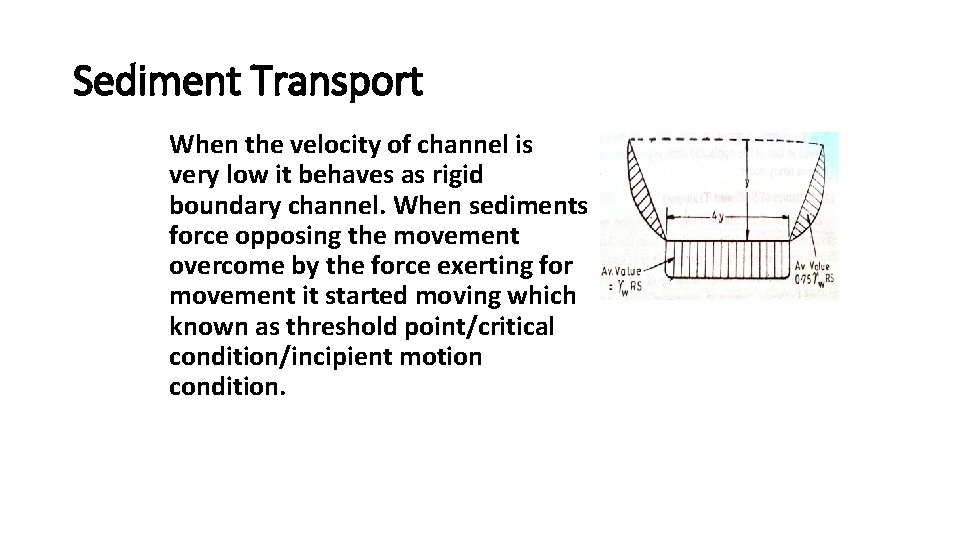
Sediment Transport Mechanics of sediment transport Assume soil is incoherent i. e. c = 0 It may be noted that the unit tractive force in channels except for wide open channls is not uniformally distributed along the wetted perimeter.

Sediment Transport When the velocity of channel is very low it behaves as rigid boundary channel. When sediments force opposing the movement overcome by the force exerting for movement it started moving which known as threshold point/critical condition/incipient motion condition.

Sediment Transport Design of non scouring channels having protected side slopes in alluviums

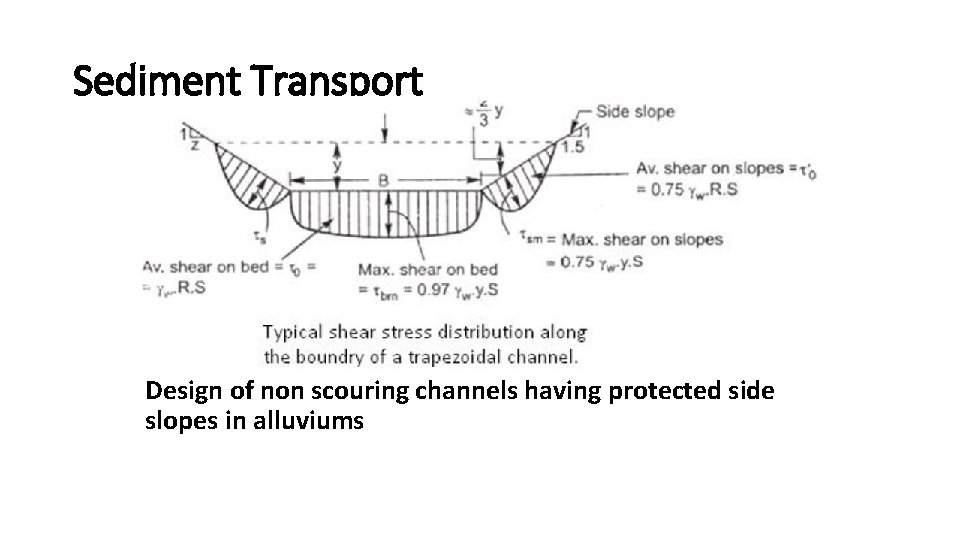
Sediment Transport Design of non scouring channels having unprotected side slopes in alluviums.

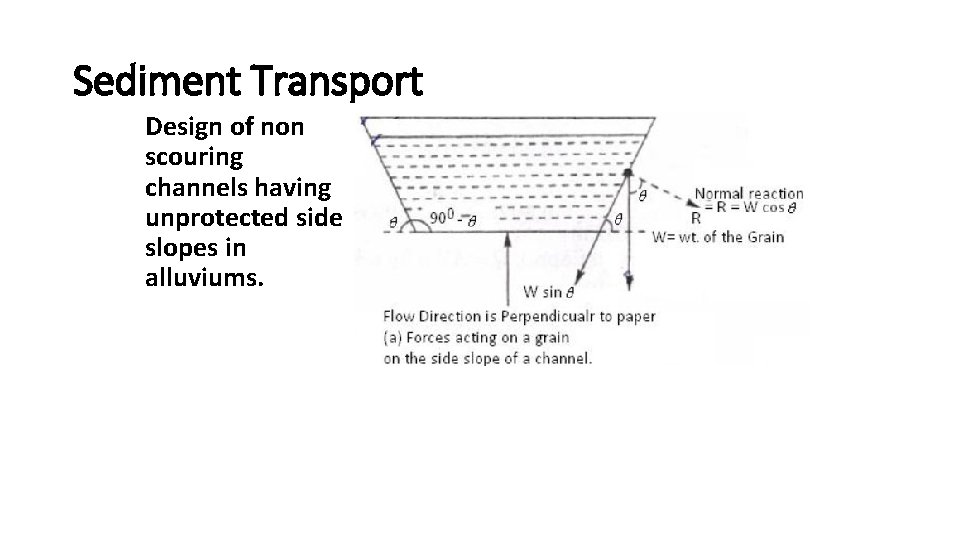
Sediment Transport Angle of repose: maximum angle at which an object can rest on an inclined plane without sliding down. This angle is equal to the arctangent of the coefficient of static friction μs between the surfaces. Arctangent: y = arctan(x) here x = tan(y)

Sediment Transport Let represents the critical shear stress or the shear stress required to move a similar grain on a horizontal bed, as shown in The above equation shows that which means that the shear stress required to move a grain on the side slopes is less than the shear stress required to move the grain on canal bed.

Sediment Transport The average value of actual shear stress generated by the flowing water in a channel of given R and S is and on the side slopes this value is 0. 75 time av. Shear stress on bed.

Sediment Transport Design of stable channels in India As long as av. Shear stress acting on the boundary of an alluvial channel is less than critical shear stress the channel shape remains unchanged and hence the channel boundaries considered as rigid boundary. The resistance equations of chezy’s and manning’s formula remain applicable to such channels. Stable and regime channels: Those canals designed for not scouring and silting. In artificial channels it can be attained but not in rivers.

Sediment Transport Kennedy Theory: He concluded that the silt supporting power in a channel cross section was mainly dependent upon the generation of the eddies, rising to the surface. These eddies are generated due to the friction of the flowing water with the channel surface, the vertical component of these eddies try to move the sediment up, while the weight of the sediment tries to bring it down, thus keeping the sediment in suspension. So if the velocity is sufficient to generate these eddies, so as to keep the sediment just in suspension, silting will be avoided based upon this concept, he defined he critical velocity (Vo) in a channel as the mean velocity which will just keep the channel free form silting or scouring, and related it to the depth of flow by the equation.

Sediment Transport Where Vo = critical velocity in the channel in m/s y = water depth in channel in m m = C. V. R.

Sediment Transport Design procedure: 1. Determine the critical velocity Vo by assuming a trail depth, and then determine area by dividing discharge by velocity. 2. Determine channel dimensions. 3. Finally, compute the actual mean velocity (V) that will prevail in the channel of this cross section, , by using Kutter’s formula, manning’s formula, etc. if the two velocity’s Vo and V work out to be the same, then the assumed depth is all right, otherwise change it and repeat the procedure till V and Vo become equal.

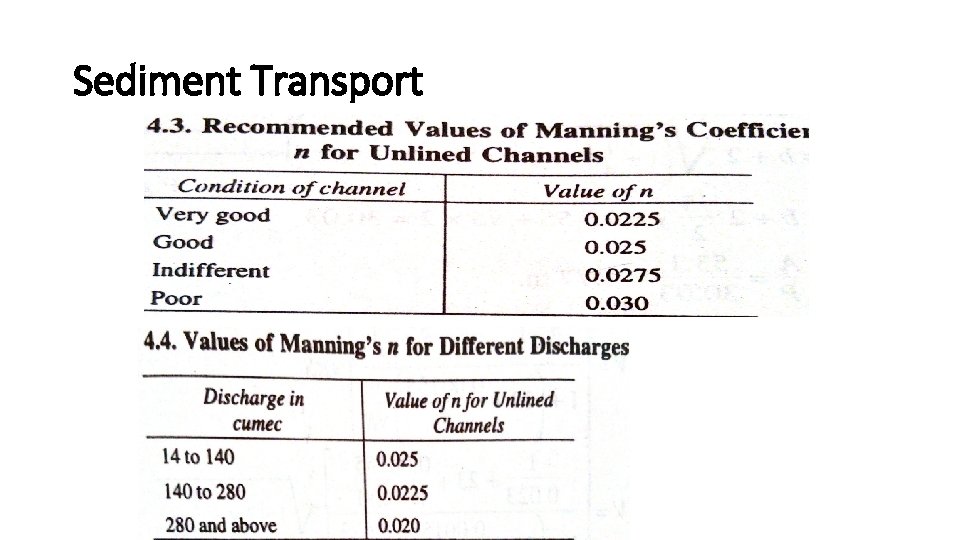
Sediment Transport Where V = velocity of flow in meteres/sec R = Hydraulic mean depth in meters. S= Bed slope of the channel. n = Rugosity coefficient

Sediment Transport

Sediment Transport Where C = constant depending up on shape and surface of the channel. Kutter’s equation is mostly used with kennedy’s theory for actual mean velocity calculation.

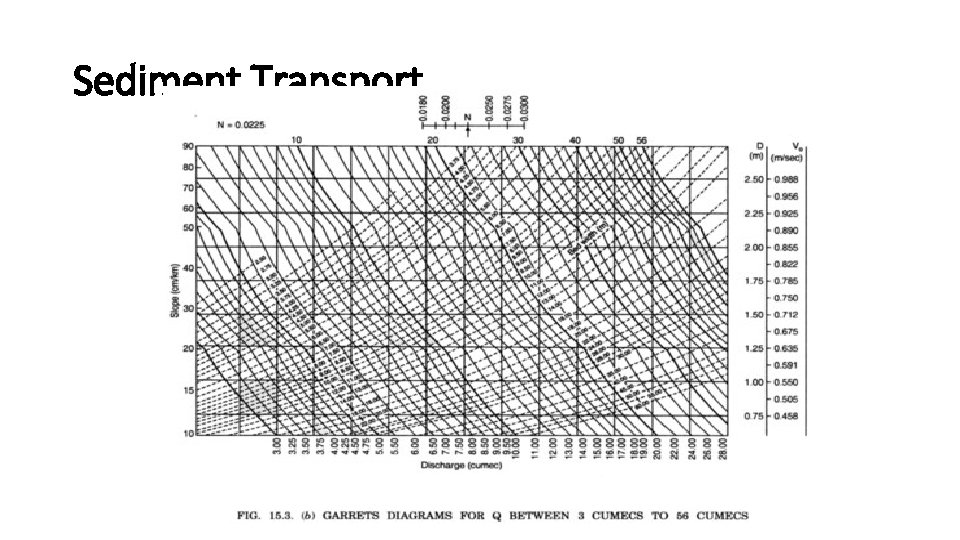
Sediment Transport Use of Garret's Diagrams for Applying Kennedy's Theory. Graphical solution of Kennedy's and Kutter's equations, was evolved by Garret. The original diagrams given by him were in F. P. S. system, but here they have been changed into M. K. S. /S. I. system Procedure:

Sediment Transport (i) (iii) (iv) (v) The discharge, bed slope, rugosity coefficient, value of C. V. R. is given for the channel to be designed. Find out the point of intersection of the given slope line and discharge curve. At this point of intersection, draw a vertical line intersecting the various bed width curves. For different bed widths (B), the corresponding values of water depth (y) and critical velocity (Vo) can be read on the right hand ordinate. Each such pair of bed width (B) and depth (y) will satisfy Kutter's equation, and is capable of carrying the required discharge at the given slope and rugosity coefficient. Choose one such pair and determine the actual velocity of flow Determine the critical velocity ratio (V/Vo) taking V as calculated and VQ as read. If the value of C. V. R. is not the same as given in question, repeat the procedure with other pairs of B and y.

Sediment Transport

Sediment Transport Lacey found many drawbacks in Kennedy's Theory (1895). Lacey's regime channels : It was stated by Kennedy that a channel is said to be in a state of 'regime' if there is neither silting nor scouring in the channel. But Lacey came out with the statement that even a channel showing no silting no scouring may actually not be in regime. He, therefore, differentiated between three regime conditions.

Sediment Transport (i) True regime (ii) Initial regime (iii) Final regime. True regime: A channel shall be in regime, if there is neither silting nor scouring. Initial regime: When only the bed slope of a channel varies due to dropping of silt, and its cross-section or wetted perimeter remains unaffected, even the channel can exhibit 'no silting no scouring' properties, called Initial regime.

Sediment Transport Final regime: If there is no resistance from the sides, and all the variables such as perimeter, depth, slope, etc. are equally free to vary and finally get adjusted according to discharge and silt grade, then the channel is said to have achieved permanent stability, called final regime. Design procedure for Lacey’s theory (1) Calculate the velocity from equation.

Sediment Transport Where Q is in cumecs : V is in m/s ; and f is the silt factor given by where dmm = Average particle size in mm, as given in

Sediment Transport (1) Table Values of particle size (dmm) for various types of alluvial materials for use in

Sediment Transport (2) Work out the hydraulic mean depth (R) from (3) Compute area of channel section

Sediment Transport 4. Compute wetted perimeter Q = M 3/sec 5. Knowing these values, the channel section is known; and finally the bed slope S is determined by the equation

Sediment Transport Where f is the silt factor, given by Q is the discharge in cumec.

Sediment Transport • The concept of silt transportation is same in both the cases, both agree that the silt is carried by the vertical eddies generated due to friction of the flowing water against rough surface of canal. Kennedy considered a trapezoidal channel section and, therefore, he neglected eddies generated from the sides. For this reason, Kennedy's critical velocity formula was derived only in terms of depth of flow(y). Lacey considered that an irrigation channel achieves a cup-shaped section(semi-ellipse) and that entire wetted perimeter of the channel contributes to the generation of silt supporting eddies. He, thus, used hydraulic mean radius(R) as a variable in his regime velocity formulas instead of depth(y). • Kennedy stated all the channels to be in state of regime provided they did not silt or scour. But Lacey differentiated between two regime conditions, i. e. initial regime and final regime. • According to Lacey, grain size of material forming the channel is an important factor, and should need much more attention than what was given to it by Kennedy. He connected grain size(d) with his silt factor(f) as f= 1. 76(dmm)^0. 5.

Sediment Transport • Kennedy used Kutter's formula for determining actual generated channel velocity. The value of Kutter's rugosity coefficient(n) is again a guess work. Lacey, on the other hand, has produced a general regime flow, after analyzing huge data on regime channels. • Kennedy has not given any importance to bed width and depth ratio. Lacey has connected wetted perimeter(P) as well as area(A) of the channel with discharge, thus, establishing a fixed relationship between bed width and depth. • Kennedy did not fix regime slopes for his channels, although, his diagrams indicate that steeper slopes are required for smaller channels and flatter slopes are required for larger channels. Lacey, on the other hand, has fixed the regime slope, connecting it with discharge.

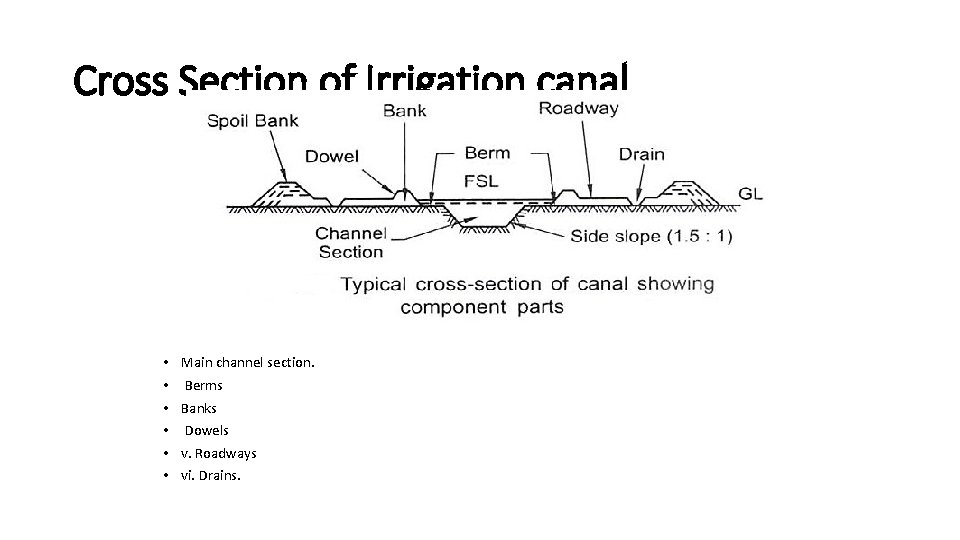
Cross Section of Irrigation canal • • • Main channel section. Berms Banks Dowels v. Roadways vi. Drains.