Security Architecture Analysis Lecture 2 Reasoning About System

Security Architecture Analysis: Lecture 2 • Reasoning About System Architectures • Box Structure Reasoning for Components Black boxes State boxes • Compositional Reasoning for Networks
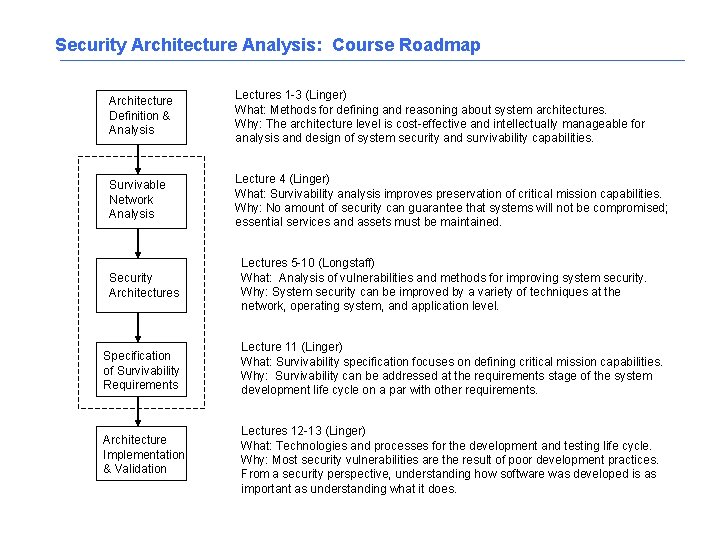
Security Architecture Analysis: Course Roadmap Architecture Definition & Analysis Lectures 1 -3 (Linger) What: Methods for defining and reasoning about system architectures. Why: The architecture level is cost-effective and intellectually manageable for analysis and design of system security and survivability capabilities. Survivable Network Analysis Lecture 4 (Linger) What: Survivability analysis improves preservation of critical mission capabilities. Why: No amount of security can guarantee that systems will not be compromised; essential services and assets must be maintained. Security Architectures Lectures 5 -10 (Longstaff) What: Analysis of vulnerabilities and methods for improving system security. Why: System security can be improved by a variety of techniques at the network, operating system, and application level. Specification of Survivability Requirements Lecture 11 (Linger) What: Survivability specification focuses on defining critical mission capabilities. Why: Survivability can be addressed at the requirements stage of the system development life cycle on a par with other requirements. Architecture Implementation & Validation Lectures 12 -13 (Linger) What: Technologies and processes for the development and testing life cycle. Why: Most security vulnerabilities are the result of poor development practices. From a security perspective, understanding how software was developed is as important as understanding what it does.

Reasoning About System Architectures • It is vital in analyzing security and survivability (and other system properties) to know how to reason about system architectures “Reasoning” means: Inferring from available information what architectures and their components do and how they do it Knowing what constitutes complete definitions and what information is missing • Reasoning requires mental models for components and architectures • Models have formal basis, but are effective when applied informally • We will use the models in an informal way Know what questions to ask about architectures

Box Structure Reasoning for Components • Box Structures A systematic model for component analysis and design Five fundamental component characteristics (BURST) Boundary: What is inside and what is outside? Users: Who are the users? Responses: What is the set of possible responses? Stimuli: What is the set of possible stimuli? Technology: What is the hardware/software employed? Three fundamental component representations: Black box: State Box: Clear box: External behavior view of a component Retained data view of a component Procedural view of a component (another course!)
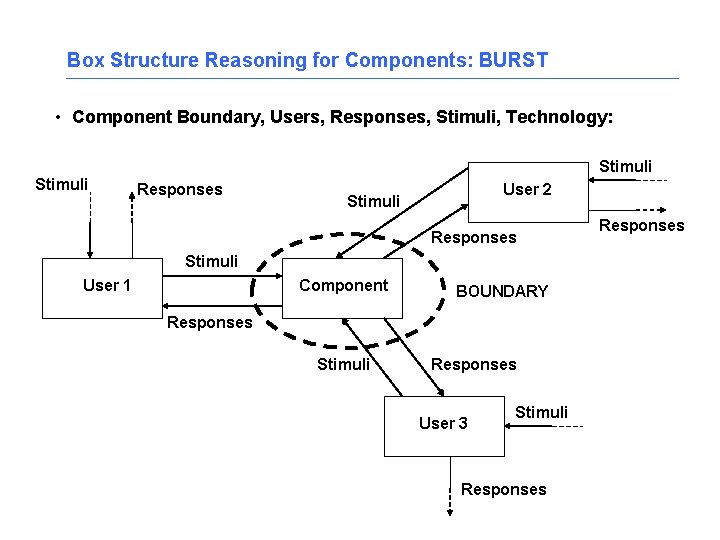
Box Structure Reasoning for Components: BURST • Component Boundary, Users, Responses, Stimuli, Technology: Stimuli Responses User 2 Stimuli Responses Stimuli User 1 Component BOUNDARY Responses Stimuli Responses User 3 Stimuli Responses
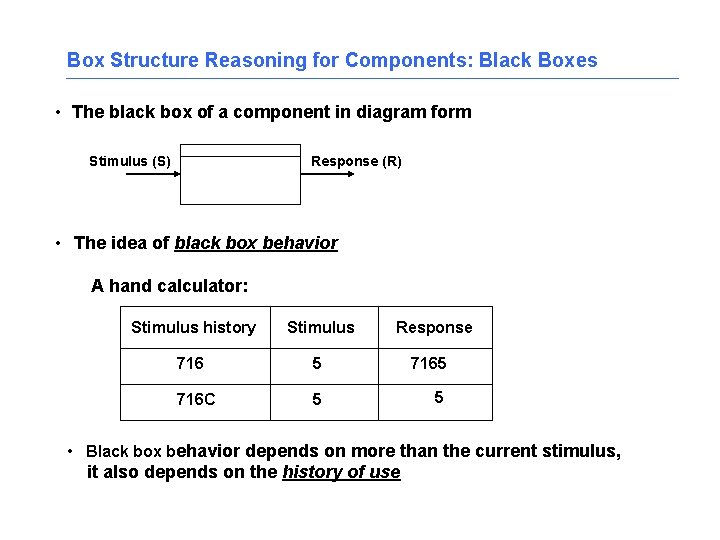
Box Structure Reasoning for Components: Black Boxes • The black box of a component in diagram form Stimulus (S) Response (R) • The idea of black box behavior A hand calculator: Stimulus history Stimulus Response 716 5 716 C 5 5 • Black box behavior depends on more than the current stimulus, it also depends on the history of use

Box Structure Reasoning for Components: Black Boxes • Transition function of a black box (stimulus history, stimulus) --> (response, new stimulus history) • Accumulating hand calculator stimulus history (SH) through black box transitions: Stimulus History Response New Stimulus History C 1 4 + 4 3 = C * C C 14+4 C 14+43= 0 1 14 14 4 43 57 0 C C 14+4 C 14+43= * • Partial transition function of a simple hand calculator (valid arithmetic expression, =) --> (expression value, = appended to SH)

Box Structure Reasoning for Components: Black Boxes • Transition function of “Add 2” black box Response is sum of last two stimuli: R = S(I) + S(I -1) • Transition function of “Max 2” black box Response is maximum of last two stimuli: R = max(S(I), S(I -1)) • Black box transition function of Microsoft Word Difficult to write down, but conceptually no different Can be reasoned about in terms of stimuli and stimulus histories

Box Structure Reasoning for Components: Black Boxes • Black box transition function of a simple authentication server Stimulus Add authentication data for user xyz ID claim and evidence Condition on SH none Response “OK” xyz data present in SH, does not match evidence “access denied” xyz data present in SH, and matches evidence “access granted” • Black box definitions can be complete: Define required behavior in all possible circumstances of use (Almost never done, but invaluable)

Box Structure Reasoning for Components: Black Boxes • A black box definition deals only with visible external behavior It is state-free and procedure-free It is the user view: requirements and specifications • Any deterministic component exhibits black box behavior Reasoning with the black box model Understand BURST Given a stimulus, consider possible conditions on the stimulus history to determine possible responses First question to ask to understand how a component will respond to a stimulus: What is the history of use?

Box Structure Reasoning for Components: Black Boxes • Black box reasoning for a data base system (implied BURST) What is the response, given this stimulus: Delete a record Add a record Update a record Create a report of all employees with at least 10 years experience who are earning less than 50 K • What do you want the behavior to be?

Box Structure Reasoning for Components: Black Boxes • Black box reasoning for a virus checker on an email server (implied BURST) What is the response, given this stimulus: An input email message that contains a virus An input email message that does not contain a virus • What do you want the behavior to be?

Box Structure Reasoning for Components: Black Boxes • Black box reasoning for a firewall on an email server (implied BURST) What is the response, given this stimulus: An input email message with a file attachment • What do you want the behavior to be?
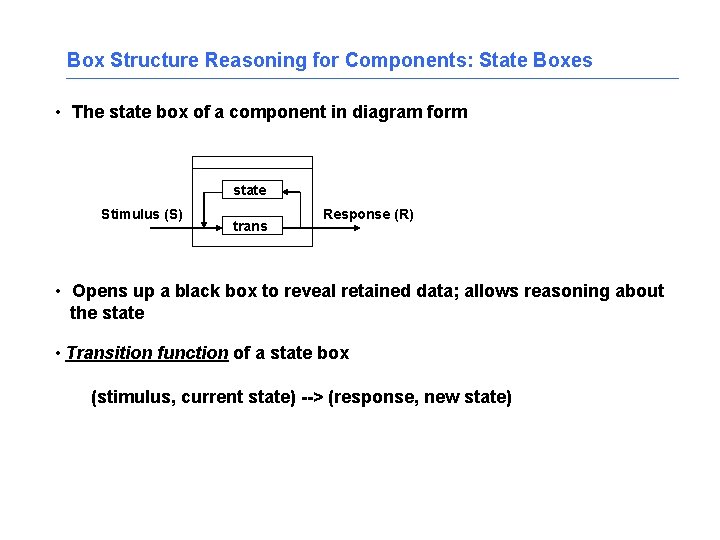
Box Structure Reasoning for Components: State Boxes • The state box of a component in diagram form state Stimulus (S) trans Response (R) • Opens up a black box to reveal retained data; allows reasoning about the state • Transition function of a state box (stimulus, current state) --> (response, new state)
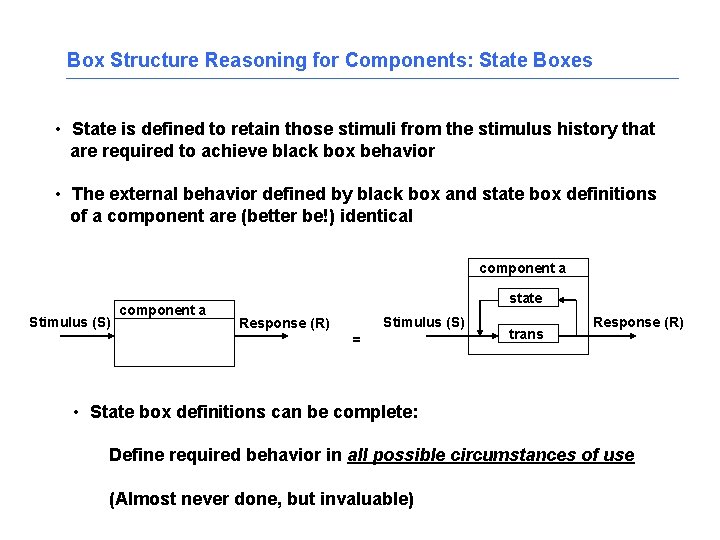
Box Structure Reasoning for Components: State Boxes • State is defined to retain those stimuli from the stimulus history that are required to achieve black box behavior • The external behavior defined by black box and state box definitions of a component are (better be!) identical component a Stimulus (S) component a state Stimulus (S) Response (R) = trans Response (R) • State box definitions can be complete: Define required behavior in all possible circumstances of use (Almost never done, but invaluable)

Box Structure Reasoning for Components: State Boxes • Transition function of “Add 2” • The state box of “Add 2” Add 2 R : = S + L (compute response) L : = S (update state) L S trans R • The state box of “Max 2” • Transition function of “Max 2” Max 2 R : = max(S, K) (compute response) K : = S (update state) K S trans R • State box transition function of Microsoft Word Difficult to write down, but conceptually no different Can be reasoned about in terms of stimuli and states

Box Structure Reasoning for Components: State Boxes • State box reasoning for a virus checker on an email server (implied BURST and state) What is the response, given this stimulus: An input email message that contains a virus An input email message that does not contain a virus

Box Structure Reasoning for Components: State Boxes • State box reasoning for a firewall on an email server (implied BURST and state) What is the response, given this stimulus: An input email message with a file attachment

Box Structure Reasoning for Components: Netting It Out • Rigorous model that can be applied informally in thinking about what components do and how they do it • Reasoning about behavior at black box level Understand BURST Given a stimuli, response depends on history of use • Reasoning about behavior at state box level Understand BURST Given a stimuli, response depends on current state “Oh, yes, the abc vendor’s firewall (or authentication server, or encryption algorithm, or whatever) exhibits black box behavior, and can also be reasoned about as a state box. ”
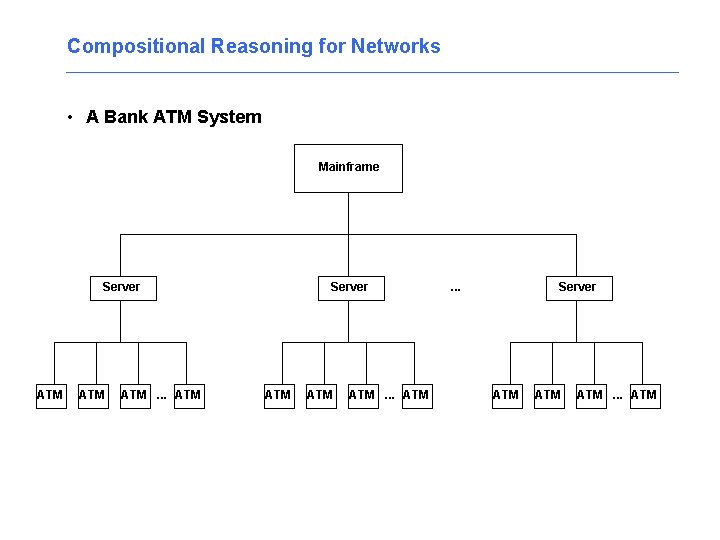
Compositional Reasoning for Networks • A Bank ATM System Mainframe Server ATM ATM ATM. . . ATM . . . Server ATM ATM. . . ATM

Compositional Reasoning for Networks • What happens from viewpoint of ATM user submitting a transaction? User ATM Server Mainframe Server ATM User [User] o [ATM] o [server] o [mainframe] o [server] o [ATM] o [User] “o” is composition operator “[, ]” denote the transition function of the component Note that each use of a component is in the composition • Simple compositions of components look like pipeline architectures • ATM Security: Composition with wrong pin number (U for user) U ATM U Server U Try again ATM U wrong pin Server U ATM Access denied U

Compositional Reasoning for Networks • Another pin number composition U right pin U ATM U wrong pin Server U Try again ATM U wrong pin Server U ATM U Access granted Server U ATM U Access denied • Compositional reasoning is concerned with the net effect of all the components in a composition • Net effect means the overall change From the stimuli to the first component To the response from the last component
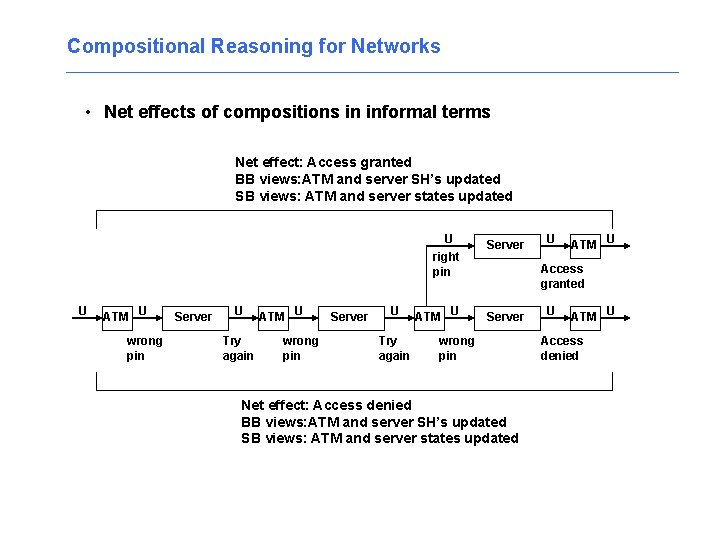
Compositional Reasoning for Networks • Net effects of compositions in informal terms Net effect: Access granted BB views: ATM and server SH’s updated SB views: ATM and server states updated U ATM U wrong pin Server U Try again U right pin Server ATM U Server U ATM U Access granted wrong pin Net effect: Access denied BB views: ATM and server SH’s updated SB views: ATM and server states updated U ATM U Access denied
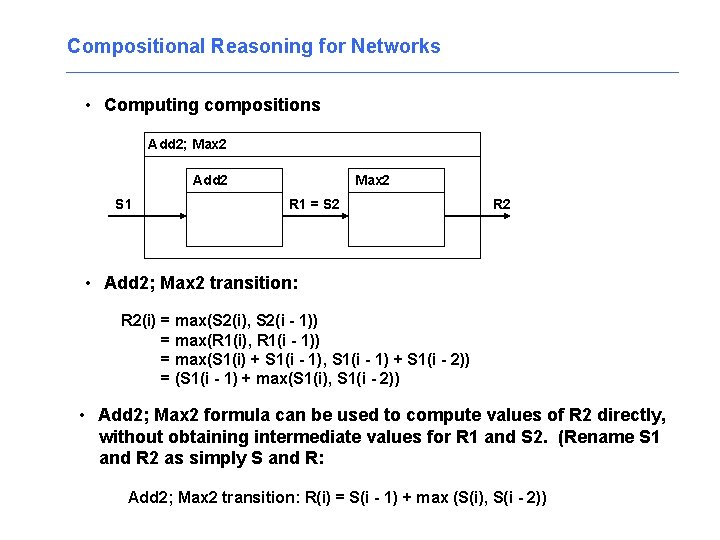
Compositional Reasoning for Networks • Computing compositions Add 2; Max 2 Add 2 S 1 Max 2 R 1 = S 2 R 2 • Add 2; Max 2 transition: R 2(i) = max(S 2(i), S 2(i - 1)) = max(R 1(i), R 1(i - 1)) = max(S 1(i) + S 1(i - 1), S 1(i - 1) + S 1(i - 2)) = (S 1(i - 1) + max(S 1(i), S 1(i - 2)) • Add 2; Max 2 formula can be used to compute values of R 2 directly, without obtaining intermediate values for R 1 and S 2. (Rename S 1 and R 2 as simply S and R: Add 2; Max 2 transition: R(i) = S(i - 1) + max (S(i), S(i - 2))
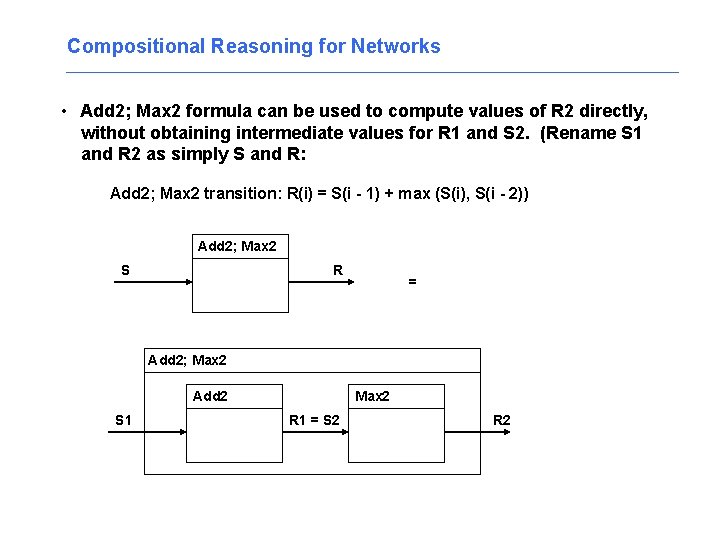
Compositional Reasoning for Networks • Add 2; Max 2 formula can be used to compute values of R 2 directly, without obtaining intermediate values for R 1 and S 2. (Rename S 1 and R 2 as simply S and R: Add 2; Max 2 transition: R(i) = S(i - 1) + max (S(i), S(i - 2)) Add 2; Max 2 S R = Add 2; Max 2 Add 2 S 1 Max 2 R 1 = S 2 R 2
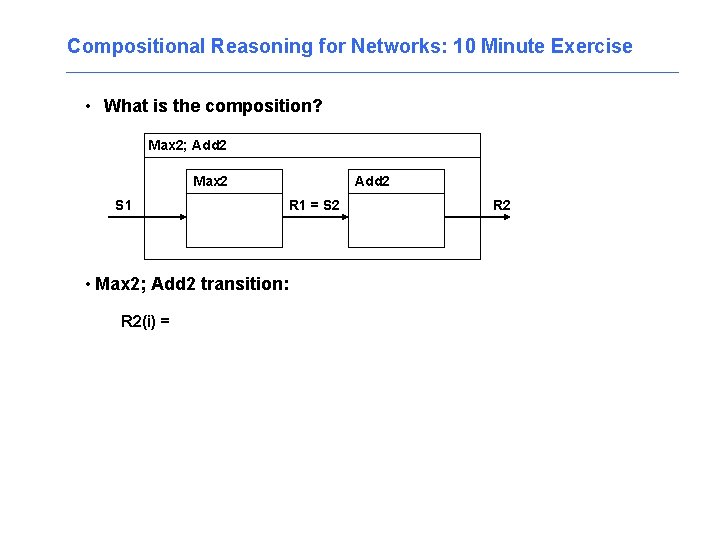
Compositional Reasoning for Networks: 10 Minute Exercise • What is the composition? Max 2; Add 2 Max 2 S 1 • Max 2; Add 2 transition: R 2(i) = Add 2 R 1 = S 2 R 2
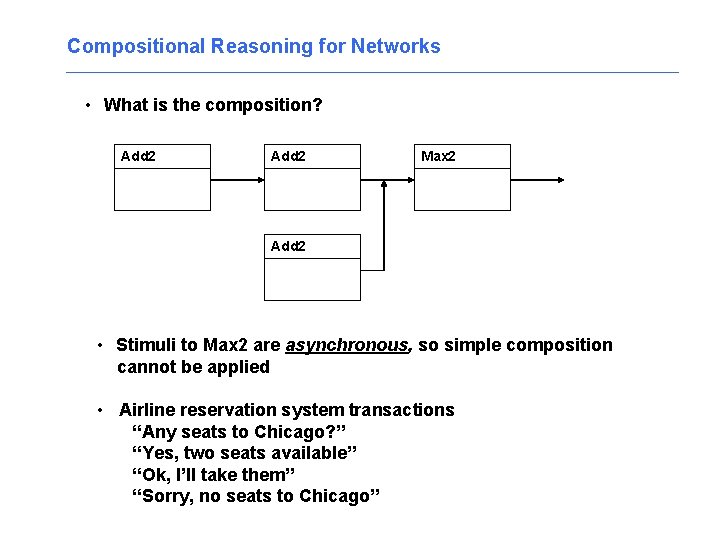
Compositional Reasoning for Networks • What is the composition? Add 2 Max 2 Add 2 • Stimuli to Max 2 are asynchronous, so simple composition cannot be applied • Airline reservation system transactions “Any seats to Chicago? ” “Yes, two seats available” “Ok, I’ll take them” “Sorry, no seats to Chicago”
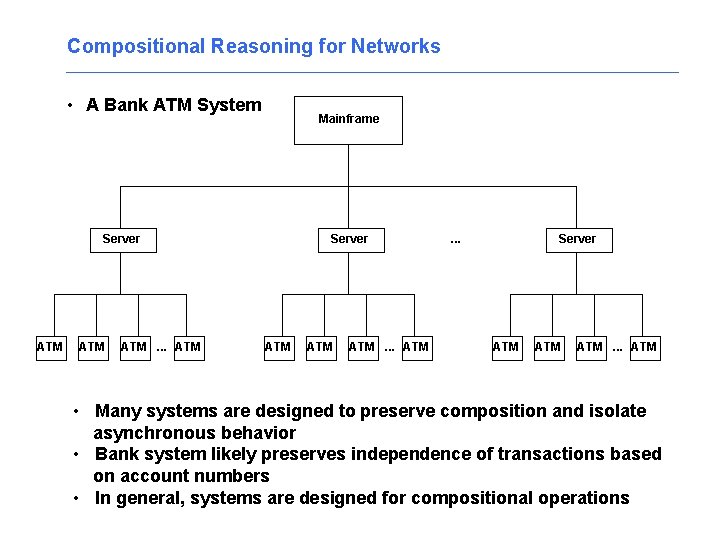
Compositional Reasoning for Networks • A Bank ATM System Mainframe Server ATM ATM ATM. . . ATM . . . Server ATM ATM. . . ATM • Many systems are designed to preserve composition and isolate asynchronous behavior • Bank system likely preserves independence of transactions based on account numbers • In general, systems are designed for compositional operations
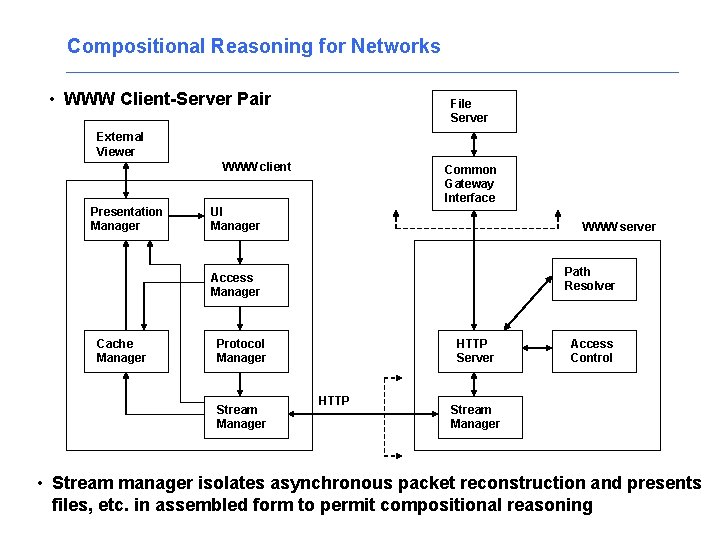
Compositional Reasoning for Networks • WWW Client-Server Pair File Server External Viewer WWW client Presentation Manager Common Gateway Interface UI Manager WWW server Path Resolver Access Manager Cache Manager Protocol Manager Stream Manager HTTP Server HTTP Access Control Stream Manager • Stream manager isolates asynchronous packet reconstruction and presents files, etc. in assembled form to permit compositional reasoning
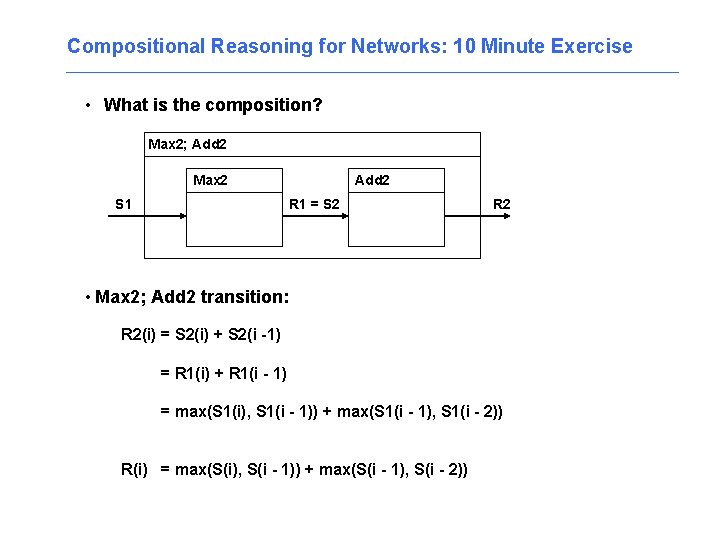
Compositional Reasoning for Networks: 10 Minute Exercise • What is the composition? Max 2; Add 2 Max 2 S 1 Add 2 R 1 = S 2 R 2 • Max 2; Add 2 transition: R 2(i) = S 2(i) + S 2(i -1) = R 1(i) + R 1(i - 1) = max(S 1(i), S 1(i - 1)) + max(S 1(i - 1), S 1(i - 2)) R(i) = max(S(i), S(i - 1)) + max(S(i - 1), S(i - 2))
- Slides: 30