Sections 3 and 4 CHAPTER 1 An angle

Sections 3 and 4 CHAPTER 1

An angle is a figure formed by two rays, or sides, with a common endpoint called the vertex (plural: vertices). You can name an angle several ways: by its vertex, by a point on each ray and the vertex, or by a number.

The set of all points between the sides of the angle is the interior of an angle. The exterior of an angleis the set of all points outside the angle. Angle Name R, SRT, TRS, or 1 You cannot name an angle just by its vertex if the point is the vertex of more than one angle. In this case, you must use all three points to name the angle, and the middle point is always the vertex.

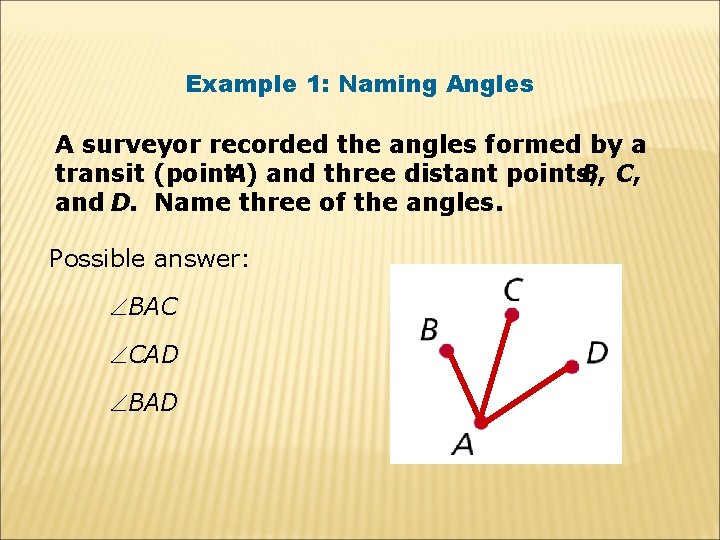
Example 1: Naming Angles A surveyor recorded the angles formed by a transit (point. A) and three distant points, B, C, and D. Name three of the angles. Possible answer: BAC CAD BAD

Check It Out! Example 1 Write the different ways you can name the angles in the diagram. RTQ, T, STR, 1, 2

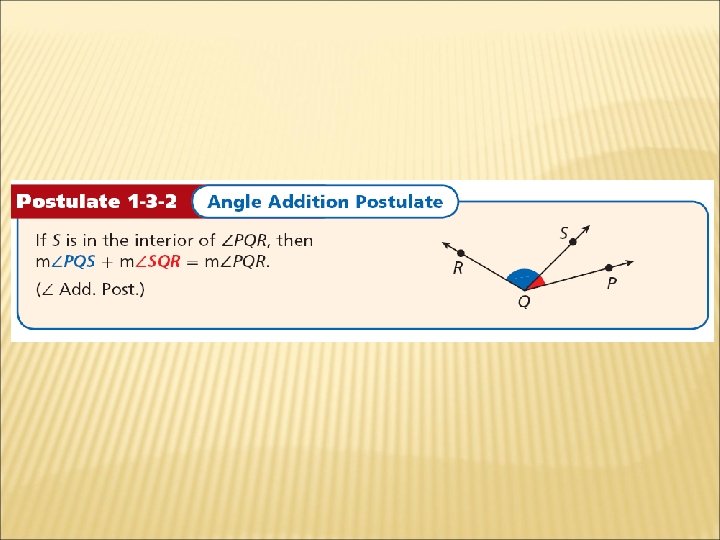
The measureof an angle is usually given in degrees. Since there are 360° in a circle, one degree is of a circle. When you use a protractor to measure angles, you are applying the following postulate.

Example 2: Measuring and Classifying Angles Find the measure of each angle. Then classify each as acute, right, or obtuse. A. WXV m WXV = 30° WXV is acute. B. ZXW m ZXW = |130° - 30°| = 100° ZXW = is obtuse.

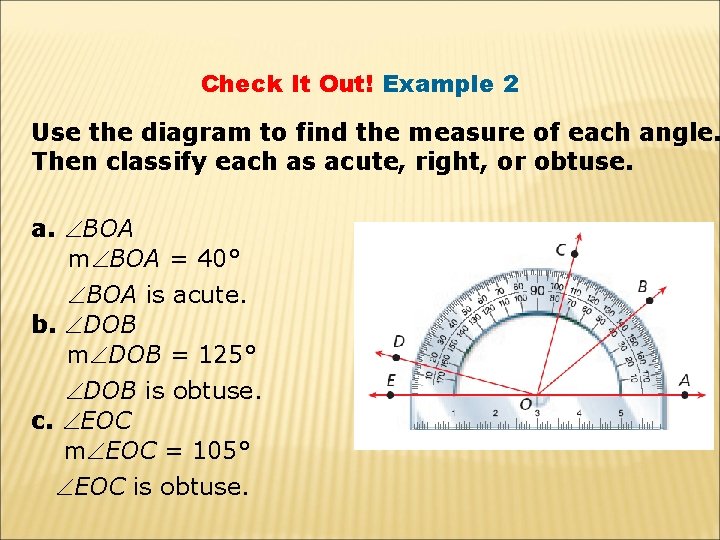
Check It Out! Example 2 Use the diagram to find the measure of each angle. Then classify each as acute, right, or obtuse. a. BOA m BOA = 40° BOA is acute. b. DOB m DOB = 125° DOB is obtuse. c. EOC m EOC = 105° EOC is obtuse.

Congruent anglesare angles that have the same measure. In the diagram, m ABC = m DEF, so you can write ABC DEF. This is read as “angle ABC is congruent to angle DEF. ” Arc marks are used to show that the two angles are congruent.

Example 3: Using the Angle Addition Postulate m DEG = 115°, and m DEF = 48°. Find m FEG m DEG = m DEF + m FEG Add. Post. 115 = 48 + m FEG Substitute the given values. – 48° Subtract 48 from both sides. 67 = m FEG Simplify.

An angle bisectoris a ray that divides an angle into two congruent angles. JK bisects LJM; thus LJK KJM.

Example 4: Finding the Measure of an Angle KM bisects JKL, m JKM = (4 x + 6)°, and m MKL = (7 x – 12)°. Find m JKM.

Example 1 A: Identifying Angle Pairs Tell whether the angles are only adjacent, adjacent and form a linear pair, or not adjacent. AEB and BED have a common vertex, E, a common side, EB, and no common interior points. Their noncommon sides, EA and ED, are opposite rays. Therefore, AEB and BED are adjacent angles and form a linear pair.

Check It Out! Example 1 a Tell whether the angles are only adjacent, adjacent and form a linear pair, or not adjacent. 5 and 6 are adjacent angles. Their noncommon sides, EA and ED, are opposite rays, so 5 and 6 also form a linear pair.

You can find the complement of an angle that measures x° by subtracting its measure from 90°, or (90 – x)°. You can find the supplement of an angle that measures x° by subtracting its measure from 180°, or (180 – x)°.

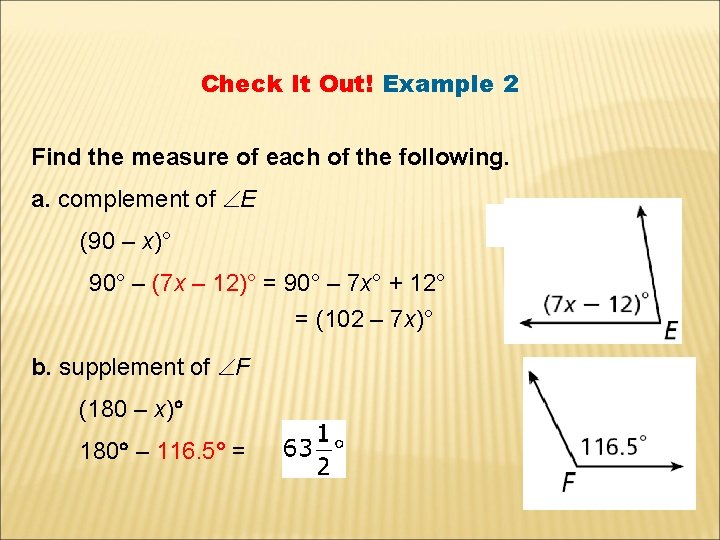
Check It Out! Example 2 Find the measure of each of the following. a. complement of E (90 – x)° 90° – (7 x – 12)° = 90° – 7 x° + 12° = (102 – 7 x)° b. supplement of F (180 – x) 180 – 116. 5° =

Example 3: Using Complements and Supplements to Solve Problems An angle is 10° more than 3 times the measure of its complement. Find the measure of the complement. Step 1 Let m A = x°. Then B, its complement measures (90 – x)°. Step 2 Write and solve an equation. x = 3(90 – x) + 10 Substitute x for m A and 90 – x for m B. x = 270 – 3 x + 10 Distrib. Prop. x = 280 – 3 x Combine like terms. 4 x = 280 Divide both sides by 4. x = 70 Simplify. The measure of the complement, B, is (90 – 70) = 20.

Example 4: Problem-Solving Application Light passing through a fiber optic cable reflects off the walls of the cable in such a way that 1 ≅ 2, 1 and 3 are complementary, and 2 and 4 are complementary. If m 1 = 47°, find m 2, m 3, and m 4.

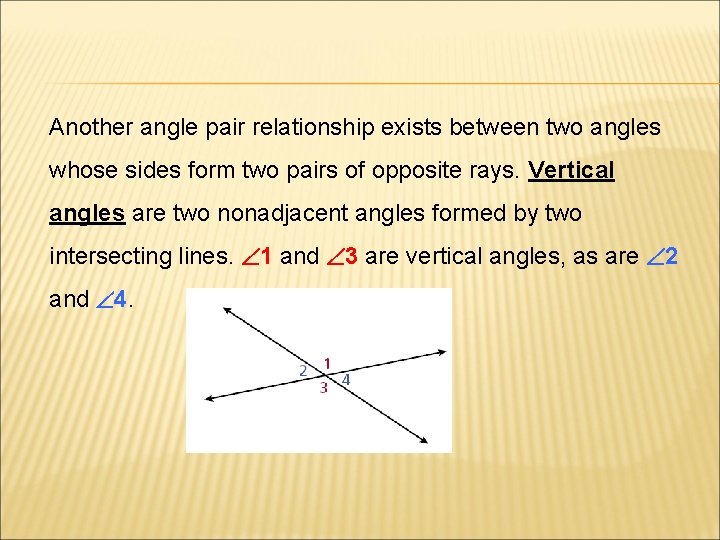
Another angle pair relationship exists between two angles whose sides form two pairs of opposite rays. Vertical angles are two nonadjacent angles formed by two intersecting lines. 1 and 3 are vertical angles, as are 2 and 4.