Section V Sample Size and Power Multiple hypothesis

Section V Sample Size and Power Multiple hypothesis testing

Sample size (n) based on estimation precision-CI width Can plan sample size so that standard errors (SEs) and the corresponding confidence intervals are sufficiently small. (How small? How small do you need it to be? )

Sample size for precision/CIs π = proportion with TB in the population (prevalence) p = proportion with TB in a sample of size n, SE(p) = √[π(1 - π)/n] 95% confidence interval for π: p ± 1. 96(SE) Precision: want to estimate true prevalence (π) within ± 6% Solve for n: 1. 96(SE) = 1. 96 √[π(1 - π)/n] = 0. 06 n = 1. 962 π(1 - π)/(0. 06)2 = 3. 84 π(1 - π)/0. 0036 Can estimate π using the observed p or use maximum at π=0. 5 If π=0. 15, n = 3. 84 (0. 15)(0. 85)/0. 0036 = 136 At π=0. 50, n = 3. 84 (0. 50)/0. 0036 = 267 (worst case) Rule of thumb: For 95% CI for π, conservative n for precision w is n = 1/w 2

Power and Sample size based on hypothesis testing

Hypothesis test decision table Test: Do not reject null Test: Reject null hypothesis No difference in population (Null is true) Actual difference (Null is false) 1 -α (correct) β (Type II error) α (Type I error) 1 -β = power (correct)

Determinants of power Power (1 -β) depends on δ = delta = true difference σ = sigma = true SD or true variation α = alpha = significance criterion n = sample size (Or, n depends on δ, σ, α, 1 -β )

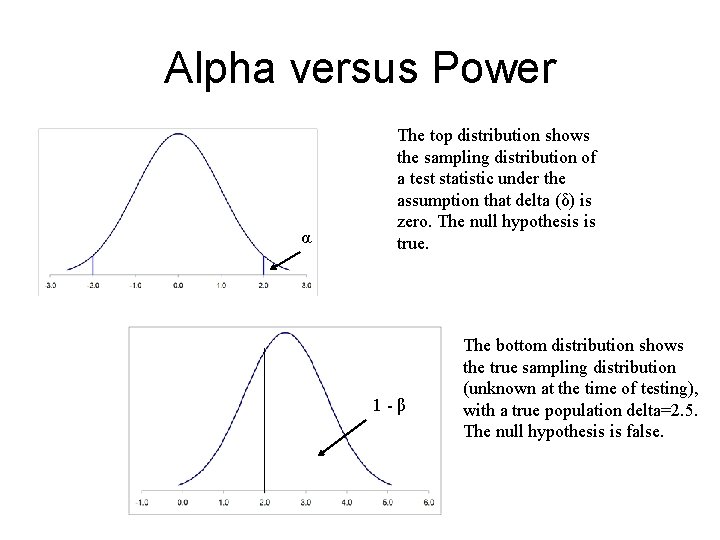
Alpha versus Power • α 1 -β The top distribution shows the sampling distribution of a test statistic under the assumption that delta (δ) is zero. The null hypothesis is true. 1 -β The bottom distribution shows the true sampling distribution (unknown at the time of testing), with a true population delta=2. 5. The null hypothesis is false.

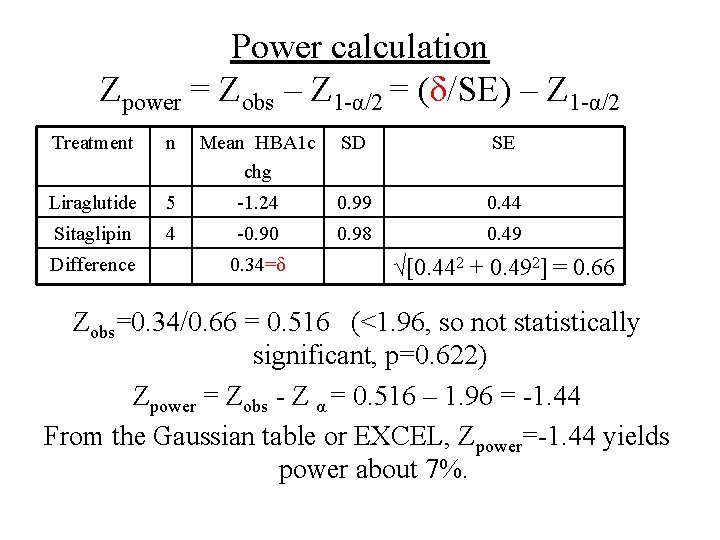
Power calculation Zpower = Zobs – Z 1 -α/2 = (δ/SE) – Z 1 -α/2 Treatment n Mean HBA 1 c chg SD SE Liraglutide 5 -1. 24 0. 99 0. 44 Sitaglipin 4 -0. 90 0. 98 0. 49 Difference 0. 34=δ √[0. 442 + 0. 492] = 0. 66 Zobs=0. 34/0. 66 = 0. 516 (<1. 96, so not statistically significant, p=0. 622) Zpower = Zobs - Z α = 0. 516 – 1. 96 = -1. 44 From the Gaussian table or EXCEL, Zpower=-1. 44 yields power about 7%.

Interpretation of power If test is “statistically” significant (p < α), we have a “positive” or “significant” outcome & accept the false positive probability of α. If test is not statistically significant (p > α) eithere is no relationship (“negative” outcome) or sample size is inadequate (inconclusive outcome). If power is low for a given δ, results are inconclusive, not negative. If power is high, results are affirmatively negative. (But better to quote Confidence interval after the study is published)

Sample size to test difference between 2 means (this is NOT a universal formula) Two independent groups, each with sample size n = 2(Zpower+ Z 1 -α/2)2 (σ/δ)2 Z 0. 975 = 1. 96 and Zpower = 0. 842 (for power of 80%), so n = 2(0. 842 + 1. 96)2 (σ/δ)2 = 15. 7 (σ/δ)2 or n per group approximately ≈ (range/δ)2 (since 15. 7 ≈16, 16(σ/δ)2 = (4σ/δ)2 and the range ≈4σ )

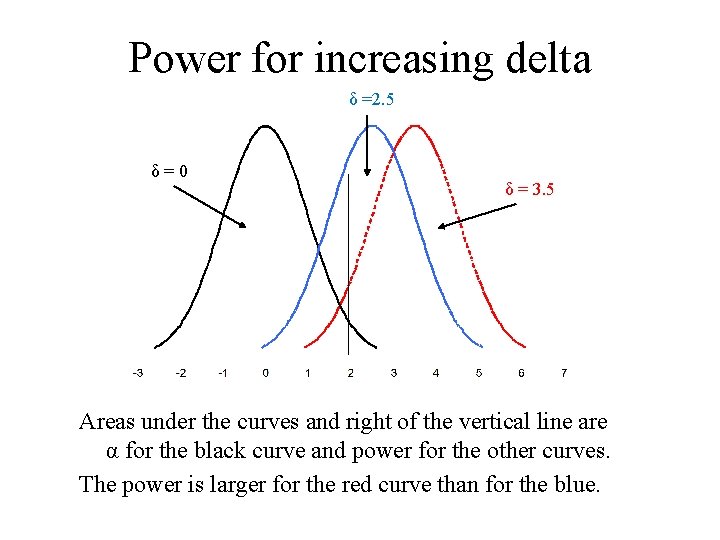
Power for increasing delta δ =2. 5 δ=0 δ = 3. 5 Areas under the curves and right of the vertical line are α for the black curve and power for the other curves. The power is larger for the red curve than for the blue.

Power Summary Power increases as: • • True difference (δ) increases Sample size (n) increases α increases (less strict significance criterion) Patient heterogeneity (σ) decreases Generally, we set α = 0. 05 & power = 1 – β = 0. 80. To determine n, we need to estimate δ and σ. Often we use values of δ/σ for the calculation For time to event outcomes (survival), n also depends on follow up time since “n” is the number of events. The sample size for comparing two survival curves is often computed based on comparing the corresponding two hazards.

Sample Size Checklist Effect size (δ) = smallest clinically important difference (n increases as δ decreases) Variability = patient heterogeneity = group SD (n increases as variability increases) Power = prob of detecting the effect, set at 80% or higher (n increases with power) α level = prob of rejecting when δ=0, usually set at 0. 05, two-sided (n decreases with larger α) ** for time to event (survival) outcomes *** Time of comparison = how long it takes to achieve the effect (n decreases with time) Follow up time = time each patient is followed (n reduced if patients followed longer). In survival “n” is the number who have the outcome. Also consider percentage who will agree to participate patient accrual rate, dropout / loss rate

Sample size for selected δ/σ -2 means (2 means difference= δ, SD=σ, two-sided α=0. 05) δ/σ 70% power 80% power 90% power 0. 10 1, 234 1, 570 2, 102 0. 15 549 698 934 0. 20 309 392 525 0. 25 198 251 336 0. 50 49 63 84 0. 75 22 28 37 1. 00 12 16 21 1. 25 8 10 13 1. 50 5 7 9

Sample size for comparing two proportions 80% power, alpha=0. 05 Smaller of P 1 & P 2 Difference between P 1 and P 2 |P 1 - P 2|=δ 0. 05 0. 10 0. 15 0. 20 0. 05 434 140 71 45 0. 10 685 199 99 62 0. 15 904 250 120 72

Hypothesis testing limitations

Pseudo replication Most variation is between persons, not within person. Two blood samples on n=10 is not a sample size of 20. Observed value = true population mean + between person variation (σp) + within person variation (σe) Example: To estimate the mean 1. Compute a mean for each person using her “m” observations person. 2. Compute the group mean from the “n” person means. SEM = √[σp 2/n + σe 2/nm], usually σe < σp

Statistical vs Medical “significance” (“A difference, in order to be a difference, must make a difference”–Gertrude Stein? ). Average drop in weight (kg) after 3 months Diet Mean Drop I 0. 50 II 10. 0 p 95% CI <0. 001 (0. 45, 0. 55) 0. 16 (-5. 0, 25. 0)

p value limitations (ASA) 1. p values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone ignoring the model. 2. Conclusions should not be based only on whether a pvalue passes a specific threshold. 3. Proper inference requires full reporting & transparency. 4. A p-value does not measure the size of an effect or the importance of a result. 5. A p-value alone does not provide a good measure of evidence regarding a model or hypothesis. 19

R A Fisher on p values Statistical Methods and Scientific Inference, Hafner, New York, ed. 1, 1956 “The concept that the scientific worker can regard himself as an inert item in a vast co-operative concern working according to accepted rules, is encouraged by directing attention away from his duty to form correct scientific conclusions, …and by stressing his supposed duty to mechanically make a succession of automatic “decisions”(ie p< 0. 05). . The idea that this responsibility can be delegated to a giant computer programmed with Decision Functions belongs to a phantasy of circles, rather remote from scientific research”. [pp. 104– 105]

Multiple Hypothesis testing Multiple efficacy endpoints /outcomes Multiple safety endpoints/outcomes Multiple treatment arms and/or doses Multiple interim analyses Multiple patient subgroups Multiple analyses

Exploratory vs confirmatory protein example 750 proteins are compared between two groups – 12 are significant at p < 0. 05 Protein name Atril fib Atherosclerosis p value RAS guanyl-releasing protein 2 Glutathione S-transferase P Selenium-binding protein 1 Nucleosome assembly protein 1 -like 4 Integrin beta; Integrin beta-2 Spectrin alpha chain, non-erythrocytic 1 Pituitary tumor-transforming gene 1 protein-interacting WW domain-binding protein 2 Syntaxin-4 CD 9 antigen ATP synthase-coupling factor 6, mitochondrial Flotillin-1 Aconitate hydratase, mitochondrial Fructose-bisphosphate aldolase C Alpha-adducin 40 S ribosomal protein SA Abl interactor 1 Bone marrow proteoglycan; Eosinophil granule major basic Tubulin alpha-4 A chain … (750 proteins total) 33. 3% 38. 9% 22. 2% 16. 7% 11. 1% 16. 7% 5. 6% 27. 8% 77. 8% 38. 9% 94. 4% 50. 0% 100. 0% 0. 0% 50. 0% 100. 0% 50. 0% 100. 0% 0. 0000 0. 0006 0. 0013 0. 0037 0. 1142 0. 4402 1. 0000

Exploratory vs confirmatory Who killed Tweety Bird?

Did Sylvester do it?

Motivation (class discussion) Tweety Bird is murdered by a cat who left a DNA sample. The particular DNA profile found in the sample is known to occur in one of every one million cats. There is also about a 0. 01% false positive rate for this test. Is the level of evidence (guilt) equal in these two scenarios? 1. Sylvester only is tested and is a match. 2. A DNA database on 100, 000 cats (but not all cats), including Sylvester, is searched and Sylvester is a match, although not necessarily the only match. No prior belief that Sylvester is guilty.

Motivation (class discussion) The “disease score” ranges from 2 (good) to 12 (worst). Scenario A: Due to prior suspicion (prior information), only patients 19 and 47 are measured and both have scores of 12. We report that they are “significantly” ill. Scenario B: The score is measured on 72 patients. Only patients 19 and 47 have scores of 12. We report that they are “significantly” ill.

Is the amount of “evidence” or “belief” that patients 19 and 47 “really” are very ill (have “true” score of 12) the same in both scenarios? The data for patients 19 and 47 are the same in both scenarios. Most would agree that, if both patients were retested (confirmation step), and came out with lower scores, this would decrease the belief that there “true” score is 12. If they came out with 12 again, this would increase the belief that the true score is 12.

Multiple testing “If you torture the data long enough, it will eventually confess” Two different situations for new arthritis treatment compared to aspirin. A. Only pain (0 -10) and swelling (0 -10) are measured. Both are significantly better at p < 0. 05 on the new treatment compared to aspirin. B. Ten different outcomes measured: pain, swelling, activities of daily living, quality of life, sleep, walking, bending, lifting, grinding, climbing. Only the two that are significant are reported after all 10 are evaluated. (fraud? ) Confirmatory studies specify outcomes in advance. Misleading to report only statistically significant results.

How to really lie with stats for fun and profit 1. Bet on the horse after you know who won (Movie -> The “Sting”) 2. Send financial advice after you know how the market did (example in class)

Multiple Testing Out of m (independent) tests, if one declare “significance” if p< 0. 05, below are the number of tests significant by chance alone (FWER), when all null hypotheses are true (assumes independence). # tests=m Probability reject at least one=FWER 1 0. 0500 2 0. 0975 3 0. 1426 4 0. 1855 5 0. 2262 10 0. 4013 20 0. 6415 25 0. 7226 50 0. 9231 m 1 -(0. 95)m

Multiple testing-What to do? Option 1: Use nominal alpha level for significance. Creates too many false positives-bad. Option 2: Use Bonferroni criterion –Declare significance if p < α/m if “m” tests are made. Keeps overall false positive (type I) error ≤ α but has too many false negativesbad. Option 3: Use Holm/Hochberg criterion (or other adjustment criteria) – a compromise

Holm/Hochberg criterion Rule for m (not necessarily independent) significance tests. Keeps overall false positive rate at ≤α for all “m” tests. 1)Sort the “m” p values from lowest to highest. 2)Declare the ith ordered p significant if it is less than α/(m+1 -i). If p > α/(m+1 -i), this & all larger p values are declared non significant. Overall type I error rate (FWER) is ≤ α. (FWER = family wise error rate)

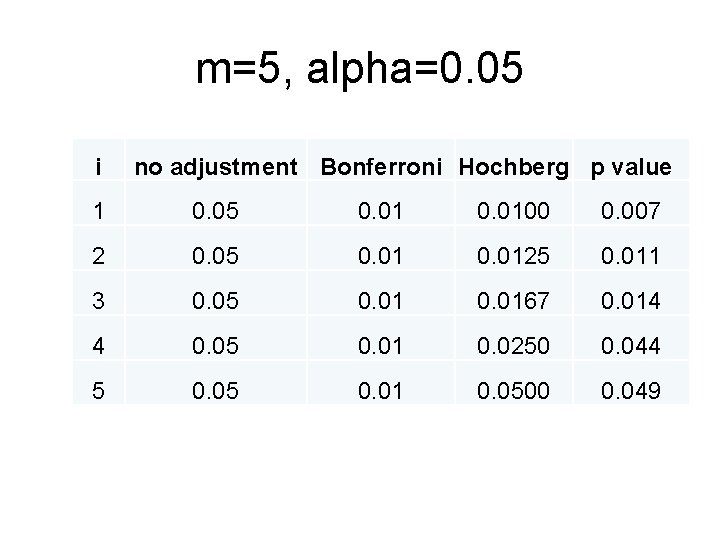
Holm/Hochberg Example for m=5, α=0. 05 i p value α/(6 -i) 0. 05/(6 -i) 1 p 1 -smallest α/5 0. 0100 2 p 2 α/4 0. 0125 3 p 3 α/3 0. 0167 4 p 4 α/2 0. 0250 5 p 5 -largest α 0. 0500 (Bonferroni is p < 0. 05/5 = 0. 01)

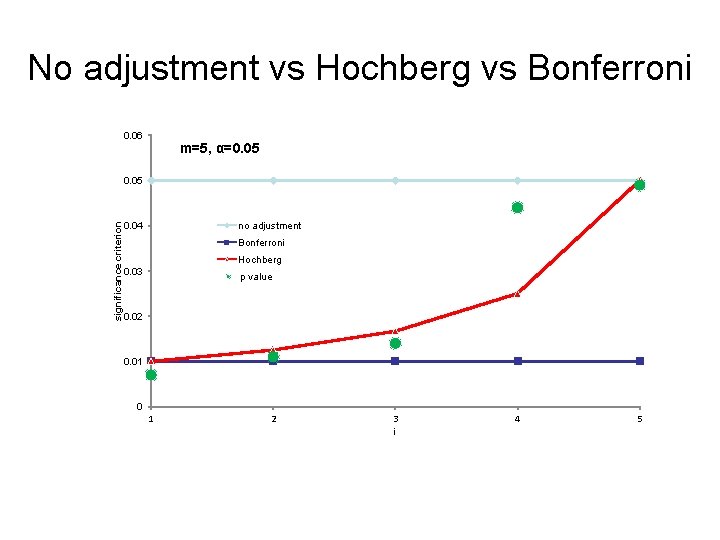
No adjustment vs Hochberg vs Bonferroni m=5, α=0. 05 0. 06 significance criterion 0. 05 no adjustment 0. 04 Bonferroni Hochberg 0. 03 p value 0. 02 0. 01 0 1 2 3 i 4 5

m=5, alpha=0. 05 i no adjustment Bonferroni Hochberg p value 1 0. 05 0. 0100 0. 007 2 0. 05 0. 0125 0. 011 3 0. 05 0. 0167 0. 014 4 0. 05 0. 01 0. 0250 0. 044 5 0. 01 0. 0500 0. 049

FWER vs FDR If a “family” of “m” hypothesis tests are carried out, the family wise error rate (FWER) is the chance of any “false positive” type I error assuming that the null is true for all tests (not looking at test result). Rather than control the FWER, it may be preferable to control the number of “positive” tests (not all tests) that are false positives. This is called controlling the false discovery rate (FDR), a less stringent criterion. For FDR, the ith ordered p value must be less than (i/m)α which is larger than α/(m+1 -i) for FWER.

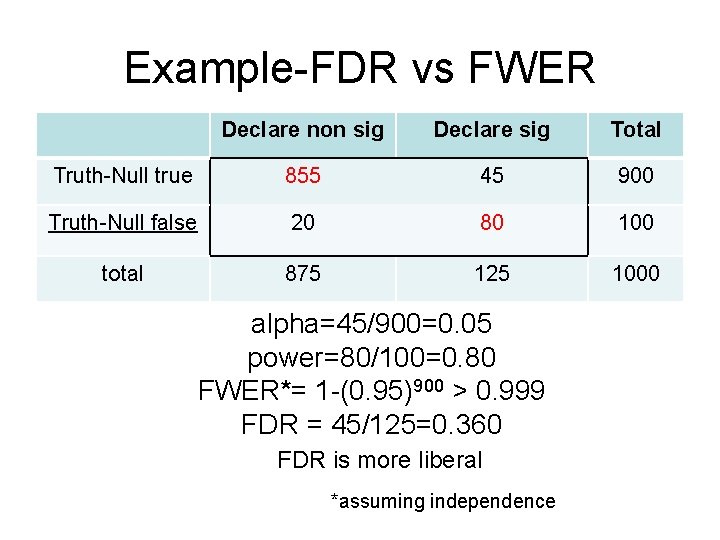
FDR vs FWER errors committed when testing “m” null hypotheses Declare non sig Declare sig Total Truth-Null true U V m 0 Truth-Null false T S m-m 0 total m-R R m FWER= Prob V ≥ 1 = 1 - Prob(V=0) FDR = V/R (average V/R) FDR is more liberal

Example-FDR vs FWER Declare non sig Declare sig Total Truth-Null true 855 45 900 Truth-Null false 20 80 100 total 875 125 1000 alpha=45/900=0. 05 power=80/100=0. 80 FWER*= 1 -(0. 95)900 > 0. 999 FDR = 45/125=0. 360 FDR is more liberal *assuming independence

FWER vs FDR significance criteria m=5 hypothesis, 5 p values α=0. 05 p value FDR criteria FEWR criteria p 1 -smallest (1/5) α=0. 01 α/5=0. 01 p 2 (2/5) α=0. 02 α/4=0. 0125 p 3 (3/5) α=0. 03 α/3=0. 0167 p 4 (4/5) α=0. 04 α/2=0. 025 p 5 -largest α=0. 05

FDR – q values When controlling for the FDR at rate α, the “m” p values must be less than (i/m)α in order to be significant (i=1, 2, 3, …m). Therefore, some will report “q values”, defined as q value = (p value) (m/i) Instead of p values. when i=1, q value = m p value when i=m, q value = p value

Courtesy of Graph Pad

Multiple testing & primary outcomes As “m’, the number of outcomes, increases, individual αi for each outcome must be smaller so n must be larger if overall α is to stay constant (ie at α=0. 05). But not all outcomes are equally important. Designate important outcomes “primary” & the rest secondary so ‘m’ is only the number of primary outcomes. Assumes less concern if there is a false positive finding among secondary outcomes. Must designate primary vs secondary outcomes in advance, before study results are known. It is not fair to declare which outcomes are primary and which are secondary based on their p values.

Statistical Analysis Plan Statistical models and methods to answer study questions Conclusions = data + models (assumptions) Each specific aim needs a stat analysis section. Sample size and power follows the analysis plan. Outline: • Outcomes: denote primary & secondary • Primary predictors or comparison groups • Covariates/confounders/effect modifiers • Methods for missing data, dropouts • Interim analyses (for efficacy, for safety)

Common Methods Univariate analysis Continuous outcome: Means, SDs, medians Time to event: Survival curves Discrete: Proportions Multivariate analysis Continuous outcome: Linear regression, correlation Positive integers: Poisson regression Binary (yes/no): Logistic regression Time to event: Proportional hazard regression ANOVA and t-test are special cases of linear regression