Section 9 3 Arcs and Central Angles Central

Section 9 -3 Arcs and Central Angles

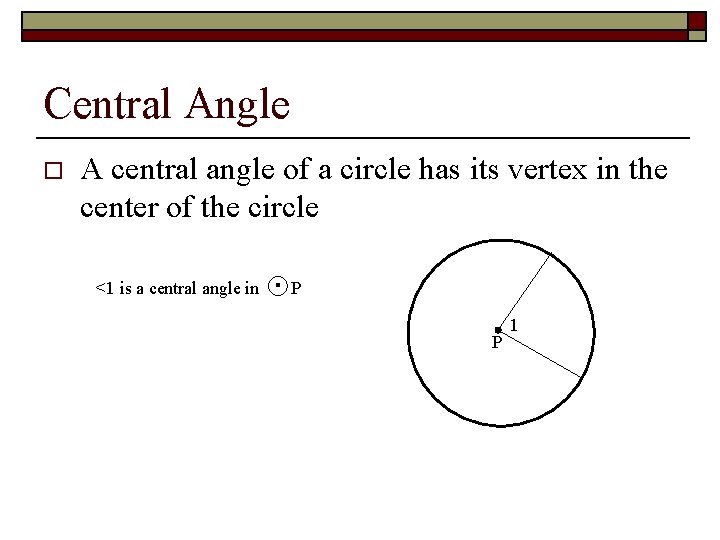
Central Angle o A central angle of a circle has its vertex in the center of the circle <1 is a central angle in . P P 1

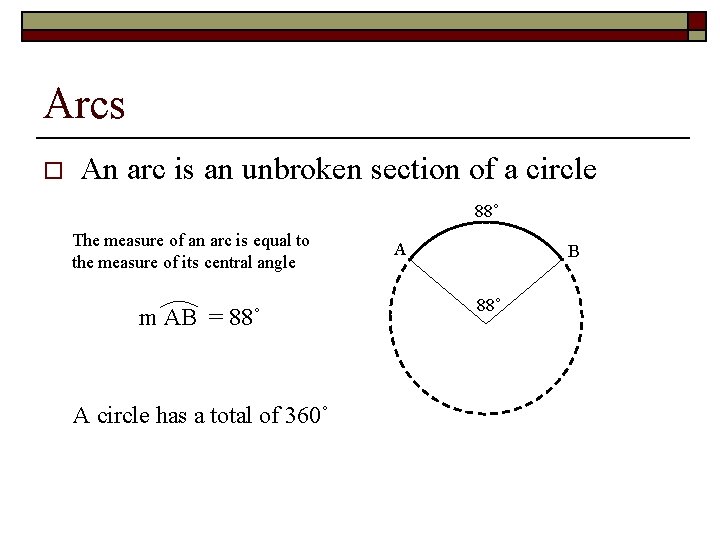
Arcs o An arc is an unbroken section of a circle 88˚ The measure of an arc is equal to the measure of its central angle m AB = 88˚ A circle has a total of 360˚ A B 88˚

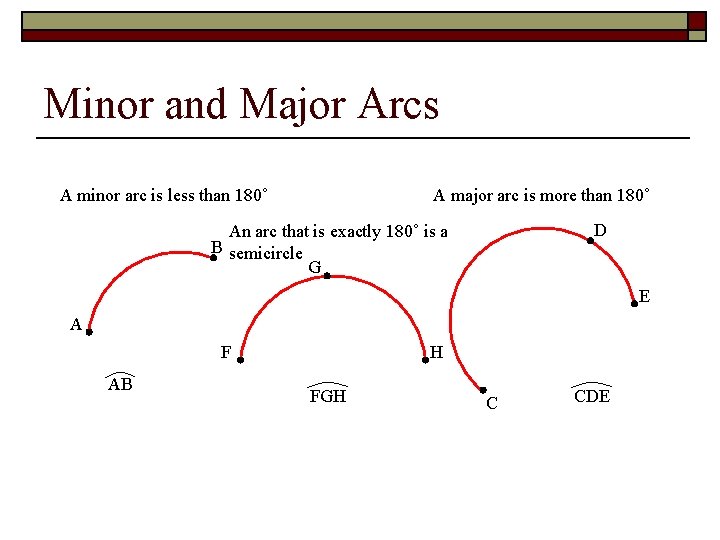
Minor and Major Arcs A minor arc is less than 180˚ A major arc is more than 180˚ D An arc that is exactly 180˚ is a B semicircle G E A F AB H FGH C CDE

It’s like… A circle that has been cut in half.

Example 1 C If CA is a diameter of circle O: Name: 1. Two minor arcs 2. Two major arcs O R 3. Two semicircles 4. An acute central angle 5. Two arcs with the same measure A S

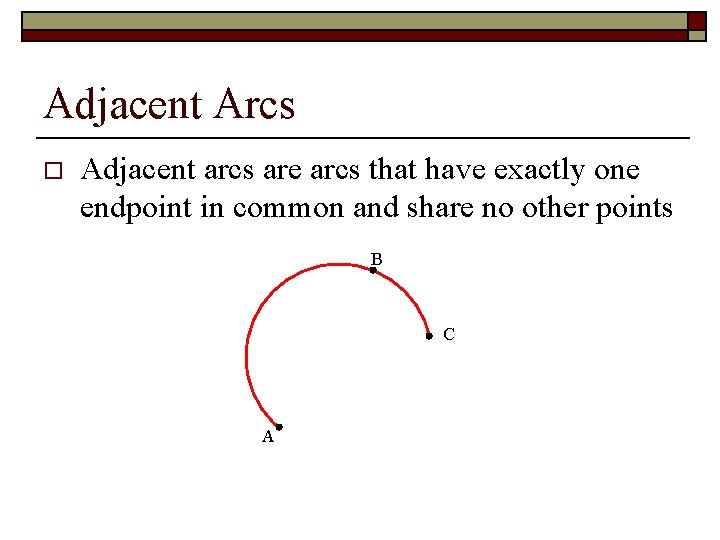
Adjacent Arcs o Adjacent arcs are arcs that have exactly one endpoint in common and share no other points B C A

Arc Addition Postulate (postulate 16) o The measure of the arc formed by two adjacent arcs is the sum of the measures of these arcs. B m AB + m BC = m ABC 64˚ 140˚ C A Example: m ABC = 204˚

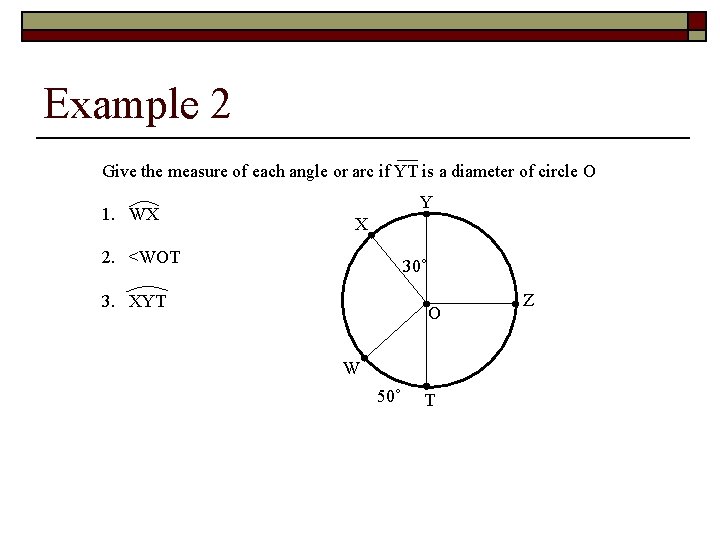
Example 2 Give the measure of each angle or arc if YT is a diameter of circle O 1. WX Y X 2. <WOT 30˚ 3. XYT O W 50˚ T Z

Congruent Arcs o Two arcs are congruent if they have the same measure, and if they lie on the same circle or two congruent circles. C B 67˚ O D 67˚ A

Congruent Arcs o Two arcs are congruent if they have the same measure, and if they lie on the same circle or two congruent circles. P B F 8 cm 75˚ I O 75˚ 8 cm D

Theorem 9 -3 o In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. P Conclusion: m<1 = m<2 1 F B T 8 cm 75˚ 2 8 cm A 75˚ I

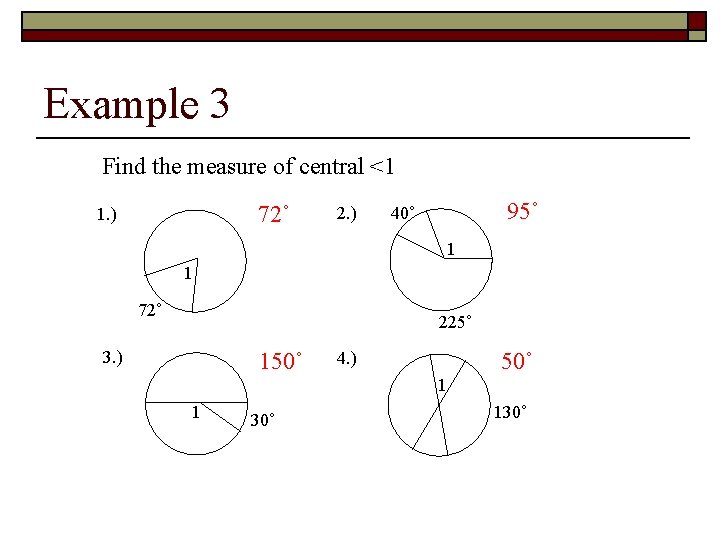
Example 3 Find the measure of central <1 72˚ 1. ) 2. ) 95˚ 40˚ 1 1 72˚ 225˚ 3. ) 150˚ 4. ) 1 1 30˚ 130˚

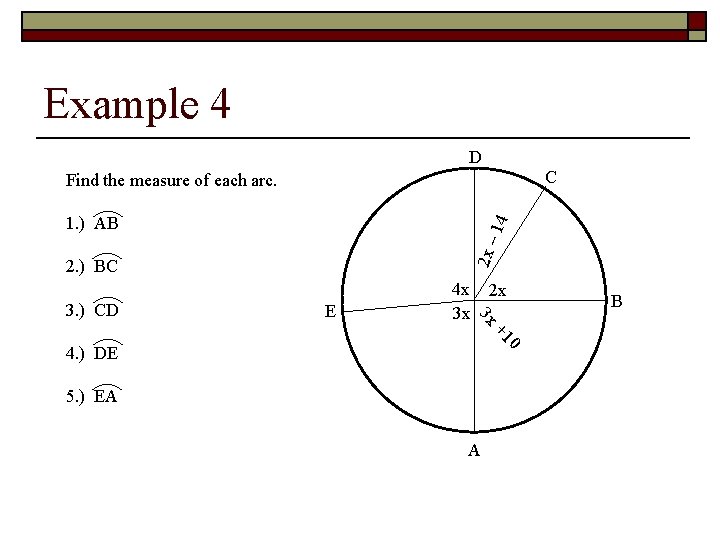
Example 4 D C Find the measure of each arc. 2 x – 14 1. ) AB 2. ) BC E 2 x 3 x 3. ) CD 4 x 3 x +1 0 4. ) DE 5. ) EA A B

Or is it? The End