Section 9 3 Absolute Value Equations and Inequalities

Section 9. 3 Absolute – Value Equations and Inequalities

Absolute Value Definition Absolute Value The absolute value of x, denoted as | x |. is defined as |x|= x or -x When x is nonnegative, the absolute value of x is x When x is negative, the absolute value of x is -x

Example Simplify | -5 | Simplify | 56 | Simplify | -3. 6 | Simplify |14 – 3 | Simplify | 26 – 45 | Simplify | 123 – 35 – 89 | Simplify | 349 + 12 – 876|

Example Rewrite without an absolute value | 2 x | Rewrite without an absolute value | x – 2 | Rewrite without an absolute value | 2 x + 5 |

Absolute Value Equation Steps to solve an absolute value equation 1) Isolate the absolute value 2) Break the absolute value into the two equations, the positive and negative with the conjunction word OR between them 3) Solve each equation independently 4) Check all solutions. 5) Possible Answers Finite Solutions No Solution Infinite Solution

EXAMPLE Solve the equation 2 |x – 4| = 16 2 | x – 4 | = 16 | x – 4| = 8 (x – 4) = 8 OR x– 4=8 x = 12 2 |12 – 4| = 16 2 |-4 – 4| = 16 2|-8| = 16 2(8)=16 OR -x + 4 = 8 OR OR -(x – 4) = 8 -x = 4 x = -4 2|8| = 16 2(8)=16 16=16

EXAMPLE Solve the equation | y + 3| + 5 = 12

EXAMPLE Solve the equation | y + 3| + 5 = 2

EXAMPLE Solve the equation 2| 3 y - 1| - 8 = 2

EXAMPLE Solve the equation 5 - 2| y - 1| = 3

EXAMPLE Solve the equation 5 - 2| 3 y - 1| = 13

EXAMPLE Solve the equation 2| 3 y - 1| - 8 = 2

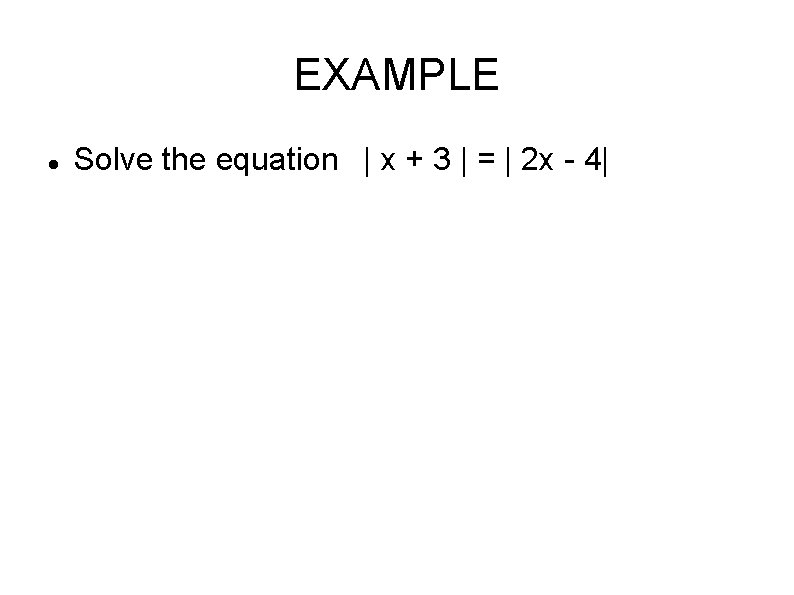
EXAMPLE Solve the equation | x + 3 | = | 2 x - 4|

Absolute Values Inequalities Steps Isolate the absolute value. Break the absolute value into two inequalities If the isolated inequality was < or ≤ separate with AND. If the isolated inequality was > or ≥ separate with OR. Solve each inequality separately. Try to put answers together. Determine how many answers. Write answer in the specified form Graphing Notation Interval Notation

EXAMPLE Solve the absolute value inequality and write answer in set builder notation: 2|x – 3| < 2 2|x-3|<2 |x– 3|<1 (x – 3) < 1 x– 3<1 AND -x + 3 < 1 x<4 AND -x < -2 x<4 AND x>2 { x | 2 < x < 4} AND -(x – 3) < 1

EXAMPLE Solve the absolute value inequality and write answer in interval notation: -2|x – 3| < 2 -2 | x - 3 | < 2 | x – 3 | > -1 (x – 3) > -1 OR -(x – 3) > -1 X – 3 > -1 OR -x + 3 > -1 X>2 OR -x > -4 X>2 OR x<4 (-∞, ∞)

EXAMPLE Solve the absolute value inequality and write answer in set builder notation: 4 + |2 x + 1| ≥ -8

EXAMPLE Solve the absolute value inequality and write answer in interval notation: 4 - 2 |2 x + 1| ≥ -8

EXAMPLE Solve the absolute value inequality and write answer in graphing notation: - 3 |2 y +- 1| - 1 ≤ +8

HOMEWORK 9. 3 # 15, 22, 23, 30, 37, 40, 47, 54, 57, 66, 73, 84