Section 9 2 Significance Test for a Mean

Section 9. 2 Significance Test for a Mean

Homework Activity 9. 2 a, page 581 • Due tomorrow • Use complete sentences to support your answers. • For each question, be sure to explain why you made the choice you did.

Test Statistic When we tested for the mean of a sampling distribution, we used: Recall, μ 0 is hypothesized population mean

Population Mean To test H 0: , we need a test statistic. However, we do not know so what do we do?

Test Statistic We substitute s for and t for z.

Test Statistic We substitute s for and t for z. The test statistic becomes:

Test Statistic The weights of newly minted U. S. pennies are approximately normally distributed and are targeted to have a mean weight of 3. 11 g. The random sample of nine pennies has a mean weight of 3. 16 g with a standard deviation of 0. 065. What is the value of a test statistic for a test to determine whether the mean has moved away from the target mean?

Test Statistic

Test Statistic t 2. 31

t-Distributions Suppose you draw random samples of size n from a normally distributed population with mean μ and unknown standard deviation σ.

t-Distributions Suppose you draw random samples of size n from a normally distributed population with mean and unknown standard deviation. The distribution of the values of: is called a t-distribution. There is a different t-distribution for each degree of freedom.

t-Distributions A t-distribution is: • mound-shaped • with mean 0 and • a spread that depends on the value of the degrees of freedom (df).

t-Distributions A t-distribution is: • mound-shaped • with mean 0 and • a spread that depends on the value of the degrees of freedom (df). The greater the df, the smaller the spread.

t-Distributions A t-distribution is mound-shaped, with mean 0 and a spread that depends on the value of df. The greater the df, the smaller the spread. The spread of any t-distribution is greater than that of the standard normal distribution.

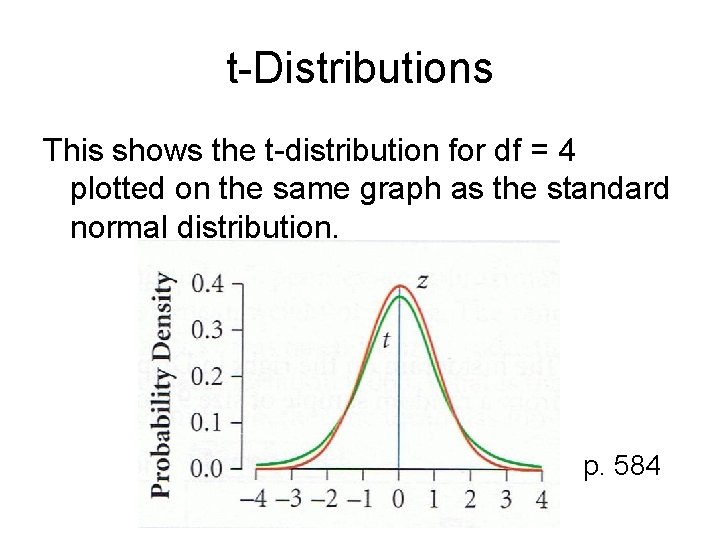
t-Distributions This shows the t-distribution for df = 4 plotted on the same graph as the standard normal distribution. p. 584

t-Distributions 1) For the degrees of freedom to increase, what has to happen?

t-Distributions 1) For the degrees of freedom to increase, what has to happen? Sample size must increase as df = n -1.

t-Distributions 1) For the degrees of freedom to increase, what has to happen? Sample size must increase as df = n -1. 2) As sample size, n, increases what happens to s?

t-Distributions 1) For the degrees of freedom to increase, what has to happen? Sample size must increase as df = n -1. 2) As sample size, n, increases what happens to s? s

t-Distributions 1) For the degrees of freedom to increase, what has to happen? Sample size must increase as df = n -1. 2) As sample size, n, increases what happens to s? s 3) As s , what happens to the t-distribution?

t-Distributions 1) For the degrees of freedom to increase, what has to happen? Sample size must increase as df = n -1. 2) As sample size, n, increases what happens to s? s 3) As s , what happens to the t-distribution? t-distribution more closely approximates a standard normal distribution

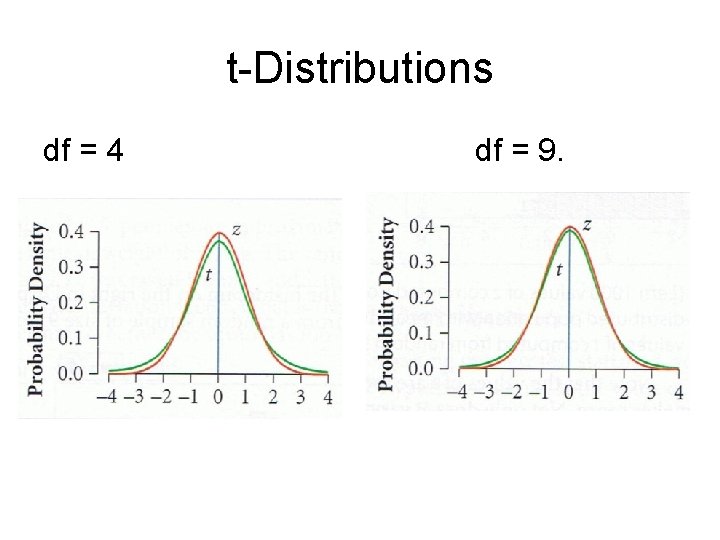
t-Distributions Therefore, as the degrees of freedom increase, the t-distribution more closely approximates a standard normal distribution

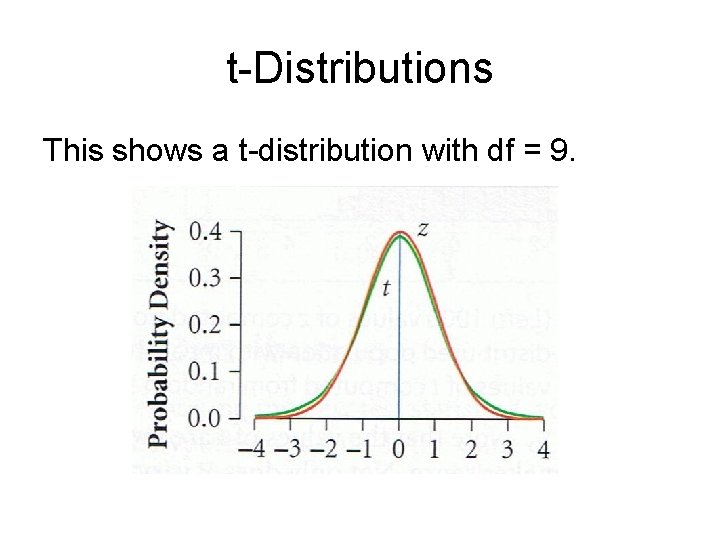
t-Distributions This shows a t-distribution with df = 9.

t-Distributions df = 4 df = 9.

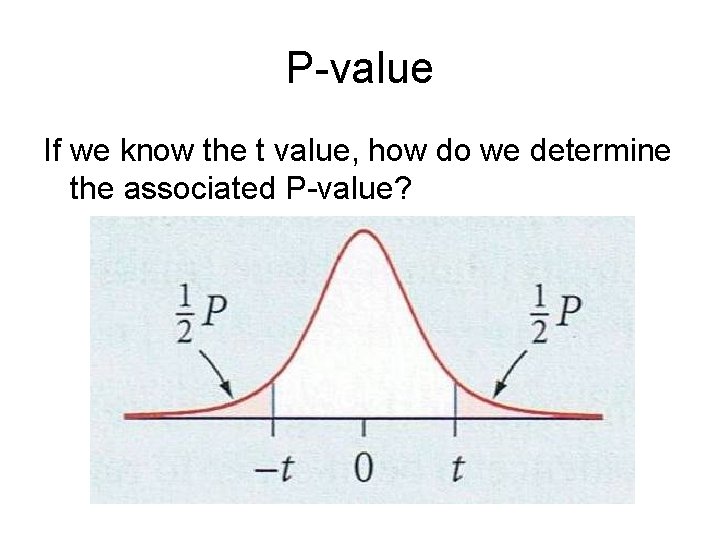
P-value If we know the t value, how do we determine the associated P-value?

P-value If we know the t value, how do we determine the associated P-value?

P-value Recall, if we had a z-distribution we would use _____. Since we have a t-distribution we need to use _______?

P-value Recall, if we had a z-distribution we would use normalcdf. Since we have a t-distribution we need to use _______?

P-value Recall, if we had a z-distribution we would use normalcdf. Since we have a t-distribution we need to use tcdf. 2 nd, DISTR, 6: tcdf

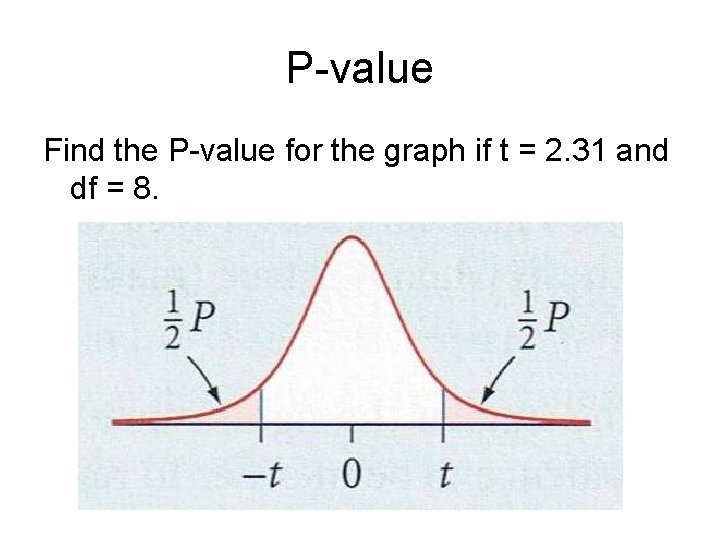
P-value Find the P-value for the graph if t = 2. 31 and df = 8.

P-value Syntax: tcdf(lower bound, upper bound, df) Recall: There is a different t-distribution for each degree of freedom so we have to specify df here

P-value Syntax: tcdf(lower bound, upper bound, df) P-value = 2[ tcdf (-1 EE 99, - 2. 31, 8)] = 2(. 0248445422) = 0. 0496890845

Components of a Significance Test for a Mean 4 components:

Components of a Significance Test for a Mean 4 components: 1) Name the test and check conditions

Components of a Significance Test for a Mean 4 components: 1) Name the test and check conditions 2) State hypotheses

Components of a Significance Test for a Mean 4 components: 1) Name the test and check conditions 2) State hypotheses 3) Compute test statistic, find Pvalue, and draw a sketch

Components of a Significance Test for a Mean 4 components: 1) Name the test and check conditions 2) State hypotheses 3) Compute test statistic, find P-value, and draw a sketch 4) Write conclusion linked to computations and in context.

Name Test Two-sided significance test for a mean or One-sided significance test for a mean

Check Conditions 1) Randomness

Check Conditions 1) Randomness – Survey: random sample

Check Conditions 1) Randomness – Survey: random sample – Experiment: randomly assigned treatments

Check Conditions 2) Normality

Check Conditions 2) Normality Sample must look like it’s reasonable to assume that the sample came from a normally distributed population or Sample size must be large enough that the sampling distribution of the sample mean is approximately normal (will discuss in Section 9. 3)

Check Conditions 3) Population size

Check Conditions 3) Population size Survey: population size is at least 10 times as large as the sample

Check Conditions 3) Population size Survey: population size is at least 10 times as large as the sample Experiment: not applicable

State Hypotheses

State Hypotheses Null hypothesis is that the population mean, μ, has a particular value μo. Define μ in context. H o:

State Hypotheses Null hypothesis is that the population mean, μ, has a particular value μo. Define μ in context. H o: Example: Ho: μ = 3. 85, where μ is the mean GPA for acceptance at Harvard

State Hypotheses Alternative hypothesis is one of these: H a: < H a: > Use specific value for

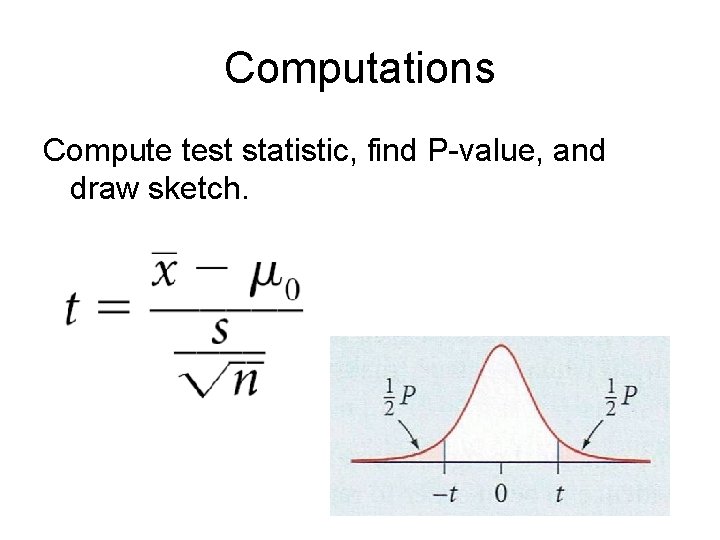
Computations Compute test statistic, find P-value, and draw sketch.

Computations by Calculator STAT

Computations by Calculator STAT

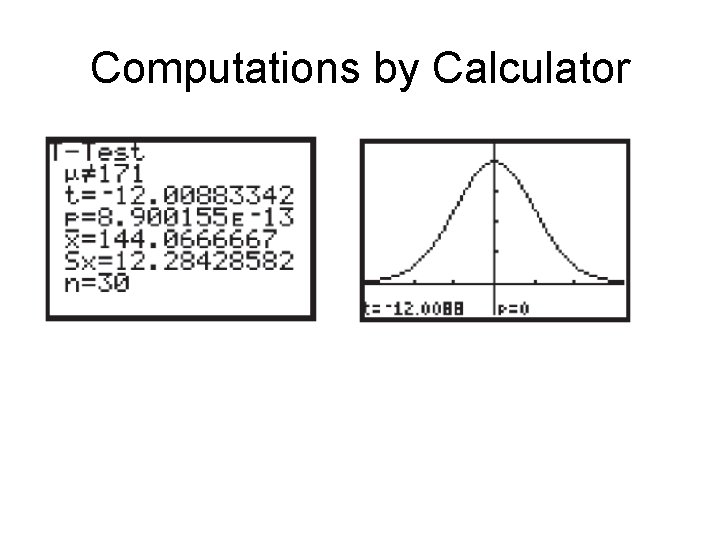
Computations by Calculator

Conclusion Write conclusion linked to your computations and in the context of the problem. Remember, if you are not given a level of significance, you can assume = 0. 05

Page 596, P 10 Find the test statistic, t, and the P-value.

T-test Inpt: Data Stats μ 0: 72 List: L 1 Freq: 1 μ: ≠ μ 0 < μo > μo Calculate

T-test μ ≠ 72 t = - 2. 931419509 p =. 0262386012 x = 70. 14285714 Sx = 1. 67616342 n=7 t ≈ ± 2. 9314

Page 596, P 10

Page 597, P 14

Page 597, P 14 The test statistic, t, is approx. ± 2. 9315 P-value = 2[ tcdf (-1 EE 99, - 2. 9315, 6)] = 0. 0262358556

Page 597, P 14 The test statistic, t, is approx. -2. 9315 P-value = 2[ tcdf (-1 EE 99, - 2. 9315, 6)] = 0. 0262358556 If the mean temperature at the desk is actually 720, the probability that temperatures taken on seven randomly selected days would give a result as extreme or more extreme than 2. 9315 is about 0. 0262

Page 597, P 16

Page 597, P 16 a) Ho: μ = 720, where μ is the mean temperature at my desk

Page 597, P 16 a) Ho: μ = 720, where μ is the mean temperature at my desk Ha: μ ≠ 720.

Page 597, P 16 b) P-value is about 0. 0262 10% level: reject Ho because P-value of about 0. 0262 is less than = 0. 10 5% level: 1% level:

Page 597, P 16 b) P-value is about 0. 0262 10% level: reject Ho because P-value of about 0. 0262 is less than = 0. 10 5% level: reject Ho because P-value of about 0. 0262 is less than = 0. 05 1% level:

Page 597, P 16 b) P-value is about 0. 0262 10% level: reject Ho because P-value of about 0. 0262 is less than = 0. 10 5% level: reject Ho because P-value of about 0. 0262 is less than = 0. 05 1% level: do not reject Ho because P-value of about 0. 0262 is greater than = 0. 01

Questions?