Section 8 7 Word Problems Involving Radicals Direct

Section 8. 7 Word Problems Involving Radicals: Direct and Inverse Variation Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc.

Variation A variation is an equation that relates one variable to another variable. If a variable y varies directly as x, then y = kx, where k is the constant of variation. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 2

Solving a Direct Variation Problem Write the direct variation equation. 2. Solve for the constant k by substituting in known values. 3. Replace k in the direct variation equation by the value obtained in step 2. 4. Solve for the desired value. 1. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 3

Example If y varies directly as x, and y = 16 when x = 7, find the value of y when x = 30. Step 1: y = kx Step 2: To find k, substitute y = 16 and x = 7. Step 3: We now write the variation equation with k replaced by 16/7. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 4

Example (cont) If y varies directly as x, and y = 16 when x = 7, find the value of y when x = 30. Step 4: Replace x by 30 and find the value of y. Therefore, y is approximately 68. 6 when x = 30. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 5

Sample Direct Variation Situations Verbal Description y varies directly as x Variation Equation y = kx b varies directly as the square of c b = kc 2 l varies directly as the cube of m l = km 3 V varies directly as the square root of h Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 6

Example There are 14 blonde-haired students in a statistics class with 45 students. The number of total students in the class varies directly with the number of blonde-haired students. Approximately how many students will there be in a statistics class if there are 25 blonde-haired students? Step 1: Let S = the total number of students. Let b = the number of blonde-haired students. S = kb Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 7

Example (cont) There are 14 blonde-haired students in a statistics class with 45 students. The number of total students in the class varies directly with the number of blondehaired students. Approximately how many students will there be in a statistics class if there are 25 blonde-haired students? Step 2: To find k, substitute S = 45 and b = 14. Step 3: Write the variation equation. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 8

Example (cont) There are 14 blonde-haired students in a statistics class with 45 students. The number of total students in the class varies directly with the number of blondehaired students. Approximately how many students will there be in a statistics class if there are 25 blonde-haired students? Step 4: Replace b by 25 and find the value of S. There will be approximately 80 students in the class. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 9

Solving an Inverse Variation Problem Write the inverse variation equation. 2. Solve for the constant k by substituting in known values. 3. Replace k in the inverse variation equation by the value obtained in step 2. 4. Solve for the desired value. 1. If a variable y varies inversely as x, then k is the constant of variation. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. where 10

Example If y varies inversely as x, and y = 24 when x = 10, find the value of y when x = 36. Step 1: Step 2: To find k, substitute y = 24 and x = 10. Step 3: Write the variation equation. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 11

Example (cont) If y varies inversely as x, and y = 24 when x = 10, find the value of y when x = 36. Step 4: Replace x by 36 and find the value of y. Therefore, y is approximately 6. 7 when x = 36. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 12

Sample Inverse Variation Situations Verbal Description y varies inversely as x Variation Equation b varies inversely as the square of c l varies inversely as the cube of m d varies inversely as the square root of t Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 13

Example Sally spends 1. 5 hours watching television and 8 hours studying each week. If the amount of time spent watching TV varies inversely with the amount of time spent studying, find the amount of time Sally will spend watching TV if she studies 14 hours a week. Step 1: Let T = the number of hours spent watching television. Let s = the number of hours spent studying. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 14

Example (cont) Sally spends 1. 5 hours watching television and 8 hours studying each week. If the amount of time spent watching TV varies inversely with the amount of time spent studying, find the amount of time Sally will spend watching TV if she studies 14 hours a week. Step 2: To find k, substitute T = 1. 5 and s = 8. Step 3: Write the variation equation. Step 4: Replace s by 14 and find the value of T. Sally will spend approximately 0. 86 hours (or 52 minutes) watching TV. Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 15
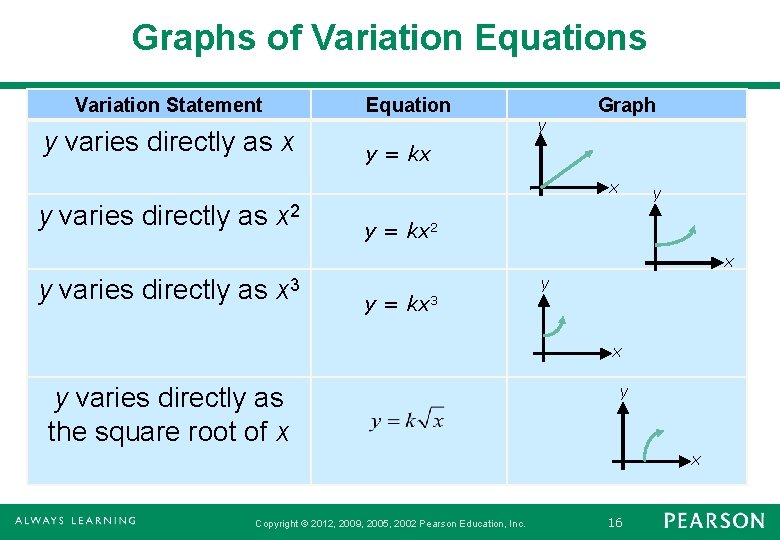
Graphs of Variation Equations Variation Statement y varies directly as x Equation y Graph y = kx x y varies directly as x 2 y y = kx 2 x y varies directly as x 3 y = kx 3 y x y varies directly as the square root of x y x Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 16
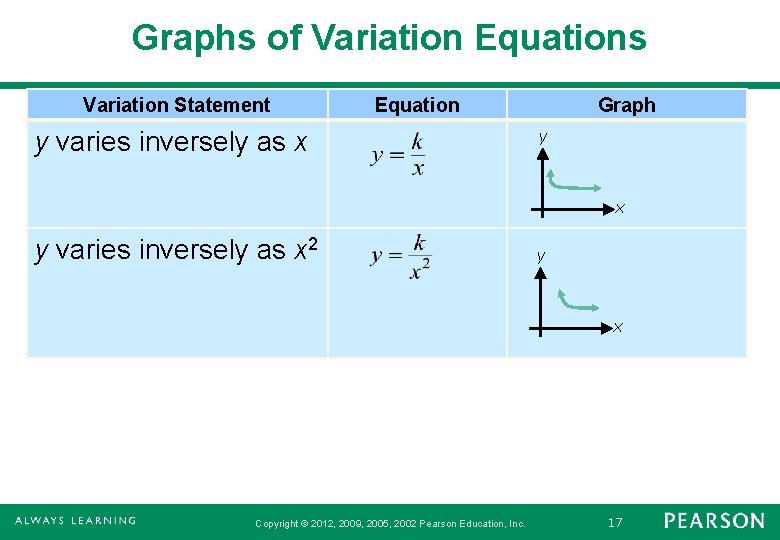
Graphs of Variation Equations Variation Statement Equation y varies inversely as x Graph y x y varies inversely as x 2 y x Copyright © 2012, 2009, 2005, 2002 Pearson Education, Inc. 17
- Slides: 17