Section 8 6 Vector Operations Copyright 2013 2009

Objectives Perform calculations with vectors in component form. Express a vector as a linear

Position Vectors The vector v whose initial point is at the origin and whose

Horizontal and Vertical Components The coordinate a is the scalar horizontal component of the

Component Form a Vector The component form of

Length of a Vector The length, or magnitude, of a vector Is given by

Equivalent Vectors Two vectors are equivalent if they have the same magnitude and the

Operations on Vectors For a real number k and a vector the scalar product

Vector Addition and Subtraction It is interesting to compare the sum of two vectors

Example Do the following calculations where Solution:

Unit Vectors A vector of magnitude, or length, 1 is called a unit vector.

Example Find a unit vector that has the same direction as the vector Solution:

Linear Combination of Unit Vectors The unit vectors parallel to the x- and y-axes

Direction Angles The terminal point P of a unit vector in standard position is

Vectors and Forces If two forces F 1 and F 2 act on an

Example An airplane travels on a bearing of 100º at an airspeed of 190

Example (cont) Bearing of airspeed Direction angle of Bearing of wind Direction angle of

Example (cont) Let be the direction angle of v. Thus the course of the

Dot Product The dot product of two vectors Note that u 1 v 1

Angle Between Two Vectors If is the angle between two nonzero vectors u and

Example Find the angle between Solution: Find u • v, |u| and |v|.

Forces in Equilibrium When several forces act through the same point on an object,

Example A 350 -lb block is suspended by two cables. At point A, there

Example (cont) Substitute R, S, and W into So we have two equations:

Example (cont) Solve equation 1 for |R|. Substitute this expression into equation 2. Solving

Slides: 30

Download presentation

Objectives Perform calculations with vectors in component form. Express a vector as a linear combination of unit vectors. Express a vector in terms of its magnitude and its direction. · Find the angle between two vectors using the dot product. · Solve applied problems involving forces in equilibrium. · · ·

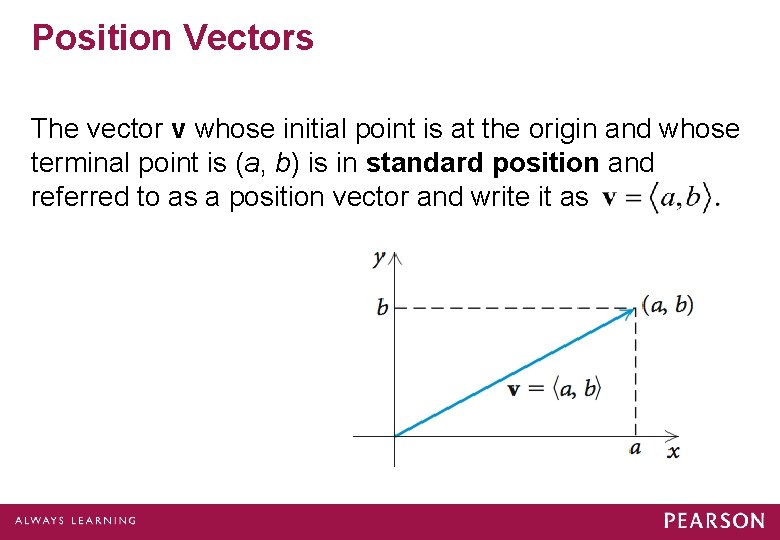
Position Vectors The vector v whose initial point is at the origin and whose terminal point is (a, b) is in standard position and referred to as a position vector and write it as

Horizontal and Vertical Components The coordinate a is the scalar horizontal component of the vector, and the coordinate b is the scalar vertical component of the vector. By scalar, we mean a numerical quantity rather than a vector quantity. Thus, is considered to be the component form of v. Note that a and b are not vectors and should not be confused with the vector component definition.

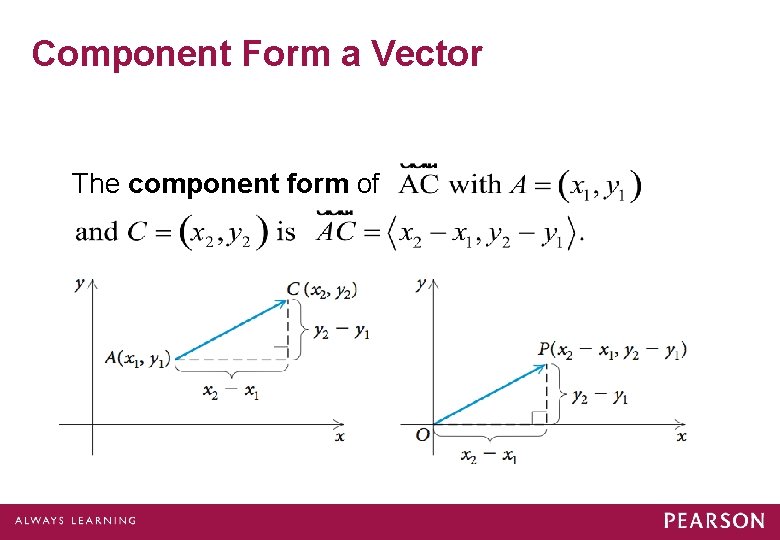
Component Form a Vector The component form of

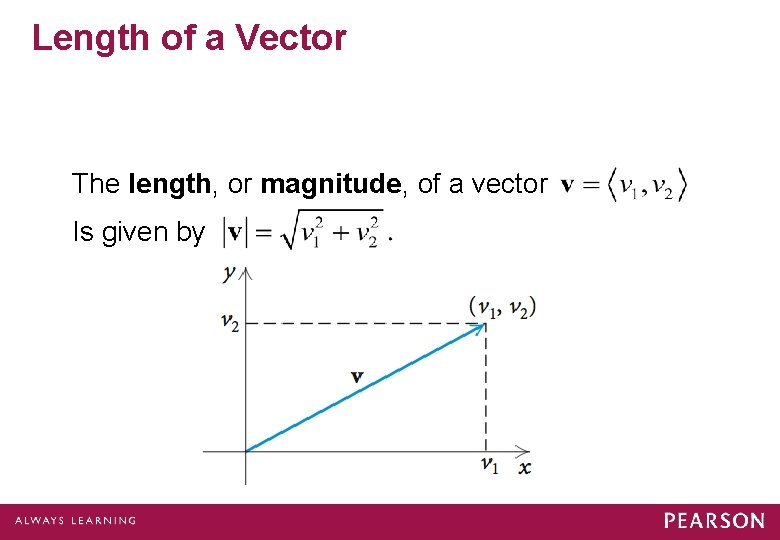
Length of a Vector The length, or magnitude, of a vector Is given by

Equivalent Vectors Two vectors are equivalent if they have the same magnitude and the same direction.

Operations on Vectors For a real number k and a vector the scalar product of k and a v is The vector kv is a scalar multiple of the vector v.

Vector Addition

Vector Subtraction

Vector Addition and Subtraction It is interesting to compare the sum of two vectors with the difference of the same two vectors in the same parallelogram. The vectors u + v and u – v are the diagonals of the parallelogram.

Example Do the following calculations where Solution:

Example (cont)

Unit Vectors A vector of magnitude, or length, 1 is called a unit vector. If v is a vector and v ≠ O, then is a unit vector in the direction of v.

Example Find a unit vector that has the same direction as the vector Solution: Find the length of w. Use the formula for a unit vector.

Linear Combination of Unit Vectors The unit vectors parallel to the x- and y-axes are particularly useful and defined to be Any vector can be expressed as a linear combination of unit vectors i and j.

Direction Angles The terminal point P of a unit vector in standard position is a point on the unit circle denoted by (cos , sin ). Thus the unit vector can be expressed in component form, or as a linear combination of the unit vectors i and j, where the components of u are functions of the direction angle measured counterclockwise from the x-axis to the vector.

Vectors and Forces If two forces F 1 and F 2 act on an object, the combined effect is the sum, or resultant, F 1 + F 2 of the separate forces.

Example An airplane travels on a bearing of 100º at an airspeed of 190 km/h while a wind is blowing 48 km/h from 220º. Find the ground speed of the airplane and the direction of its track, or course, over the ground. Solution: Make a drawing.

Example (cont) Bearing of airspeed Direction angle of Bearing of wind Direction angle of The magnitudes of are 190 and 48, respectively. A

Example (cont) Thus, Ground speed

Example (cont) Let be the direction angle of v. Thus the course of the airplane (the direction from north) is 90º – 1º, or 89º.

Dot Product The dot product of two vectors Note that u 1 v 1 + u 2 v 2 is a scalar, not a vector.

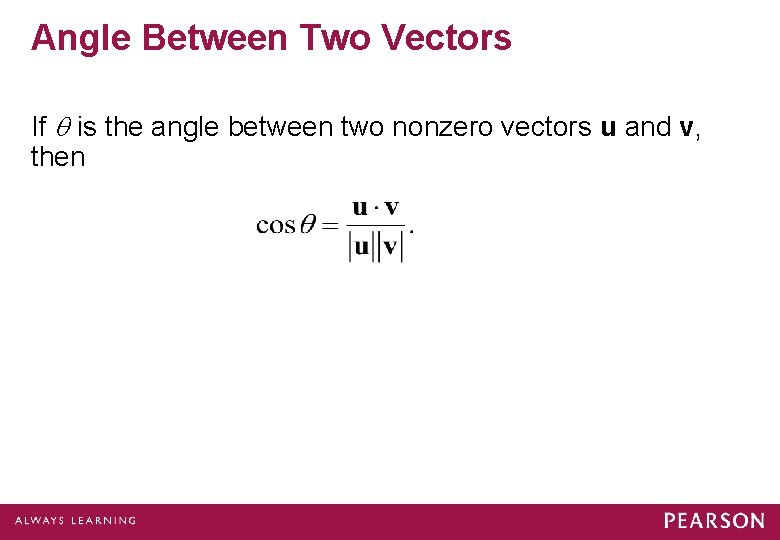
Angle Between Two Vectors If is the angle between two nonzero vectors u and v, then

Example Find the angle between Solution: Find u • v, |u| and |v|.

Forces in Equilibrium When several forces act through the same point on an object, their vector sum must be O in order for a balance to occur. When a balance occurs, then the object is either stationary or moving in a straight line without acceleration. The fact that the vector sum must be O for a balance, and vice versa, allows us to solve many applied problems involving forces.

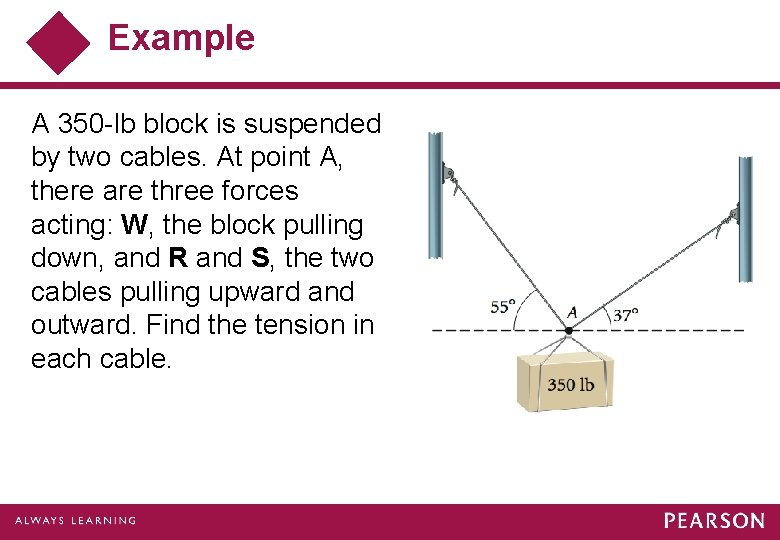
Example A 350 -lb block is suspended by two cables. At point A, there are three forces acting: W, the block pulling down, and R and S, the two cables pulling upward and outward. Find the tension in each cable.

Example (cont) Draw a force diagram.

Example (cont) Substitute R, S, and W into So we have two equations:

Example (cont) Solve equation 1 for |R|. Substitute this expression into equation 2. Solving this equation for |S|, we get |S| ≈ 201, and substituting 201 for |R| in the expression above, we get |R| ≈ 280. The tensions in the cables are 280 lb and 201 lb.