Section 8 4 Continuous Probability Models Special Topics

Section 8. 4 – Continuous Probability Models Special Topics

Types of Probability Distributions �When the values for outcomes only take whole number values, the probability model is called discrete. Discrete values can be counted. �An example of a discrete probability model is the number of heads which appear when two coins are flipped: Heads 0 1 2 3 4 Prob. 1/16 4/16 6/16 4/16 1/16 �Discrete probability models are shown in tables and all the probabilities exist only at the whole numbers – in other words P(3. 5) = 0.

Types of Probability Distributions �The other type of probability model is called continuous. Examples of a continuous setting include blood pressure readings, times to run a race, the height of 4 th graders. �Continuous values cannot be counted, since they don’t always consist of whole number values. �Continuous data must be measured. �Since a value in a continuous data set isn’t always a whole number, you can’t represent the model with a table. Instead, you use a geometric area model.

Theory behind Density Curves �Let’s say you have a random number generator and you program it to generate any number between 0 and one. �You can represent this geometrically with a number line that starts at zero and ends at one. �So, what mathematicians do is to make the number line into a square which is 1 x 1. That gives an area = 1 (just like probability!)

Theory behind Density Curves �Thus, any geometric figure which has an area equal to 1 is called a density curve. �When you “cut” up the density curve and calculate the areas of the pieces, you get numbers which are less than 1 (just like probability). �You cut up the density curve from bottom to top. �We will look at three density curves in this section – a uniform density curve, a normal density curve, and an irregular density curve. �We will look at a normal density curve tomorrow.

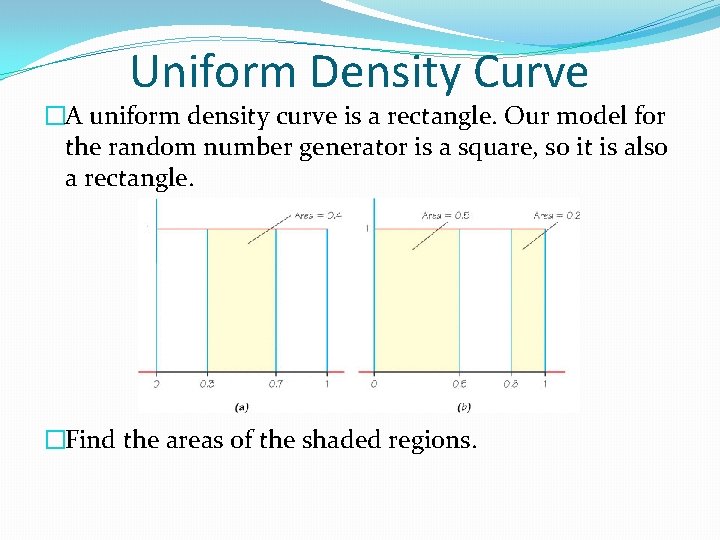
Uniform Density Curve �A uniform density curve is a rectangle. Our model for the random number generator is a square, so it is also a rectangle. �Find the areas of the shaded regions.

Uniform Density Curve �Caution: You can’t get probabilities for single numbers when the setting is continuous. This is because a single number would be represented with a line, and a line has NO area geometrically. �Thus, P(x =. 2) = 0

Irregular Density Curve �An irregular density curve is any geometric shape used for probability which isn’t a rectangle or bellshaped. �The area of the curve must be equal to 1. �The curve can be a triangle, trapezoid, etc. , or any combination of geometric shapes. �It, too, is cut up from bottom to top.

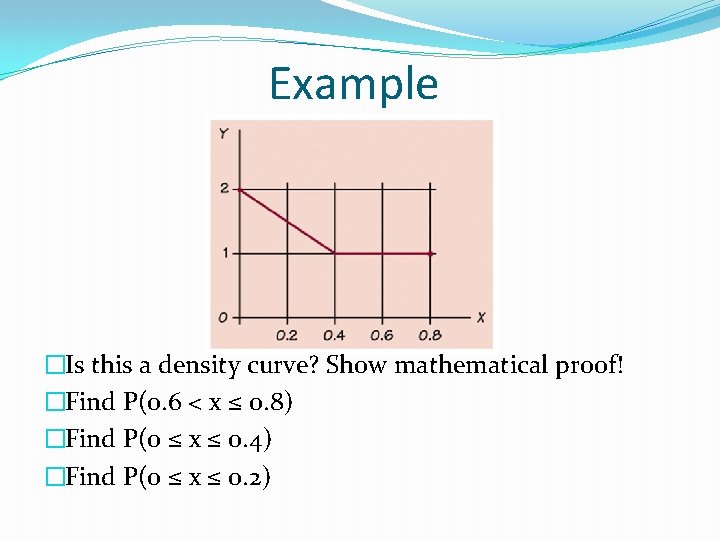
Example �Is this a density curve? Show mathematical proof! �Find P(0. 6 < x ≤ 0. 8) �Find P(0 ≤ x ≤ 0. 4) �Find P(0 ≤ x ≤ 0. 2)

Homework �Worksheet 8. 4 day 1.