Section 8 2 Basics of Hypothesis Testing Chapter

Section 8 -2 Basics of Hypothesis Testing

Chapter Learning Target: The main objective of this chapter is to develop the ability to conduct hypothesis tests for claims made about a population proportion p or a population mean .

Learning Targets This section presents individual components of a hypothesis test. We should know and understand the following: • How to identify the null hypothesis and alternative hypothesis from a given claim, and how to express both in symbolic form • How to calculate the value of the test statistic, given a claim and sample data • How to identify the critical value(s), given a significance level • How to identify the P-value, given a value of the test statistic • How to state the conclusion about a claim in simple and nontechnical terms

Quick Review & Preview �

Definitions In statistics, a hypothesis is a claim or statement about a property of a population. A hypothesis test (or test of significance) is a standard procedure for testing a claim about a property of a population.

Examples of Hypotheses that can be Tested Genetics: The Genetics & IVF Institute claims that its XSORT method allows couples to increase the probability of having a baby girl. Business: A newspaper headline makes the claim that most workers get their jobs through networking. Medicine: Medical researchers claim that when people with colds are treated with echinacea, the treatment has no effect.

Examples of Hypotheses that can be Tested Aircraft Safety: The Federal Aviation Administration claims that the mean weight of an airline passenger (including carry-on baggage) is greater than 185 lb, which it was 20 years ago. Quality Control: When new equipment is used to manufacture aircraft altimeters, the new altimeters are better because the variation in the errors is reduced so that the readings are more consistent. (In many industries, the quality of goods and services can often be improved by reducing variation. )

Examples of Hypotheses that can be Tested – One you might recognize… NFL: When a call is made on the field (such as a touchdown), but a “challenge” is made by the other coach to dispute the call made by the referee. Once a call is challenged, the play call is reviewed. The hypothesis would vary depending on the play in question. -- Similar circumstances now apply to other sports such as baseball, hockey, and tennis

Examples of Hypotheses that can be Tested – A few more… �A hypothesis is put forward that children who take vitamin C are less likely to become ill during flu season than those who do not. A hypothesis test is conducted where a sample group of children is given vitamin C for three months while another group is not. �Most redheads, a hypothesis suggests, are insecure about their hair color. A hypothesis test is conducted wherein redheads are given polygraph testing to determine how they feel about their hair color. �Hypothesis testing of the conception that people with obese parents are likely to become obese themselves suggests that obesity has little to do with genetics.

Rare Event Rule for Inferential Statistics If, under a given assumption, the probability of a particular observed event is exceptionally small, we conclude that the assumption is probably not correct.

Null Hypothesis: H 0 The null hypothesis (denoted by H 0) is a statement that the value of a population parameter (such as proportion or mean) is equal to some claimed value. We test the null hypothesis directly. Either reject H 0 or fail to reject H 0.

Alternative Hypothesis: H 1 The alternative hypothesis (denoted by H 1 or Ha or HA) is the statement that the parameter has a value that somehow differs from the null hypothesis. The symbolic form of the alternative hypothesis must use one of these symbols: , <, >. If the problem says phrases like: At least, No less than, Greater than or equal to Use: < If the problem says phrases like: At most, No more than, Less than or equal to Use: >

The P-Value Method

Example: A manager of an airline claims that the mean weight of airline passengers (including carry-on baggage) is at most 195 lb (the current value used by the Federal Aviation Administration). Identify the null hypothesis and the alternative hypothesis. H 0: w = 195 H 1: w > 195 Step 1: Express the given claim in symbolic form. The claim that the mean is at most 195 lb is expressed in symbolic form as ≤ 195 lb. Step 2: If ≤ 195 lb is false, then > 195 lb must be true. Step 3: Of the two symbolic expressions ≤ 195 lb and > 195 lb, we see that > 195 lb does not contain equality, so we let the alternative hypothesis H 1 be > 195 lb. Also, the null hypothesis must be a statement that the mean equals 195 lb, so we let H 0 be = 195 lb.

Example: An entomologist writes an article in a scientific journal which claims that fewer than 7 in ten thousand male fireflies are unable to produce light due to a genetic mutation. Use the parameter p, the true proportion of fireflies unable to produce light to identify the null hypothesis and the alternative hypothesis. H 0: p = 0. 0007 H 1: p < 0. 0007

Your Turn: A cereal company claims that the mean weight of the cereal in its packets is at least 14 oz. Identify the null hypothesis and the alternative hypothesis. H 0: w = 14 H 1: w < 14 A researcher claims that the amounts of acetaminophen in a certain brand of cold tablets have a mean different from the 3. 3 mg claimed by the manufacturer. Identify the null hypothesis and the alternative hypothesis. H 0: = 3. 3 H 1: 3. 3

Your Turn: A researcher claims that 81% of voters favor tax cuts. Identify the null hypothesis and the alternative hypothesis. H 0: p = 0. 81 H 1: p 0. 81

The P-Value Method

Setting the Significance Level

Examples

The P-Value Method

Test Statistic The test statistic is a value used in making a decision about the null hypothesis, and is found by converting the sample statistic to a score with the assumption that the null hypothesis is true.

Test Statistic - Formulas Test statistic for proportion Test statistic for mean Test statistic for standard deviation

Choosing the Test Statistic

Example: Let’s again consider the claim that the XSORT method of gender selection increases the likelihood of having a baby girl. Preliminary results from a test of the XSORT method of gender selection involved 14 couples who gave birth to 13 girls and 1 boy. Identify the hypothesis and use the given claim and the preliminary results to calculate the value of the test statistic. H 0: p = 0. 5, H 1: p > 0. 5.

Example: The claim is that the proportion of drowning deaths of children attributable to beaches is more than 0. 25, and the sample statistics include n = 681 drowning deaths of children with 30% of them attributable to beaches. Identify the claim and use the preliminary results to calculate the value of the test statistic. H 0: p = 0. 25, H 1: p > 0. 25.

Your Turn: The claim is that the proportion of peas with yellow pods is equal to 0. 35. The sample statistics from one of Mendel’s experiments include 580 peas with 192 of them having yellow pods. Use the given claim and the preliminary results to calculate the value of the test statistic. H 0: p = 0. 35, H 1: p 0. 35.

Homework P. 409: Hypotheses: 9 -13 Test Statistic: 27

The P-Value Method

P-Values

P-Value The P-value (or p-value or probability value) is the probability of getting a value of the test statistic that is at least as extreme as the one representing the sample data, assuming that the null hypothesis is true. Critical region in the left tail: P-value = area to the left of the test statistic Critical region in the right tail: P-value = area to the right of the test statistic Critical region in two tails: P-value = twice the area in the tail beyond the test statistic

P-Value The null hypothesis is rejected if the P-value is very small, such as 0. 05 or less. Here is a memory tool useful for interpreting the P-value: If the P is low, the null must go. If the P is high, the null will fly.

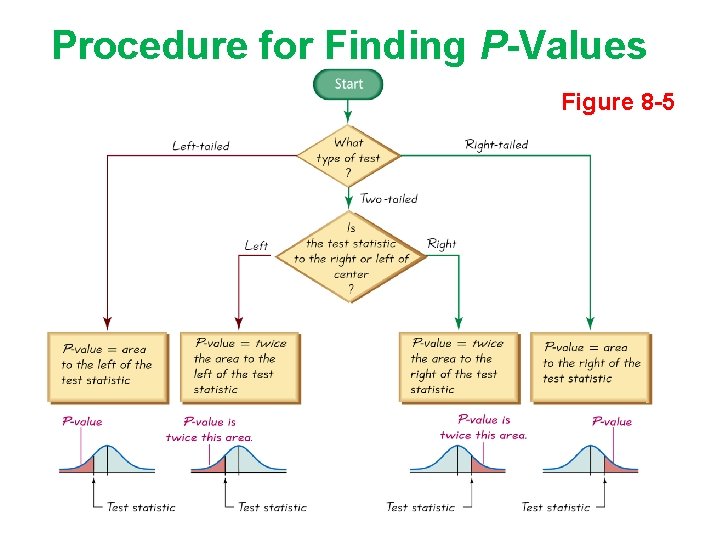
Procedure for Finding P-Values Figure 8 -5

Caution Don’t confuse a P-value with a proportion p. Know this distinction: P-value = probability of getting a test statistic at least as extreme as the one representing sample data p = population proportion

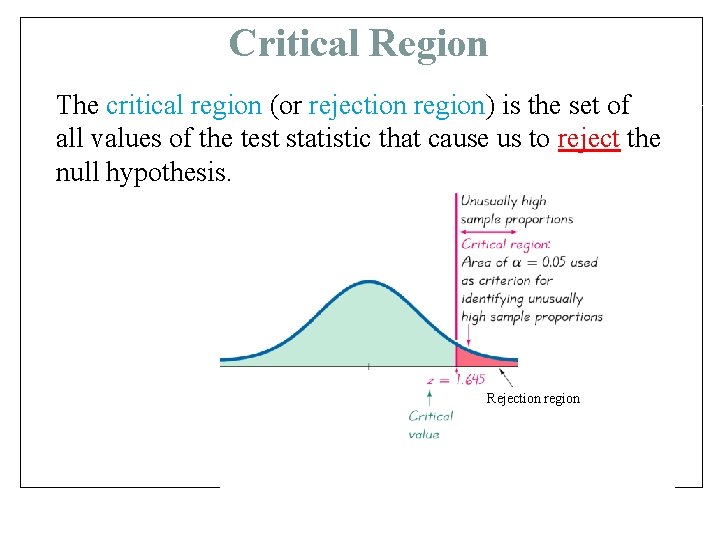
Critical Region The critical region (or rejection region) is the set of all values of the test statistic that cause us to reject the null hypothesis. Rejection region

Significance Level The significance level (denoted by ) is the probability that the test statistic will fall in the critical region when the null hypothesis is actually true. This is the same introduced in Section 7 -2. Common choices for are 0. 05, 0. 01, and 0. 10.

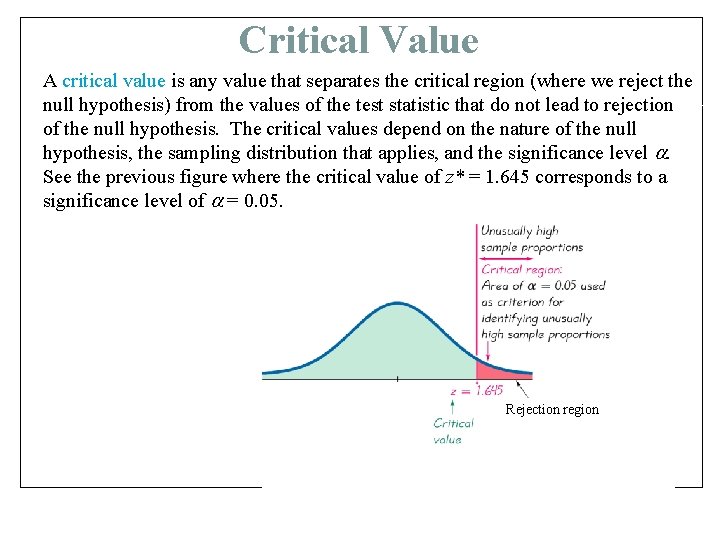
Critical Value A critical value is any value that separates the critical region (where we reject the null hypothesis) from the values of the test statistic that do not lead to rejection of the null hypothesis. The critical values depend on the nature of the null hypothesis, the sampling distribution that applies, and the significance level . See the previous figure where the critical value of z* = 1. 645 corresponds to a significance level of = 0. 05. Rejection region

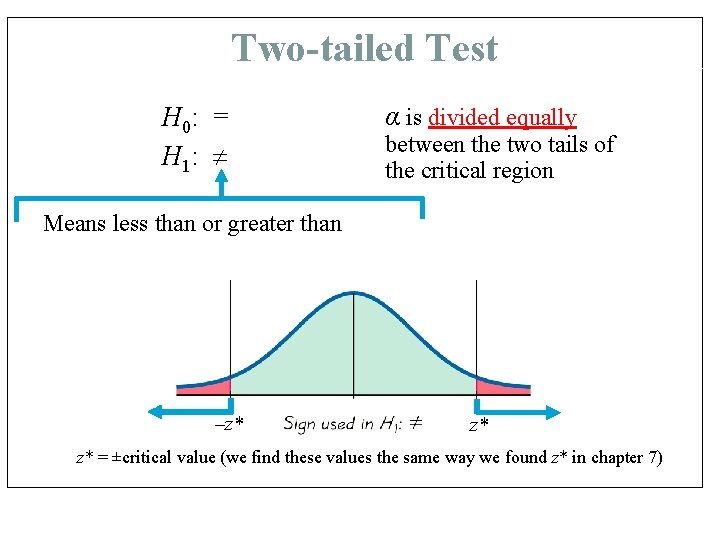
Two-tailed Test H 0: = H 1: α is divided equally between the two tails of the critical region Means less than or greater than –z* z* z* = ±critical value (we find these values the same way we found z* in chapter 7)

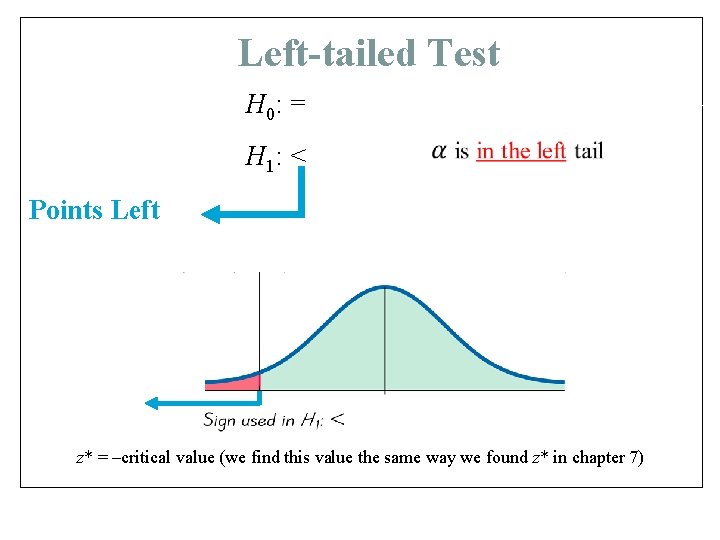
Left-tailed Test H 0: = H 1: < Points Left z* = –critical value (we find this value the same way we found z* in chapter 7)

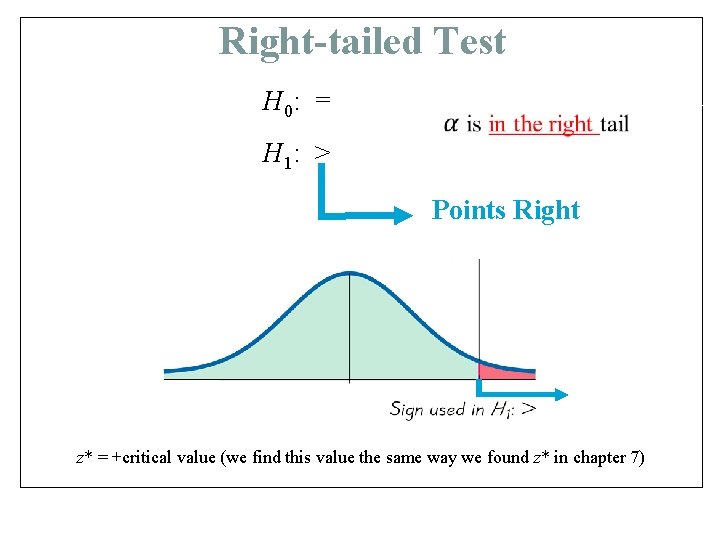
Right-tailed Test H 0: = H 1: > Points Right z* = +critical value (we find this value the same way we found z* in chapter 7)

P-Value The P-value (or p-value or probability value) is the probability of getting a value of the test statistic that is at least as extreme as the one representing the sample data, assuming that the null hypothesis is true.

P-Value Critical region in the left tail: P-value = area to the left of the test statistic On Calculator: normalcdf (– 999999, a, 0, 1) a

P-Value Critical region in the right tail: P-value = area to the right of the test statistic On Calculator: normalcdf (a, 999999, 0, 1) a

P-Value Critical region in the two tail: P-value = Twice the area in the tail beyond the test statistic **In other words, DOUBLE your P-value a On Calc: normalcdf (– 999999, a, 0, 1) a On Calc: normalcdf (a, 999999, 0, 1)

Example Consider the claim that with the XSORT method of gender selection, the likelihood of having a baby girl is different from p = 0. 5, or p 0. 5 (two-tailed). The test statistic is z = 3. 2071. First determine whether the given conditions result in a critical region in the two tails, then use calculator to find the P-value. Interpret the P-value. Using calculator to find that the area to the right of z = 3. 2071 is 0. 0007. In this case, the P-value is twice the area to the right of the test statistic, so we have: P-Value = 2 0. 0007 = 0. 0014 0. 0007 3. 2071

Example The P-value is 0. 0014 (or 0. 0013 if greater precision is used for the calculations). The small P-value of 0. 0014 shows that there is a very small chance of getting the sample results that led to a test statistic of z = 3. 2071. This suggests that with the XSORT method of gender selection, the likelihood of having a baby girl is different from 0. 5.

Example Given that our test statistic is z = 3. 2071 for the Microsort problem (remember that the alternative hypothesis is p > 0. 5). What is the p-value? The test statistic follows the normal distribution, we need to look at the area at the right tail of the distribution that test statistic cuts. To find the area, normalcdf(3. 2071, 9999, 0, 1) » 0. 00067 P-value = 0. 00067 z = 3. 2071

The P-Value Method

Types of Hypothesis Tests: Two-tailed, Left-tailed, Right-tailed The tails in a distribution are the extreme regions bounded by critical values. Determinations of P-values and critical values are affected by whether a critical region is in two tails, the left tail, or the right tail. It therefore becomes important to correctly characterize a hypothesis test as two-tailed, left-tailed, or right-tailed.

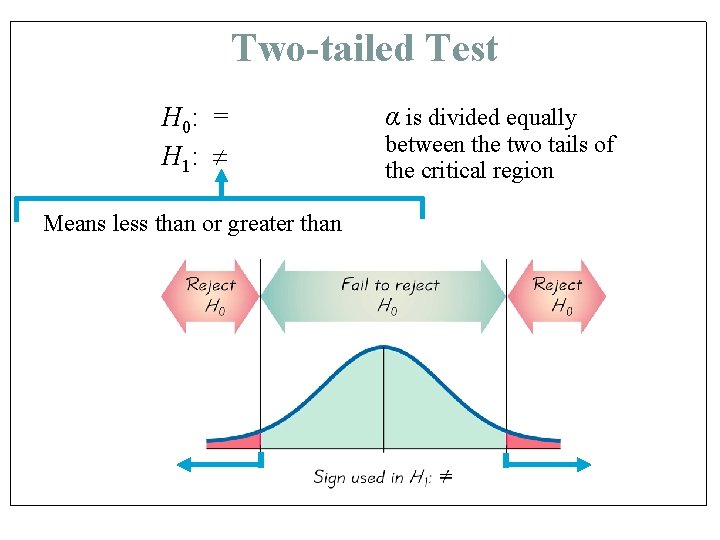
Two-tailed Test H 0: = H 1: Means less than or greater than α is divided equally between the two tails of the critical region

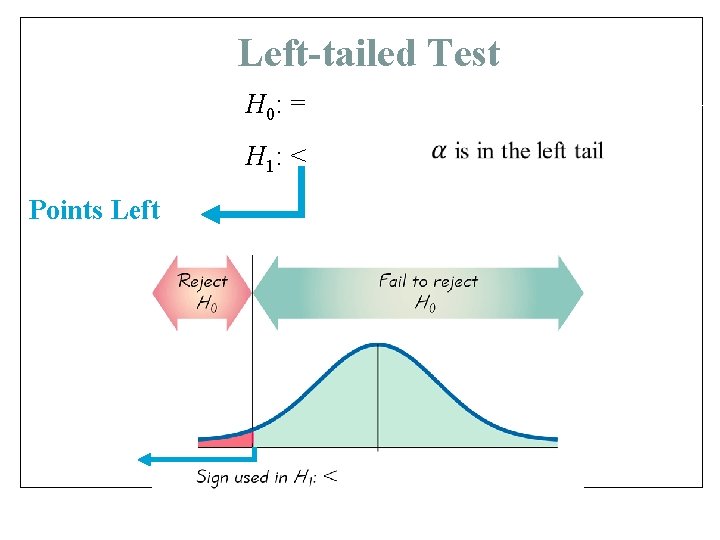
Left-tailed Test H 0: = H 1: < Points Left

Right-tailed Test H 0: = H 1: > Points Right

P-Value The null hypothesis is rejected if the P-value is very small, such as 0. 05 or less. Here is a memory tool useful for interpreting the Pvalue: If the P is low, the null must go. If the P is high, the null will fly.

Caution Don’t confuse a P-value with a proportion p. Know this distinction: P-value = probability of getting a test statistic at least as extreme as the one representing sample data p = population proportion

Example: Use the given information to find the P-value. The test statistic in a right-tailed test is z = 1. 57 at = 0. 05. Right-Tailed Test P-Value = normalcdf(1. 57, 9999, 0, 1) 0. 0582 > 0. 05, fail to reject H 0. Example: Use the given information to find the P-value. The test statistic in a left-tailed test is z = – 1. 84 at = 0. 05. Left-Tailed Test P-Value = normalcdf(-9999, -1. 84, 0, 1) 0. 0329 < 0. 05, reject H 0. Example: Use the given information to find the P-value. The test statistic in a two-tailed test is z = – 1. 76. at = 0. 05. Two-Tailed Test P-Value = 2 x normalcdf(-9999, -1. 76, 0, 1) 2 x 0. 0392 = 0. 0784 > 0. 05, fail to reject H 0.

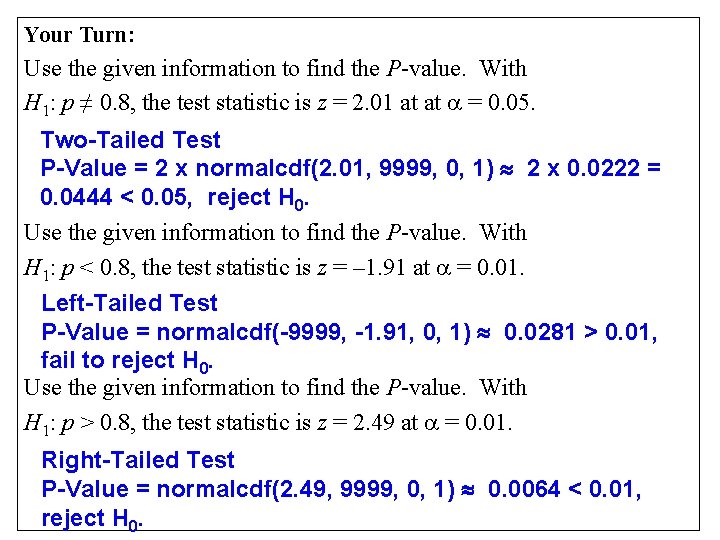
Your Turn: Use the given information to find the P-value. With H 1: p ≠ 0. 8, the test statistic is z = 2. 01 at at = 0. 05. Two-Tailed Test P-Value = 2 x normalcdf(2. 01, 9999, 0, 1) 2 x 0. 0222 = 0. 0444 < 0. 05, reject H 0. Use the given information to find the P-value. With H 1: p < 0. 8, the test statistic is z = – 1. 91 at = 0. 01. Left-Tailed Test P-Value = normalcdf(-9999, -1. 91, 0, 1) 0. 0281 > 0. 01, fail to reject H 0. Use the given information to find the P-value. With H 1: p > 0. 8, the test statistic is z = 2. 49 at = 0. 01. Right-Tailed Test P-Value = normalcdf(2. 49, 9999, 0, 1) 0. 0064 < 0. 01, reject H 0.

The P-Value Method

Wording of Final Conclusion Figure 8 -7

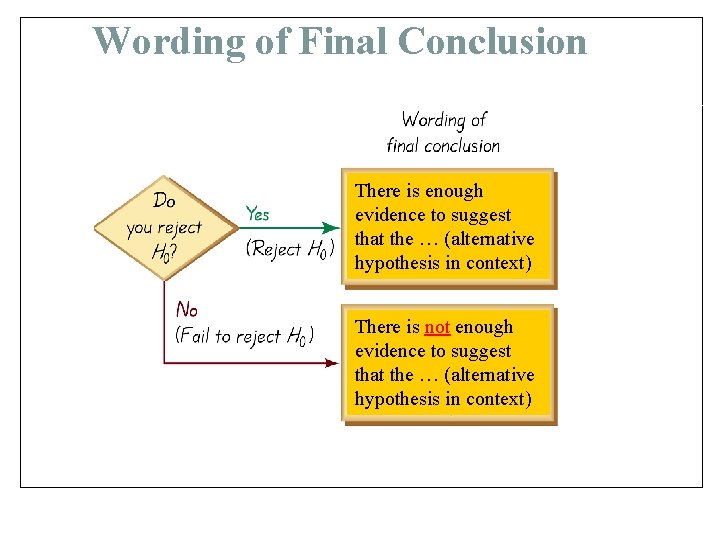
Wording of Final Conclusion There is enough evidence to suggest that the … (alternative hypothesis in context) There is not enough evidence to suggest that the … (alternative hypothesis in context)

Conclusions in Hypothesis Testing By using the P-Value Method at the significance level , we always test the null hypothesis. The initial conclusion will always be one of the following based on the P-Value: 1. If P-Value , reject the null hypothesis. 2. If P-value > , fail to reject the null hypothesis.

Example: State the final conclusion in simple nontechnical terms. Original claim: The percentage of blue M&Ms is greater than 5%. Initial conclusion: Fail to reject the null hypothesis. There is not sufficient sample evidence to support the claim that the percentage of blue M&Ms is greater than 5%.

Example: An entomologist writes an article in a scientific journal which claims that fewer than 12 in ten thousand male fireflies are unable to produce light due to a genetic mutation. Assuming that a hypothesis test of the claim has been conducted and that the conclusion is to reject the null hypothesis, state the conclusion in nontechnical terms. The sample data support the claim that fewer than 12 in ten thousand male fireflies are unable to produce light due to a genetic mutation.

Your Turn: State the final conclusion in simple nontechnical terms. Alternative hypothesis(Original claim): The percentage of Americans who know their credit score is not equal to 20%. Initial conclusion: fail to reject the null hypothesis. There is not sufficient sample evidence to support the claim that the percentage of Americans who know their credit score is not equal to 20%.

Example Since P-Value = 0. 0007 < 0. 05, so we are able to reject the null hypothesis. If the original test is one tail, then the P-Value = 0. 03 < 0. 05, so we are able to reject the null hypothesis. If the original test is two tails, then the P-Value = 0. 03 * 2 = 0. 06 > 0. 05, we will not be able to reject the null hypothesis.

Recap In this section we have discussed: v Null and alternative hypotheses. v Test statistics. v Significance levels. v P-values. v Decision criteria. v Type I and II errors. v Power of a hypothesis test.

One Final Meme

Homework P. 409: P-Value/Reject: 33 -36 Conclusion: 38 -39