SECTION 7 6 ROTATIONS AND ROTATIONAL SYMMETRY ROTATIONS

  • Slides: 9
Download presentation
SECTION 7. 6 ROTATIONS AND ROTATIONAL SYMMETRY

SECTION 7. 6 ROTATIONS AND ROTATIONAL SYMMETRY

ROTATIONS There are two types of rotations: � CW – Clockwise � CCW CW

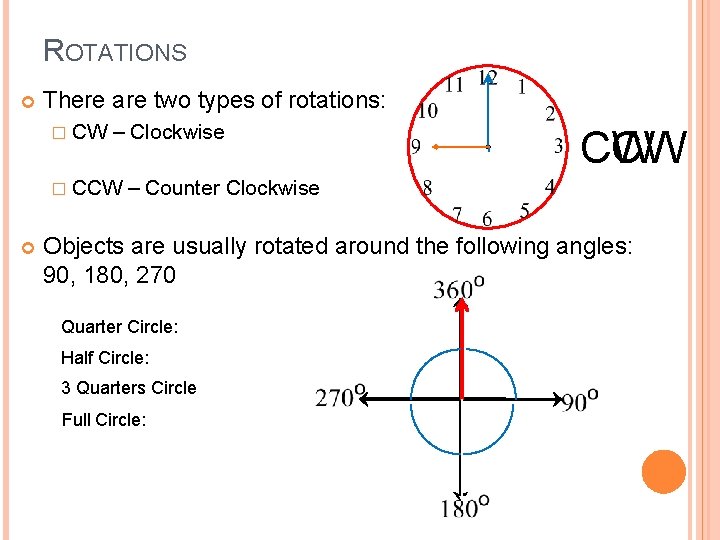
ROTATIONS There are two types of rotations: � CW – Clockwise � CCW CW – Counter Clockwise Objects are usually rotated around the following angles: 90, 180, 270 Quarter Circle: Half Circle: 3 Quarters Circle Full Circle:

WINDMILL METHOD: When asked to rotate a point about the origin by 90, 180,

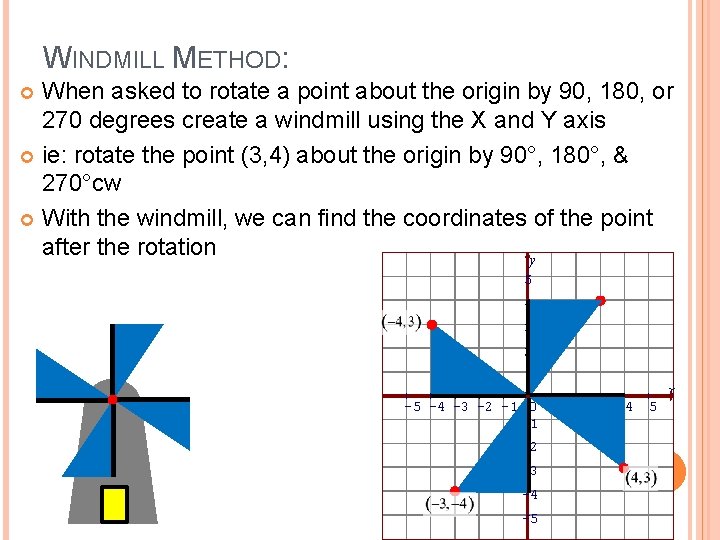
WINDMILL METHOD: When asked to rotate a point about the origin by 90, 180, or 270 degrees create a windmill using the X and Y axis ie: rotate the point (3, 4) about the origin by 90°, 180°, & 270°cw With the windmill, we can find the coordinates of the point after the rotation y 5 4 3 2 1 -5 -4 -3 -2 -1 0 1 -1 -2 -3 -4 -5 x 2 3 4 5

Practice: Given the point P(-2, 4) i) Rotate it 90° ccw about the origin

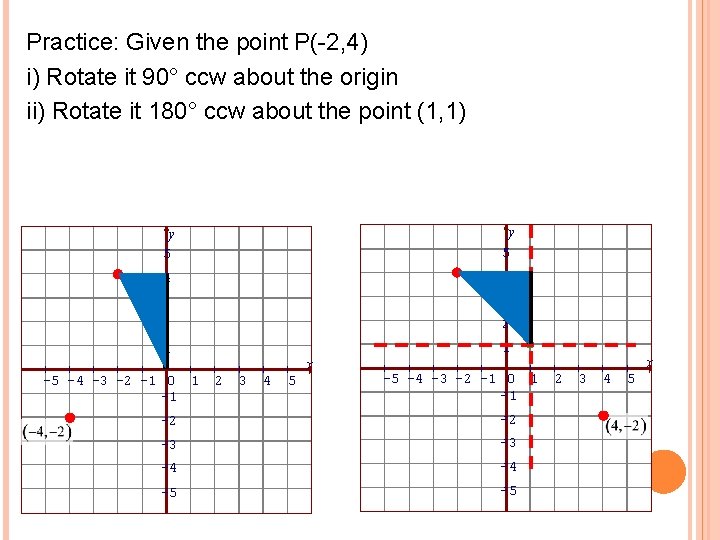
Practice: Given the point P(-2, 4) i) Rotate it 90° ccw about the origin ii) Rotate it 180° ccw about the point (1, 1) y 5 4 4 3 3 2 2 1 1 -5 -4 -3 -2 -1 0 1 -1 x 2 3 4 5 -5 -4 -3 -2 -1 0 1 -1 -2 -2 -3 -3 -4 -4 -5 -5 x 2 3 4 5

EX: GIVEN THE FOLLOWING OBJECT, ROTATE IT 90⁰ (CW) ABOUT THE ORIGIN AND FIND

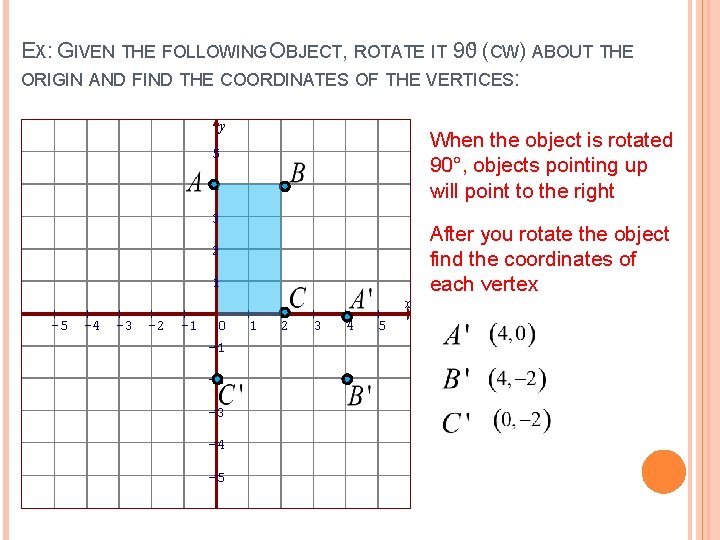
EX: GIVEN THE FOLLOWING OBJECT, ROTATE IT 90⁰ (CW) ABOUT THE ORIGIN AND FIND THE COORDINATES OF THE VERTICES: y When the object is rotated 90°, objects pointing up will point to the right 5 4 3 2 1 x -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 3 4 5 After you rotate the object find the coordinates of each vertex

PRACTICE: GIVEN THE FOLLOWING OBJECTS, FIND THE COORDINATES OF THE VERTEX AFTER EACH ROTATION:

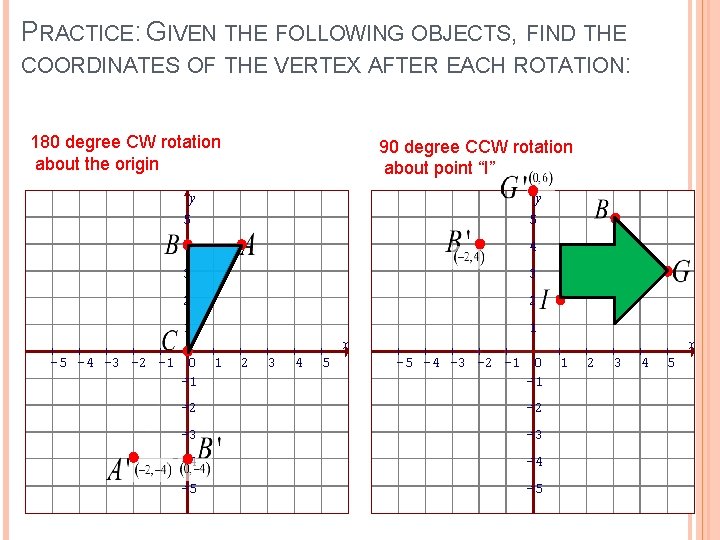
PRACTICE: GIVEN THE FOLLOWING OBJECTS, FIND THE COORDINATES OF THE VERTEX AFTER EACH ROTATION: 180 degree CW rotation about the origin 90 degree CCW rotation about point “I” y y 5 5 4 4 3 3 2 2 1 1 x -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 x -5 -4 -3 -2 -1 0 -1 -2 -2 -3 -3 -4 -4 -5 -5 1 2 3 4 5

ROTATIONAL SYMMETRY Objects can be rotated such that it will look the same A

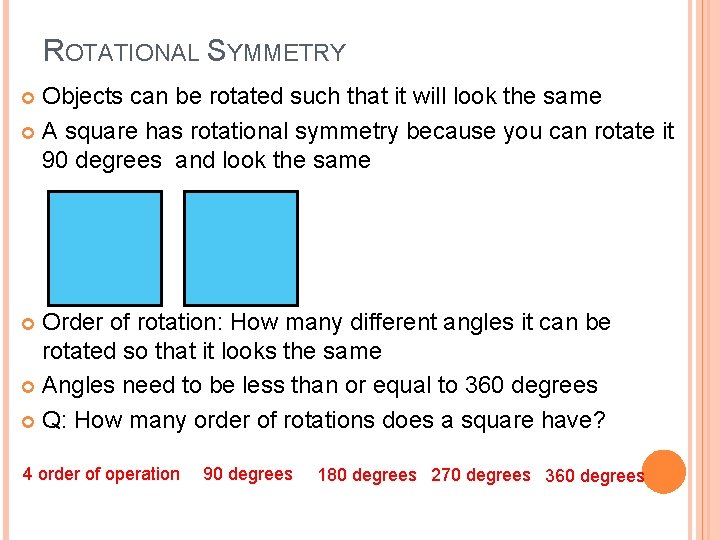
ROTATIONAL SYMMETRY Objects can be rotated such that it will look the same A square has rotational symmetry because you can rotate it 90 degrees and look the same Order of rotation: How many different angles it can be rotated so that it looks the same Angles need to be less than or equal to 360 degrees Q: How many order of rotations does a square have? 4 order of operation 90 degrees 180 degrees 270 degrees 360 degrees

EX: WHICH OF THE FOLLOWING HAVE ROTATIONAL SYMMETRY? IF YES, INDICATE THE ORDER OF

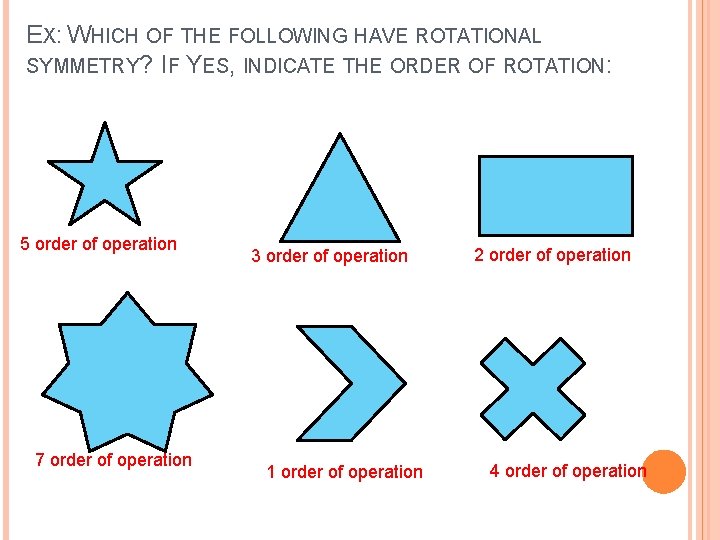
EX: WHICH OF THE FOLLOWING HAVE ROTATIONAL SYMMETRY? IF YES, INDICATE THE ORDER OF ROTATION: 5 order of operation 7 order of operation 3 order of operation 1 order of operation 2 order of operation 4 order of operation

HOMEWORK: P 366 # 4 – 6, 8 – 10, 13 – 14

HOMEWORK: P 366 # 4 – 6, 8 – 10, 13 – 14