Section 7 1 Introduction to Function Relation A

Section 7. 1 Introduction to Function

Relation • A connection between two things, input and output. • Examples of relations are school and study family and siblings sports and hockey • As you can see there are many words that can describe the first word. What ideas do you have?

Formal Definition for Relation • Relation – A connection between two things – A pairing of elements of one set with elements of a second set. • The one set and second set have proper algebra terms. – One set is referred to as the domain. – Second set is referred to as the range. – A set of ordered pairs

Example: Which are Relations? • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Which are Relations • They are ALL Relations

Special types of Relations • Function • One – to – One Function • These are special because there is a unique connection between the input (domain) and the output (range) • We will have different definitions for function and one – to – one function

Function • A relation in which each element of the domain is paired to exactly one element in the range • Given an equation you COULD see f(x) • Given a graph a function will pass the Vertical Line Test (VLT) – Vertical Line Test = if you can draw vertical lines on your graph and only pass through one point on the graph then your graph is a function.

Example: Which are Functions? • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Example: Which are Functions? • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} F B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F F(x) = 2 x – 5 F Y = x² + 5 graph the equation F • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

One – to – One Function • A function in which each element of the range is paired to exactly one element in the domain. • No special indication for an equation. • Must pass the Vertical Line Test AND the Horizontal Line Test

Example: Which are 1 -1 Functions? • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Example: Which are 1 -1 Functions? • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} 1 -1 B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 1 -1 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Domain / Range • Domain – Given an ordered pair (x, y) the first element, the input, the x element, the values on the horizontal line are all referred to as the domain. • Range – Given an ordered pair (x, y) the second element, the output, the y element, the values on the vertical line are all referred to as the range.

Example: Define the Domain • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Example: Define the Range • • • A = {(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1)} B = {(1, 5), (-2, 3/2), (0, 2), (-2, 4), (-1/5, 0)} C = {(-1, 2), (1/3, -2), (5, -2), (1/3, 2), (0, -1/9)} F(x) = 2 x – 5 Y = x² + 5 • • • Red Green Gold Blue White Bakersfield condors Money Cal Poly Bakersfield College USA Flag

Evaluating a Function • Evaluating a function either has you – Substitute values • Given a function and a value. • Substitute value in for proper variable. • Solve for other variable. – Play with a graph • • • Given a graph and a value. Find that value on the correct axis. Find the connection of that value and the given graph Connect that point to the other axis. Find the new value.

Evaluating a function • Given f(x) = x² - 2 x + 3 Evaluate – f(-3) • f(-3) = (-3)² - 2(-3) + 3 • f(-3) = 9 + 6 + 3 =18 – f(2) – f(0) – f(-5) – f(1/2)

Evaluating a function • Given H(t) = t – 12 evaluate – H(y) – H(y + 2) – H(2 y) – H(y) +2

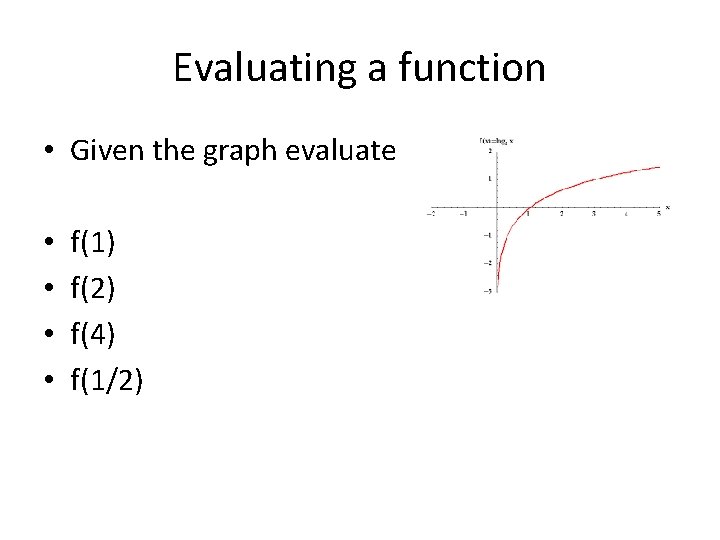
Evaluating a function • Given the graph evaluate • • f(1) f(2) f(4) f(1/2)

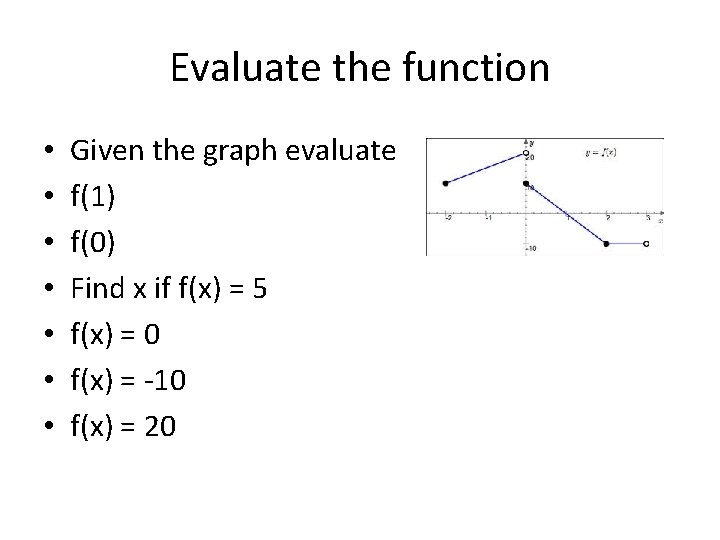
Evaluate the function • • Given the graph evaluate f(1) f(0) Find x if f(x) = 5 f(x) = 0 f(x) = -10 f(x) = 20

Homework • 7. 1 – # 9, 16, 27, 31, 33, 37, 38, 40, 43, 46, 47, 57