Section 7 1 1 Discrete and Continuous Random

Section 7. 1. 1 Discrete and Continuous Random Variables AP Statistics, Section 7. 1, Part 1

Random Variables n n n A random variable is a variable whose value is a numerical outcome of a random phenomenon. For example: Flip three coins and let X represent the number of heads. X is a random variable. We usually use capital letters to denotes random variables. The sample space S lists the possible values of the random variable X. We can use a table to show the probability distribution of a discrete random variable. AP Statistics, Section 7. 1, Part 1 2

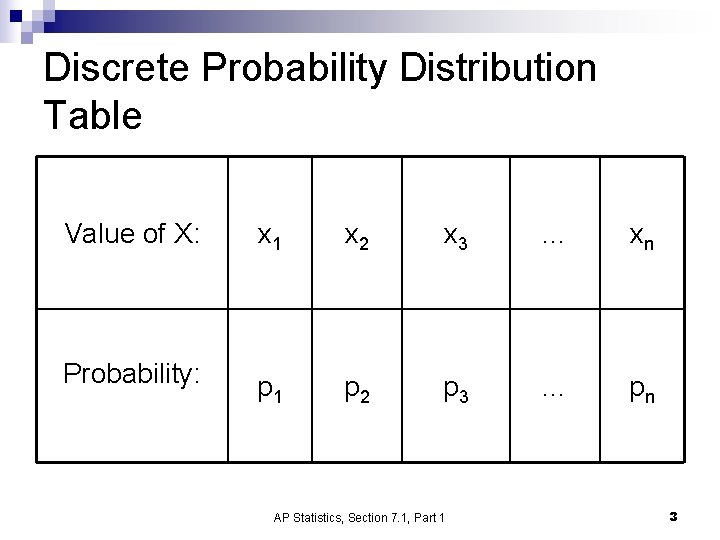
Discrete Probability Distribution Table Value of X: x 1 x 2 x 3 … xn Probability: p 1 p 2 p 3 … pn AP Statistics, Section 7. 1, Part 1 3

Discrete Random Variables n A discrete random variable X has a countable number of possible values. The probability distribution of X lists the values and their probabilities. X: x 1 x 2 x 3 … xk P(X): p 1 p 2 p 3 … pk 1. 0 ≤ pi ≤ 1 2. p 1 + p 2 + p 3 +… + pk = 1. AP Statistics, Section 7. 1, Part 1 4

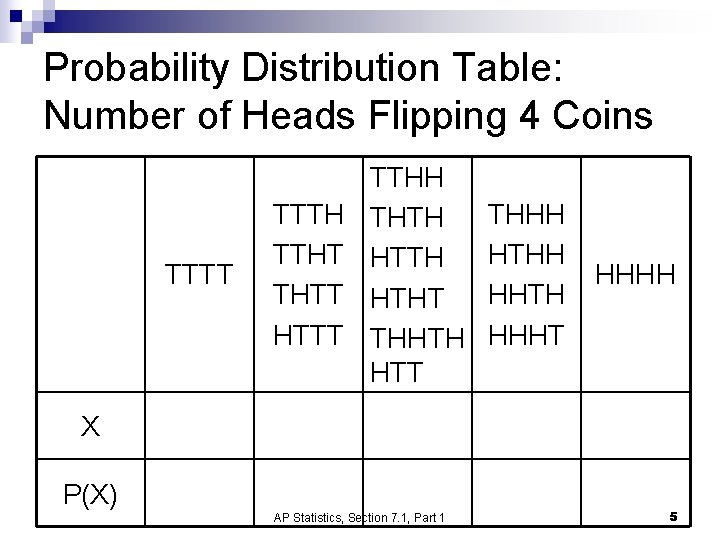
Probability Distribution Table: Number of Heads Flipping 4 Coins TTTT TTTH TTHT THTT HTTT TTHH THTH HTHT THHTH HTT THHH HTHH HHTH HHHT HHHH X 0 1 2 3 4 P(X) 1/16 4/16 6/16 4/16 1/16 AP Statistics, Section 7. 1, Part 1 5

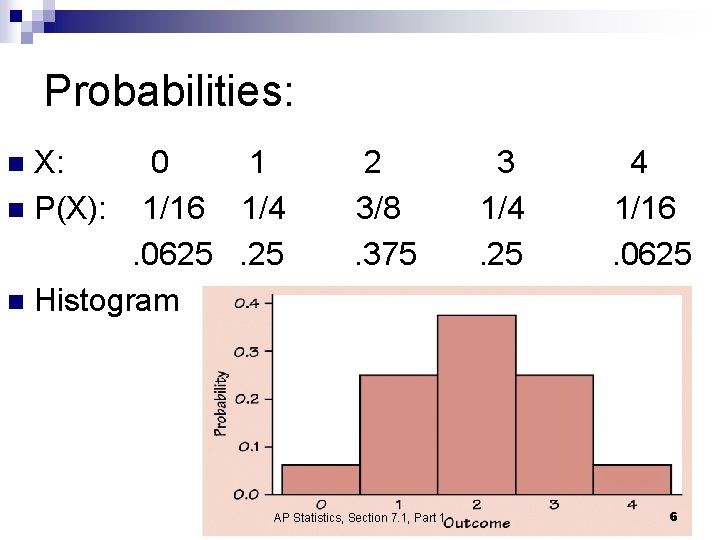
Probabilities: X: n P(X): 0 1 1/16 1/4. 0625. 25 n Histogram n 2 3/8. 375 AP Statistics, Section 7. 1, Part 1 3 1/4. 25 4 1/16. 0625 6

Questions. n n Using the previous probability distribution for the discrete random variable X that counts for the number of heads in four tosses of a coin. What are the probabilities for the following? P(X = 2). 375 +. 25 +. 0625 =. 6875 P(X ≥ 2) 1 -. 0625 =. 9375 P(X ≥ 1) AP Statistics, Section 7. 1, Part 1 7

What is the average number of heads? AP Statistics, Section 7. 1, Part 1 8

Continuous Random Varibles Suppose we were to randomly generate a decimal number between 0 and 1. There are infinitely many possible outcomes so we clearly do not have a discrete random variable. n How could we make a probability distribution? n We will use a density curve, and the probability that an event occurs will be in terms of area. n AP Statistics, Section 7. 1, Part 1 9

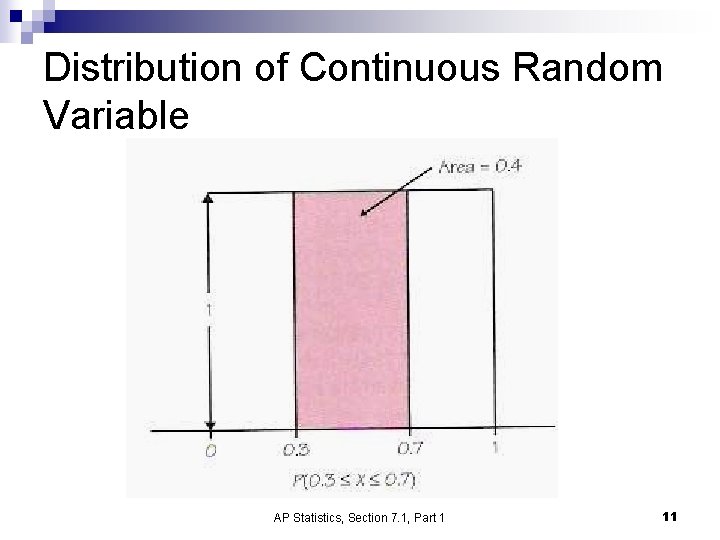
Definition: A continuous random variable X takes all values in an interval of numbers. n The probability distribution of X is described by a density curve. The Probability of any event is the area under the density curve and above the values of X that make up the event. n All continuous random distributions assign probability 0 to every individual outcome. n AP Statistics, Section 7. 1, Part 1 10

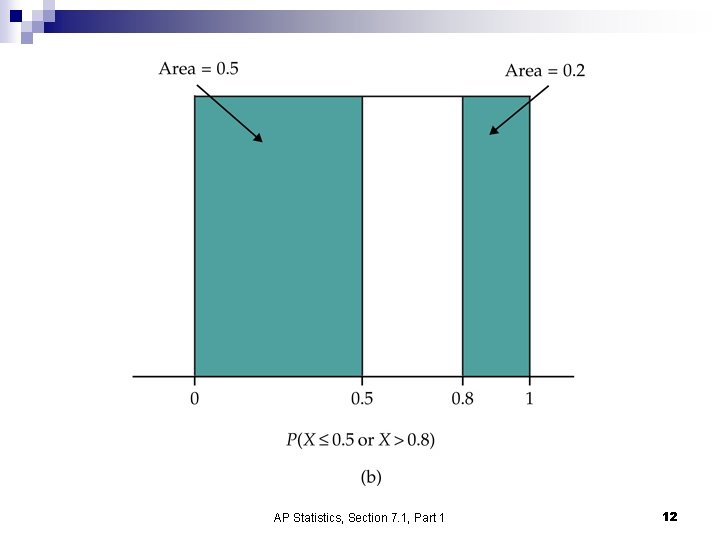
Distribution of Continuous Random Variable AP Statistics, Section 7. 1, Part 1 11

AP Statistics, Section 7. 1, Part 1 12

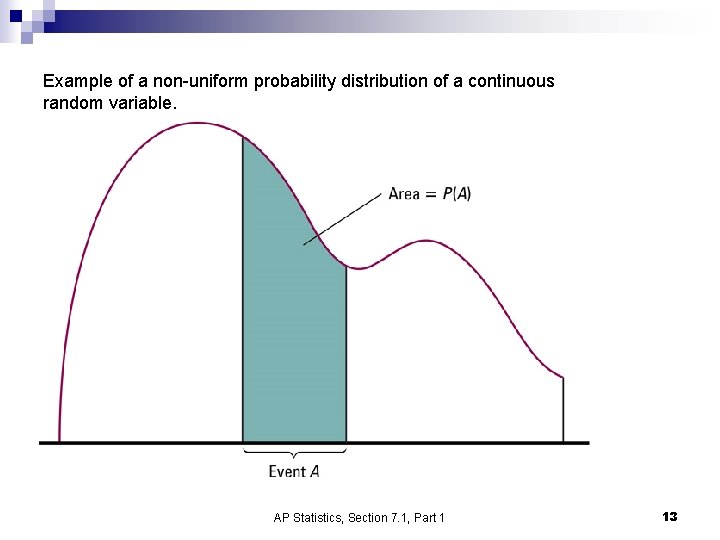
Example of a non-uniform probability distribution of a continuous random variable. AP Statistics, Section 7. 1, Part 1 13

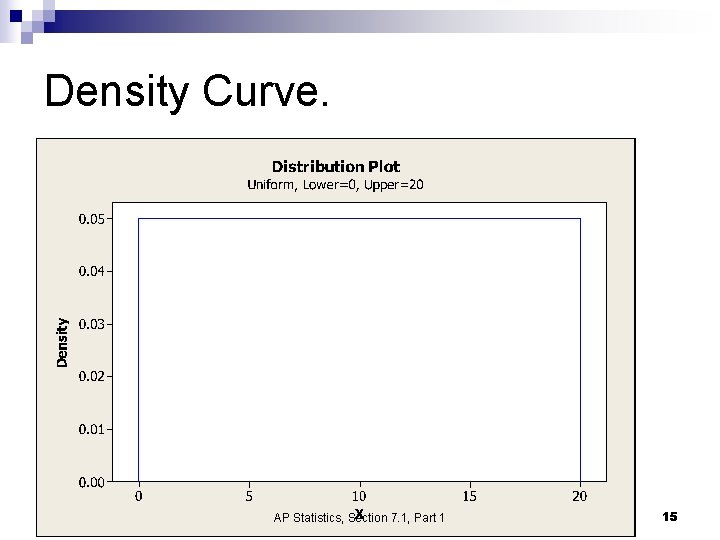
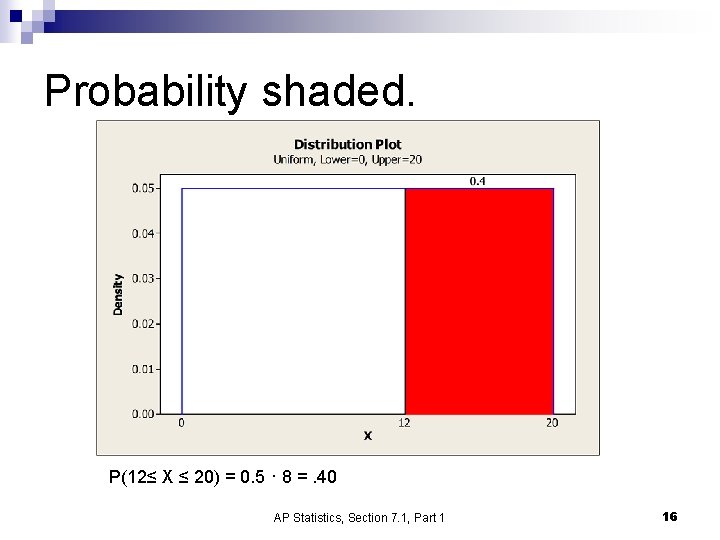
Problem Let X be the amount of time (in minutes) that a particular San Francisco commuter must wait for a BART train. Suppose that the density curve is a uniform distribution. n Draw the density curve. n What is the probability that the wait is between 12 and 20 minutes? n AP Statistics, Section 7. 1, Part 1 14

Density Curve. AP Statistics, Section 7. 1, Part 1 15

Probability shaded. P(12≤ X ≤ 20) = 0. 5 · 8 =. 40 AP Statistics, Section 7. 1, Part 1 16

Normal Curves n n n We’ve studied a density curve for a continuous random variable before with the normal distribution. Recall: N(μ, σ) is the normal curve with mean μ and standard deviation σ. If X is a random variable with distribution N(μ, σ), then is N(0, 1) AP Statistics, Section 7. 1, Part 1 17

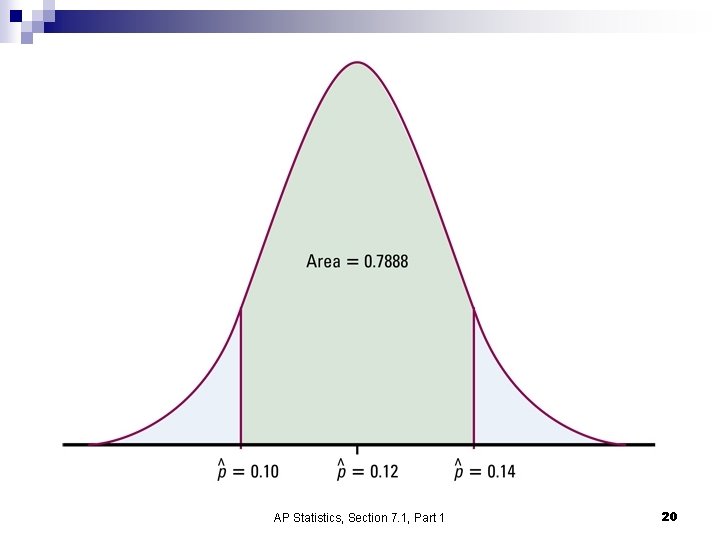
Example n n Students are reluctant to report cheating by other students. A sample survey puts this question to an SRS of 400 undergraduates: “You witness two students cheating on a quiz. Do you go to the professor and report the cheating? ” Suppose that if we could ask all undergraduates, 12% would answer “Yes. ” The proportion p = 0. 12 would be a parameter for the population of all undergraduates. AP Statistics, Section 7. 1, Part 1 18

Example continued n n n Students are reluctant to report cheating by other students. A sample survey puts this question to an SRS of 400 undergraduates: “You witness two students cheating on a quiz. Do you go to the professor and report the cheating? ” What is the probability that the survey results differs from the truth about the population by more than 2 percentage points? Because p = 0. 12, the survey misses by more than 2 percentage points if AP Statistics, Section 7. 1, Part 1 19

AP Statistics, Section 7. 1, Part 1 20

Example continued Calculations About 21% of sample results will be off by more than two percentage points. AP Statistics, Section 7. 1, Part 1 21

Summary n n A discrete random variable X has a countable number of possible values. The probability distribution of X lists the values and their probabilities. A continuous random variable X takes all values in an interval of numbers. The probability distribution of X is described by a density curve. The Probability of any event is the area under the density curve and above the values of X that make up the event. AP Statistics, Section 7. 1, Part 1 22

Summary When you work problems, first identify the variable of interest. n X = number of _____ for discrete random variables. n X = amount of _____ for continuous random variables. n AP Statistics, Section 7. 1, Part 1 23